Nicht immer passt wirklich alles zusammen
Auf dem bekannten Klimablog WUWT (Whats Up With That) macht sich Willis Eschenbach unter dem Titel “Can A Cold Object Warm A Hot Object?“ Gedanken darüber, ob ein kalter Körper einen warmen Körper erwärmen kann. Ziel des Artikels ist es offenbar, das Modell einer sogenannten atmosphärischen Gegenstrahlung zu stützen.
Zunächst kommt Eschenbach anhand des in Abbildung 1 dargestellten Beispiels mit Geldflüssen auf den durchaus nachvollziehbaren Ansatz, die Nettoströme zu betrachten. Seiner dort dargestellten Logik zufolge sagt der zweite Hauptsatz der Thermodynamik nichts über die Einzelflüsse aus, sondern nur über den resultierenden Nettofluss. Im übertragenen Sinne verliert nach dem Modell von Eschenbach der Körper mit der höheren Temperatur also immer mehr Energie, als er im gleichen Zeitraum von einem kälteren Körper zugeliefert bekommt.
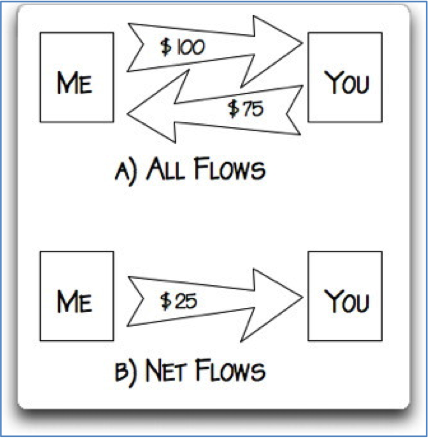
Bild: Willis Eschenbach
Abbildung 1: Das Beispiel von Eschenbach @ WUWT
Der warme Körper kann also durch das Zuliefern von Energie durch einen kälteren Körper nicht wärmer werden, als er schon ist, er kühlt nur weniger langsam ab. Das kann man sich anhand von 2 Tassen heißen Kaffee deutlich machen, eine Tasse lassen wir in der Küche stehen und die andere stellen wir auf die winterliche Terrasse. Im Ergebnis wird die Tasse in der Küche länger warm bleiben, als die auf der Terrasse. Beides ist über die Umgebungstemperatur leicht erklärbar.
Soweit, so gut – und auch noch nachvollziehbar, und damit wäre bisher der 2. Hauptsatz der Thermodynamik erfüllt.
Dann aber wird es ziemlich unübersichtlich, denn plötzlich kommt Eschenbach mit der Idee, ein kalter Körper konnte einen noch kälteren Körper hinter sich verbergen, also dafür sorgen, dass ein warmer Körper nicht in dem Maße abkühlt, wie er es eigentlich müsste. Um seine Argumentation zu stützen, stellt Eschenbach eine Energiebilanz unserer Erde nach Kiehl & Trenberth vor. Entgegen dem Original von K&T sei das von ihm vorgestellte Modell in Abbildung 2 aber für alle atmosphärischen Schichten und die Erdoberfläche energetisch ausbalanciert, Zitat:
“…this one is balanced, with the same amount of energy entering and leaving the surface and each of the atmospheric layers.”
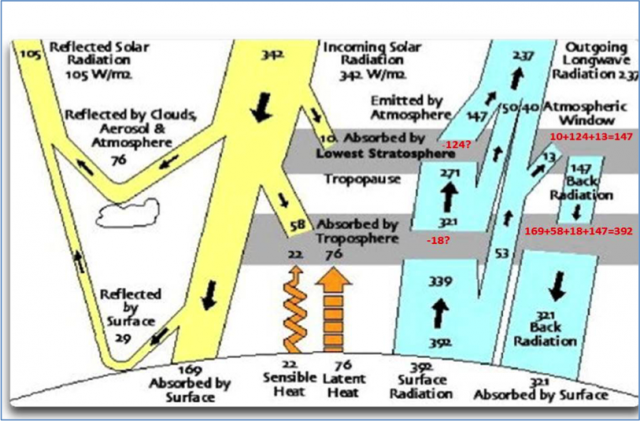
Abbildung 2: Globales Energiebudget nach Kiehl&Trenberth aus Eschenbach @ WUWT
(die roten Zahlen wurden vom Autor zusätzlich eingefügt)
Die Zahlenangaben auf der linken Seite des Diagramms sind verständlich und nachvollziehbar, während die rechte Seite trotz der vom Autor in rot ergänzten Zahlenwerte auch weiterhin kryptisch bleibt. An dieser Stelle sei darauf hingewiesen, dass die übliche globale Energiebilanz nach Kiehl & Trenberth nichts mit der tatsächlichen Temperaturgenese unserer Erde zu tun hat, auch wenn sie im konventionellen S-B Ansatz zur Ermittlung einer theoretischen Durchschnittstemperatur immer wieder gerne verwendet wird, wie Abbildung 3 verdeutlicht.
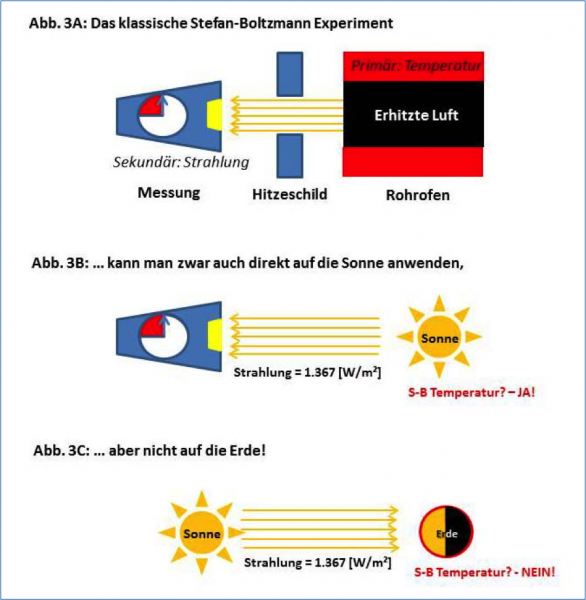
Abbildung 3: Die praktische Anwendung des Stefan-Boltzmann-Gesetzes
In Abbildung 3A sieht man das klassische Stefan-Boltzmann-Experiment. Mit dessen Umkehrung kann man beispielsweise unmittelbar die Temperatur der Sonne bestimmen, wie Abbildung 3B zeigt. Das S-B Gesetz beschreibt also das Verhältnis zwischen der Temperatur eines erhitzten Körpers und seiner originären Strahlung im thermischen Gleichgewicht, das im S-B Gesetz durch das Gleichheitszeichen dargestellt wird. Und in Abbildung 3C sehen wir dann einen kalten Körper, der passiv von der Sonne bestrahlt wird. Egal wie man sich auch dreht und wendet, bei einem T4-Gesetz kann man der Sonneneinstrahlung nicht willkürlich eine beliebige bestrahlte Fläche auf der Erde zuschreiben, für die dann „freihändig“ eine Gleichgewichtstemperatur mit dem S-B Gesetz berechnet wird, sondern muss sich auf die direkt bestrahlte Hemisphäre beschränken. Und daher kann man aus einer durchschnittlichen Energiebilanz für die ganze Erde auch keine durchschnittliche Globaltemperatur ableiten, denn damit würde man das Stefan-Boltzmann-Gesetz als profane Rechenanweisung missbrauchen. Für unsere Erde als passiv beleuchteten Körper hat das Stefan-Boltzmann-Gesetz also nur eine recht begrenzte Aussagefähigkeit, nämlich:
Wenn die Erde eine Temperatur von -19 Grad Celsius hätte, würde sie nach dem Stefan-Boltzmann-Gesetz über ihre gesamte Oberfläche mit 235 W/m² abstrahlen.
Diese Aussage beweist aber nicht, dass die Erde tatsächlich eine solche Temperatur besitzt. Schon gar nicht kann man aber die solare Einstrahlung vierteln und damit über die gesamte Erdoberfläche verteilen, wie das auch Eschenbach in seinem Artikel macht. Diese Kritik führt uns dann direkt zu meinem hemisphärischen Stefan-Boltzmann Ansatz, nach dem die gemessene Durchschnittstemperatur unserer Erde von 14,8 °C durch den Wärmeinhalt der globalen Zirkulationen bestimmt wird. Dazu gerne ein anderes Mal mehr und jetzt zurück zu Eschenbach. Die zentrale Aussage seines Artikels ist, eine kalte Atmosphäre könne die Erde vor etwas noch kälterem schützen, nämlich vor dem Weltall, Zitat:
„BUT a cold atmosphere can leave the earth warmer than it would be without the atmosphere because it is hiding something even colder from view, the cosmic microwave background radiation that is only a paltry 3 W/m2. And as a result, with the cold atmosphere shielding us from the nearly infinite heat sink of outer space, the earth ends up much warmer than it would be without the cold atmosphere.”
Diese Sichtweise von Eschenbach hat aber keinerlei physikalische Relevanz. Kälte ist nämlich nicht etwa als „negative Strahlung“ eine eigenständige physikalische Größe, sondern beschreibt umgangssprachlich lediglich die Abwesenheit von gefühlter Wärme. Die Physik bezeichnet dagegen jede Temperatur über dem absoluten Nullpunkt von 0 °K als „Wärme“. Eine solche Argumentation wie die von Eschenbachs geht also völlig an der physikalischen Realität vorbei und damit fällt auch der Ansatz, man könne einen warmen Körper aktiv vor einer auf ihn eindringenden Kälte schützen.
Vielmehr gibt es genau für diesen Fall die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes, die in Abbildung 4 dargestellt ist.
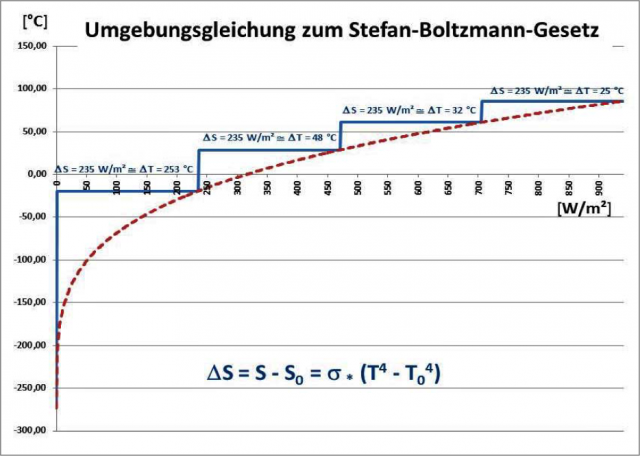
Abbildung 4: Die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes
Rot gestrichelt: Die T4-Beziehung des S-B Gesetzes zwischen Strahlung und Temperatur
Blaue Treppenfunktion: Das unterschiedliche Temperaturäquivalent für jeweils 235 W/m²
Nach der S-B Umgebungsgleichung ergibt sich bei einem beliebigen Abstrahlungswert in [W/m²] keine eindeutige Lösung für den betreffenden Temperaturbereich, in dem diese Abstrahlung stattfindet. Für eine solche eindeutige Lösung ist vielmehr die Kenntnis der S-B Umgebungstemperatur T0 zwingend erforderlich.
Der Knackpunkt von Eschenbachs Modell ist also die S-B Umgebungstemperatur T0, die eben nicht von der Temperatur des Weltraums oder einer ominösen atmosphärischen Gegenstrahlung vorgegeben wird, sondern allein vom Wärmeinhalt der globalen Zirkulationen.