Machen wir mal ein Gedankenexperiment: Es gibt gar keine Erde!
- Die Erde hat zwar ein heißes Inneres, aber der Wärmestrom an ihrer Oberfläche ist äußerst gering. Auch die Gezeitenreibung liefert keine klimawirksame Energie. Die alleinige „natürliche“ Eigentemperatur der Erde würde vielmehr bei etwa minus 240 Grad Celsius liegen. Die Erde selbst ist also primär an der Temperaturgenese auf ihrer Oberfläche nicht beteiligt.
- Die Sonne ist der bestimmende Energielieferant für die Temperatur- und Klimagenese auf unserer Erde; die Sonne ist also ihr eigentlicher Klimamotor.
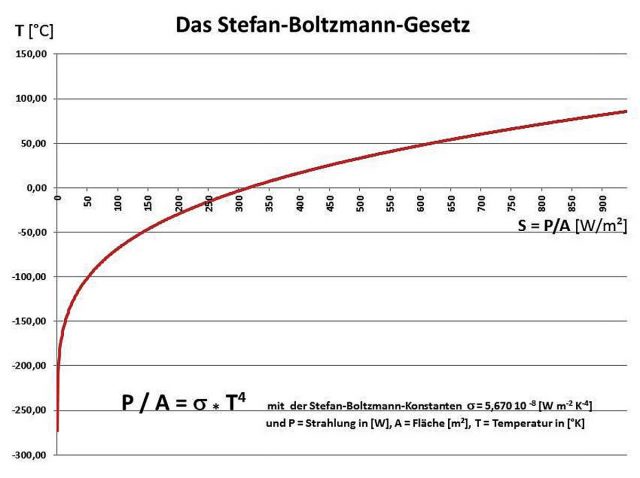
- Und das Stefan-Boltzmann-Gesetz beschreibt den physikalischen Zusammenhang von Strahlung und Temperatur.
Das Stefan-Boltzmann-Gesetz kann also, bei richtiger Anwendung, zur Beschreibung der Temperatur- und Klimagenese unserer Erde dienen. Es beschreibt für einen Schwarzen Körper den in Abbildung 1 dargestellten physikalischen Zusammenhang von Strahlung und Temperatur im thermischen Gleichgewicht:
Das Gleichheitszeichen im Stefan-Boltzmann-Gesetz bedeutet aber leider nicht, dass man einfach irgendwelche Durchschnittswerte in dieses physikalische Gesetz einsetzen darf, um die Situation auf der Erde zu beschreiben, denn dieses S-B Gesetz ist eben ein Gesetz und keine Gleichung. Es stellt vielmehr einen direkten physikalischen Bezug von singulären Strahlungs- und Temperaturwerten im gemeinsamen thermischen Gleichgewicht her. Und nur in diesem Gleichgewichtszustand entspricht ein konkreter Strahlungswert einer durch dieses Gesetz eindeutig definierten Temperatur nach der in Abbildung 1 dargestellten Funktion. Die jeweilige Temperatur muss also physikalisch konkret vorliegen, um den spezifischen Strahlungswert nach dem Stefan-Boltzmann-Gesetz zu erzeugen.
1. ERKENNTNIS: Berechnungen von und aus Durchschnittswerten sind mit dem Stefan-Boltzmann-Gesetz physikalisch nicht zulässig. Eine Berechnung von Mittelwerten kann vielmehr erst dann durchgeführt werden, wenn bereits für alle beteiligten Wertepaare von Temperatur und Strahlung eine individuelle Umrechnung nach dem Stefan-Boltzmann-Gesetz erfolgt ist. Grundvoraussetzung ist, dass diese Wertepaare in einer direkten physikalischen Beziehung miteinander stehen müssen.
Machen wir an dieser Stelle zunächst einmal ein Gedankenexperiment: Es gibt gar keine Erde!
Dazu verbringen wir zu einem Zeitpunkt “0” ein Duplikat unserer Erde aus einem Dunkelkammer-Weltraumlabor an den aktuellen Standort unserer Erde. Dieses Duplikat soll eine voll funktionsfähige Erde in einem „tiefgefrorenen“ Zustand mit einer Eigentemperatur von minus 240 Grad Celsius darstellen:
- Nun setzen wir dieses Duplikat unserer Erde zum Zeitpunkt „0“ der Sonnenstrahlung aus und messen die Zeit „A“, bis die aktuelle Temperaturverteilung auf unserer Erde erreicht ist und alle atmosphärischen und ozeanischen Zirkulationen mit Wärmeenergie „aufgeladen“ sind. Dieser Zeitpunkt „A“ ist gekennzeichnet durch ein erstmaliges Gleichgewicht von eingestrahlter und abgestrahlter Energiemenge.
- Nachdem dieser Gleichgewichtszustand erreicht wurde, verbringen wir das Duplikat unserer Erde zum Zeitpunkt „B“ wieder ins Labor und messen den Zeitraum „b”, bis wieder die ursprüngliche Ausgangstemperatur von etwa 240 Grad Celsius herrscht.
Wir werden dann herausfinden, dass beide Zeiten “A” und “b” größer als “Null” sind. Die Zeit “A” repräsentiert ein Maß für die Wärmekapazität unserer Erde, während die Zeit “b” ein Maß für die Qualität der thermischen Isolierung unserer Erde gegen das Weltall darstellt. „A“ und „b” repräsentieren in erster Näherung einen Zeitraum von Jahrhunderten bis Jahrtausenden. Das Stefan-Boltzmann-Gesetz gilt aber nur in einem thermischen Gleichgewichtszustand zwischen Strahlung und Temperatur, also im Zeitraum „t“ mit (A < t < B). In einem solchen Gleichgewichtszustand spielt aber die Wärmekapazität zunächst keine Rolle. Die einzige temperaturbestimmende Einflussgröße im thermischen Gleichgewichtszustand auf unserer Erde ist damit die eingestrahlte Energie von der Sonne in [W/m²] auf der Tagseite. Wie groß der Energieinhalt des Systems Erde dabei wirklich ist und wie lange die Aufladung gedauert hat, ist dafür zunächst unerheblich, wenn wir diesen Zeitraum „t“ mit (A < t < B) betrachten.
Dieser statische Fall zeichnet sich offensichtlich durch eine relativ stabile globale Durchschnittstemperatur (NST=Near Surface Temperature) von 14,8 Grad Celsius aus. Die globalen Zirkulationen sind mit Energie „gesättigt“ und alle atmosphärischen und ozeanischen Prozesse sind in eine Art mittleren klimatischen Gleichgewichtszustand „eingeschwungen“ – das Wettergeschehen spiele in dieser Abstraktion keine Rolle. Bei einer solchen statischen Betrachtung ergeben sich dann folgende Rechengrößen:
Solarkonstante: 1.367 W/m²
Temperaturwirksame Sonneneinstrahlung: 940 W/m²
Durchschnittliche Abstrahlung nach Energiebilanz: 235 W/m²
Anmerkung: Um den Beweisweg nicht zu komplizieren, werden hier vereinfachte Werte zugrunde gelegt. Der hemisphärische Zweischichtfall für Atmosphäre und Oberfläche mit einer temperaturwirksamen Nettostrahlung von 780 W/m² wird hier nicht betrachtet.
Für eine hemisphärische Sonneneinstrahlung von 940 W/m² bei lotrechter Position der Sonne ergibt sich nach dem Stefan-Boltzmann-Gesetz dann eine maximale Gleichgewichtstemperatur von 85,7 Grad Celsius. Und eine beliebige örtliche SB-Maximaltemperatur lässt sich in Abhängigkeit von der geographischen Breite mit dem hemisphärischen S-B Ansatz folgendermaßen beschreiben:
S,Z = 940 [W/m²] * cos mit S,,Z = breitenabhängiger hemisphärischer Netto-Strahlungsantrieb im solaren Zenit und =auf den jahreszeitlichen Sonnenstand korrigierte Breite der Ortslage
Die aus dieser S-B Beziehung ableitbaren hemisphärischen S-B Gleichgewichtstemperaturen werden auf der Erde weder im Maximum noch im Minimum erreicht. Wenden wir uns daher zunächst einmal dem Mond als vergleichbarem Himmelskörper ohne Ozeane und Atmosphäre zu. Nachfolgend ist eine Abbildung dargestellt, die bereits auf EIKE veröffentlicht worden war:
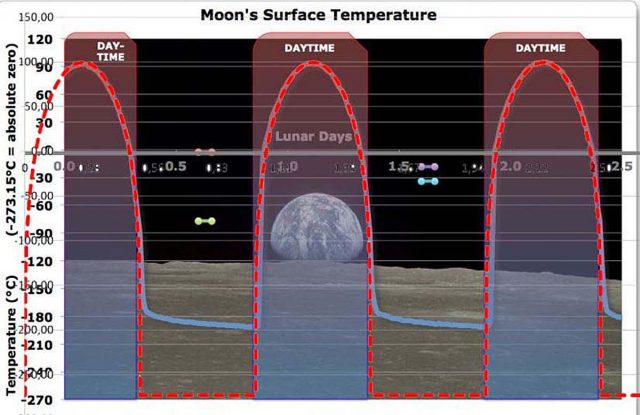
Abbildung 2: Vergleich der gemessenen Oberflächentemperatur auf dem Mond (blau) mit der hemisphärischen S-B Gleichgewichtstemperatur (rot)
Blau: Gemessene Oberflächentemperatur auf dem Mond am Landeplatz von Apollo 15
Zugrunde liegt die Originalabbildung aus einem EIKE-Artikel (Primärquelle Eschenbach auf WUWT)
Rot: Verlauf der hemisphärischen S-B Gleichgewichtstemperatur für die geographischen Position des Apollo 15 Landeplatzes ohne Berücksichtigung der lunaren Achsenneigung mit den nachfolgenden Eckwerten:
Landepunkt von Apollo 15: Mond @ 26° 7′ 55.99″ N 3° 38′ 1.9″ E
Solarkonstante: 1.367 [W/m²]
Albedo des Mondes: 0,11
Temperaturwirksame Solarstrahlung: 1.217 [W/m²]
dito bei 26,125° geogr. Breite: 1.092 [W/m²]
Effektive Solarstrahlung Seff für α = [0° – 360°]: IF SIN α >0 THEN Seff = SIN α* 1.092 [W/m²]
IF SIN α <0 THEN Seff = 0 [W/m²]
Abbildung 2 zeigt, dass die gemessene und die hemisphärisch berechnete S-B Gleichgewichtstemperatur am Landepunkt von Apollo 15 bei Tage hervorragend überein stimmen, während die Nacht-Temperaturen um etwa 70 Grad differieren. Diese Differenz ist aber eher ein Problem zwischen Theorie und Praxis, denn in der S-B Berechnung wird für die Nachtseite des Mondes streng mit 0 [W/m²] gerechnet, während der Mond in der Realität reflektierte Sonnenstrahlung von der Erde erhält, deren Albedo immerhin etwa 30% betragt. Eine Temperatur von -196 °C entspricht nach Stefan-Boltzmann einer Strahlung von 2 {W/m²], wie Abbildung 1 erkennen lässt, und dafür dürfte die Rückstrahlung der Erde von etwa 400 [W/m²] allemal ausreichen.
2. ERKENNTNIS: Auf dem Mond funktioniert der hemisphärische S-B Ansatz ganz hervorragend, warum sollte er also für die Erde nicht anwendbar sein?
Im konventionellen S-B Ansatz wird eine globale Durchschnittstemperatur aus der durchschnittlichen Energiebilanz der Erde mit einem Viertel der wirksamen Solarkonstanten ermittelt. Wie wir bereits gesehen haben, „verkraftet“ das Stefan-Boltzmann-Gesetz solche Durchschnittswerte aber gar nicht.
Schauen wir aber trotzdem einmal näher hin und beschränken wir uns auf die Abstrahlung:
Die durchschnittliche globale Abstrahlung unserer Erde kann in erster Näherung unter Berücksichtigung der Albedo tatsächlich mit einem Viertel der temperaturwirksamen netto-Sonneneinstrahlung von 235 W/m² beschrieben werden, auch wenn sie in Wahrheit sicherlich tages- und jahreszeitlichen sowie breitenabhängigen Schwankungen unterworfen ist.
Nur zur Erinnerung: Diese Betrachtung der Erde findet im Zeitraum „t“ mit (A < t < B) statt.
Die Wärmespeicher des Systems Erde sind also „voll aufgeladen“ und die globale Abstrahlung geschieht kontinuierlich parallel zur hemisphärisch getakteten solaren Einstrahlung. Beim Mond war das ja noch ganz einfach, denn der verfügt neben seiner Oberfläche über keine zusätzlichen Wärmespeicher. Damit stellt sich die Frage, wo bei einer Betrachtung nach der globalen Strahlungsbilanz eigentlich der Wärmeinhalt der globalen Zirkulationen berücksichtigt wird.
3. ERKENNTNIS: Im Gegensatz zum Mond kühlt unsere Erde über Nacht nicht schnell genug aus.
Das Stefan-Boltzmann-Gesetz für einen schwarzen Körper in einer erwärmten Umgebung lautet nun:
S = S – S0 = * (T4 – T04) mit S = P/A [W/m²] Quelle: Gerthsen-Kneser “Physik” (1971)
Nach Abbildung 3 ist es also nach dem Stefan-Boltzmann-Gesetz überhaupt nicht egal, bei welcher Umgebungstemperatur „T0“ wir eine globale Emission von S=235 W/m² ansetzen:
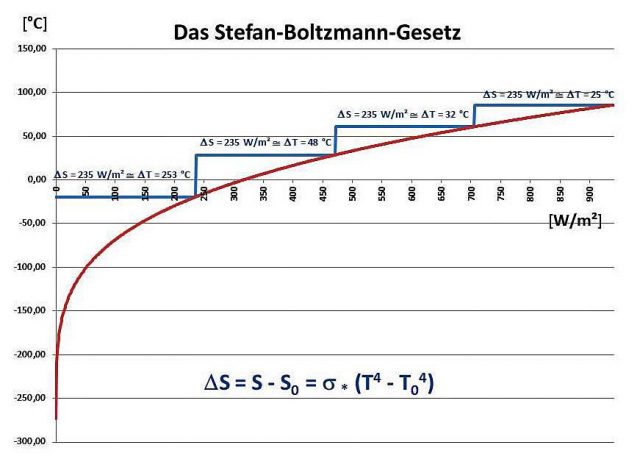
Abbildung 3: Der Temperaturbereich für eine pauschale Abstrahlung von S = 235 W/m² ist abhängig von der Basistemperatur T0 und ergibt nach dem S-B Gesetz keine eindeutige Lösung
Rot: Der Zusammenhang von Strahlung und Temperatur nach dem Stefan-Boltzmann-Gesetz aus Abbildung 1
Blau: Das S-B Temperaturäquivalent für S = 235 W/m² abhängig von der jeweiligen Umgebungstemperatur T0
Abbildung 3 macht also deutlich, dass es beim Stefan-Boltzmann-Gesetz von ganz entscheidender Bedeutung ist, bei welcher Umgebungstemperatur eine Abstrahlung nach der globalen Energiebilanz erfolgt. Jedenfalls kann die Temperatur eines Schwarzen Körpers nicht unter seine Umgebungstemperatur fallen.
4. ERKENNTNIS: Mit der Umgebungsgleichung des S-B Gesetzes ist jetzt das einzige Manko der hemisphärischen S-B Ableitung geheilt, nämlich das Fehlen einer Erklärung für das Verhalten der örtlichen Nachttemperatur.
Der konventionelle S-B Ansatz aus der globalen Energiebilanz geht nun davon aus, dass das Umgebungsniveau „T0“ unserer Erde null Grad Kelvin beträgt. Von dort aus werden nämlich nach S-B die ominösen 18 Grad Celsius mit S = 235 W/m² „hochgerechnet“, wie das in Abbildung 3 durch die erste „Treppenstufe“ von 0 bis 235 W/m² dargestellt wird. Die konventionelle S-B Ableitung für die „natürliche“ globale Durchschnittstemperatur von 18 °C ignoriert also den Wärmeinhalt der globalen Zirkulationen als unmittelbar wirksame Wärmespeicher unserer Erde.
5. ERKENNTNIS: Allein der Wärmeinhalt der globalen Zirkulationen sorgt dafür, dass das Temperaturniveau der Erde nachts nicht in die Nähe von null Grad Kelvin zurückfällt, wie wir das auf dem Mond beobachten können.
Abschätzung für die S-B Größe „T0“ in dieser Betrachtung: Das „T0“ in der S-B Umgebungsgleichung dürfte in etwa durch die global gemittelte Morgentemperatur der Ozeane kurz vor Sonnenaufgang repräsentiert werden. In dem auf EIKE veröffentlichten Artikel „Über die schwer fassbare globale mittlere Temperatur – ein Vergleich Modell ? Daten “ (von Bob Tisdale, übersetzt von Chris Frey, EIKE) heißt es über die durchschnittlichen Meerestemperaturen, Zitat:
„Die mittlere absolute globale Wassertemperatur ICOADS beträgt während der letzten 30 Jahre (1984 bis 2013) 19,5°C, während deren absolute globale Wassertemperatur 19,3°C beträgt.“
Zunächst einmal ist hier festzustellen, dass die globalen Durchschnittswerte der oberflächennahen Bodentemperatur (NST) und der Wassertemperatur stark differieren. Diese Differenz dürfte aber eher der natürlichen Begrenzung der Wassertemperatur durch den Gefrierpunkt des Wassers geschuldet sein. An diesem begrenzten Minusbereich für die Wassertemperatur scheitert also eine direkte Vergleichbarkeit beider Durchschnittswerte. Setzen wir hier also einfach einmal voraus, dass sich beide Durchschnittstemperaturen (Land und Meer) in etwa entsprechen würden. Da aber die globale Wassertemperatur zu tiefen Temperaturen hin eingeschränkt ist liegt es nahe, als gemeinsame Basis auf die durchschnittliche oberflächennahe Lufttemperatur zurückzugreifen. Und wenn wir in der S-B Umgebungsgleichung als Ausgangswert „T0“ diese global gemittelte gemessene Durchschnittstemperatur (NST) von 14,8 Grad Celsius ansetzen, dann ist der imaginäre atmosphärische Treibhauseffekt plötzlich verschwunden.
6. ERKENNTNIS: Wenn die bodennahe örtliche Nachttemperatur nach der Umgebungsgleichung des S-B Gesetzes durch einen Wärmezufluss aus den atmosphärischen und ozeanischen Zirkulationen gestützt wird, dann sind alle weiteren Spekulationen über einen „natürlichen“ atmosphärischen Treibhauseffekt hinfällig.
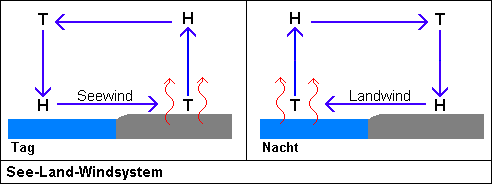
Sinkt also nachts die örtliche bodennahe Temperatur unter die Temperatur des ortsnahen Ozeans, dann erfolgt sofort ein Wärmefluss aus diesem Wärmespeicher. Anstelle einer weiteren Abkühlung der betrachteten Senke erfolgt dann also ein zusätzlicher Wärmefluss in diese Senke hinein. Im Umkehrschluss wird diese Senke also umso tiefer werden, je weiter entfernt vom Ozean sie sich befindet. Für eine anschauliche Darstellung des tageszyklischen Wärmeaustausches von Land und Meer wird hier auf Wikipedia verwiesen.
Anmerkung: Der direkte Einfluss der Atmosphäre wird hier nicht weiter diskutiert, weil sie sehr viel komplizierter zu beschreiben ist. Der Wärmeinhalt der Atmosphäre selbst weist nämlich wegen stark schwankender Wassergehalte eine wesentlich größere Variabilität auf und eine Wolkenbedeckung kann außerdem die nächtliche Abstrahlung deutlich vermindern.
Wenn wir jetzt einmal realistisch das S-B Temperaturäquivalent für eine globale Abstrahlung von S = 235 W/m² betrachten, dann dürften wir irgendwo im Bereich der zweiten „Treppenstufe“ in Abbildung 3 fündig werden, also im Bereich von T = 48 Grad Celsius. Dieser Wert ist als tägliche Schwankungsbreite selbst für extreme Wüstengebiete sehr ambitioniert, also dort, wo die globalen Zirkulationen nur einen geringen Beitrag gegen die Nachtabkühlung liefern können. Für die meisten individuellen Ortslagen kommt also im Umkehrschluss tatsächlich ein unterstützender Wärmestrom aus den globalen Zirkulationen zum Tragen. Das in Abbildung 4 dargestellte Jahresmittel des Energiehaushaltes der Atmosphäre und seiner Komponenten in Abhängigkeit von der geographischen Breite nach HÄCKEL (1990) weist diesen Zusammenhang eindeutig nach.
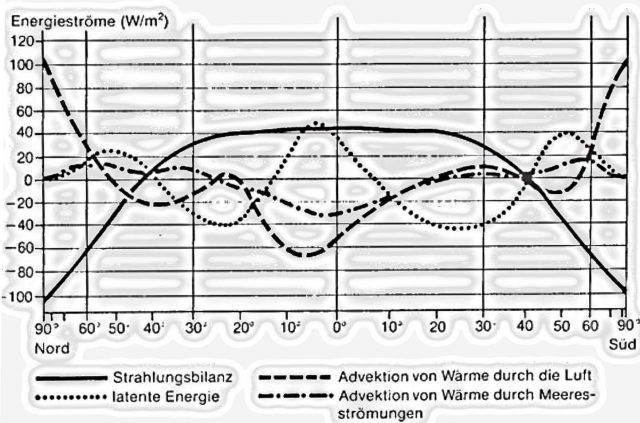
Abbildung 4: Jahresmittel des Energiehaushaltes der Atmosphäre und seiner Komponenten in Abhängigkeit von der geographischen Breite. QUELLE: HÄCKEL, Meteorologie, Verlag Eugen Ulmer, Stuttgart 1990, zu finden auch hier
Diese Abbildung 4 zeigt zum Beweis der oben gemachten Ausführungen den durchschnittlichen horizontal verfrachteten jährlichen Wärmestrom durch die globalen Zirkulationen in mittlere und höhere geographische Breiten hinein. Da die abschließende Argumentation über die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes auf der globalen Energiebilanz von 235 W/m² aufsetzt, reiht sich diese Abbildung 4 von Häckel (1990), die ebenfalls auf einer Energiebilanz von 235 W/m² beruht, widerspruchslos in die vorliegende Argumentation ein und weist deren Richtigkeit nach.
7. ERKENNTNIS: Die theoretische Schwankungsbreite für das Temperaturäquivalent einer durchschnittlichen globalen Abstrahlung von 235 W/m² kann, außer vielleicht in extremen Wüstengebieten, auf der Erde kaum erreicht werden. Vielmehr wirkt der Wärmezufluss aus Atmosphäre und Ozeanen einer örtlichen Nachtabsenkung der Temperaturen entgegen.
Fassen wir die Temperaturgenese auf unserer Erde also noch einmal abschließend zusammen:
- Die Sonne heizt auf der Tagseite der Erde Landflächen, Atmosphäre und Ozeane auf.
- Die hemisphärisch berechnete Maximaltemperatur nach dem Stefan-Boltzmann-Gesetz wird dabei nirgendwo auf der Erde erreicht. Vielmehr werden insbesondere in niederen und mittleren Breiten die globalen Zirkulationen tagsüber mit Wärmeenergie „aufgeladen“.
- Der Wärmeinhalt in den globalen Zirkulationen wird also auf der Tagseite aus der hemisphärischen Sonneneinstrahlung gespeist, was dort zu einer Reduzierung der gemessenen Temperaturen gegenüber den berechneten hemisphärischen S-B Gleichgewichtstemperaturen führt.
- Für eine individuell betrachtete Ortslage auf der Nachtseite der Erde bestimmen der Wassergehalt der Atmosphäre und die Entfernung zum Ozean, wie stark sich die Erdoberfläche dort abkühlen kann.
- Damit ist die Nachtabkühlung in meeresnahen äquatorialen Gebieten am geringsten und in kontinentalen Wüstengebieten niederer Breiten am größten.
- Der Wärmezufluss aus den globalen Zirkulationen trägt also zur örtlich gemessenen Nachttemperatur bei. Diese Wärmeflüsse sorgen während des jeweiligen Winterhalbjahres in mittleren und höheren geographischen Breiten auch für einen generellen Temperaturanstieg gegenüber den hemisphärisch berechneten S-B Gleichgewichtstemperaturen.
Am Ende führen also eine physikalisch falsche Anwendung des Stefan-Boltzmann-Gesetzes und die Nichtbeachtung des Wärmeinhalts der globalen Zirkulationen bei der konventionellen S-B Herleitung einer globalen Durchschnittstemperatur über die Energiebilanz unserer Erde zu einem imaginären „natürlichen atmosphärischen Treibhauseffekt“ von 33 Grad. Tatsächlich aber folgt die globale Temperaturgenese auf der Erde einem hemisphärischen Strahlungsansatz über das Stefan-Boltzmann-Gesetz, während die Nachtabkühlung auf der Erde mit der Umgebungsgleichung des Stefan-Boltzmann-Gesetzes unter Einbeziehung des Wärmeinhaltes der globalen Zirkulationen beschrieben werden kann.
ERGEBNIS: Es sind in Wirklichkeit also die wärmebeladenen globalen Zirkulationen, die unter dem Pseudonym „natürlicher atmosphärischer Treibhauseffekt“ für lebensfreundliche Temperaturen auf unserer Erde sorgen, indem sie hier auf der Erde eine dem Mond vergleichbare extreme Schwankung von tageszyklischer Aufheizung und Nachtabsenkung verhindern.
Schlussbemerkung: Wegen des imaginären Konstruktes eines „natürlichen atmosphärischen Treibhauseffektes“ aus einer fehlerhaften Anwendung des Stefan-Boltzmann-Gesetzes sollen wir uns jetzt also alle einer „globalen Dekarbonisierung bis zum Jahre 2100“ unterziehen. Und damit wird dann unsere fossil betriebene Industrie, unser damit erwirtschafteter Lebensstandard sowie auch noch die Überlebensperspektive zukünftiger Generationen zerstört – ja geht’s denn eigentlich noch?