Beweist die Temperatur des Mondes den hemisphärischen Stefan-Boltzmann Ansatz?
Uli Weber
Die Fragen in meinem Artikel auf EIKE, „Noch ein paar Fragen zum „natürlichen“ atmosphärischen Treibhauseffekt“, wurden zwar nicht beantwortet, aber dafür wurde der Artikel wieder einmal sehr kontrovers diskutiert. Ich nehme den dankenswerten Vorschlag eines Kommentators daher diesmal gerne auf, um ihn einmal über die tatsächlichen physikalischen Grundlagen aufzuklären. Denn eine solche Darstellung grundlegender physikalischer Zusammenhänge könnte schließlich auch noch weiteren Kommentatoren aufs Pferd helfen.
Also schaunmerdiesmal bitte ganz konzentriert hin:
Das Stefan-Boltzmann-Gesetz ist keine simple Rechenanleitung, sondern ein physikalisches Gesetz. Und das dort enthaltene Gleichheitszeichen ist kein mathematisches Gleichheitszeichen, sondern eine zwingende physikalische Bedingung.
Man kann dieses Gesetz also nicht einfach als mathematische Formel missbrauchen, um beliebige Durchschnittstemperaturen in irgendeine Strahlungsleistung umzurechnen oder umgekehrt. Vielmehr ist nach diesem Gesetz eine ganz konkrete Temperatur ganz ausschließlich einem bestimmten Strahlungswert zugeordnet. Und das Gleichheitszeichen zwischen Strahlung und Temperatur steht als zwingende Bedingung dieses Gesetzes für ein gemeinsames thermisches Gleichgewicht genau zwischen diesen beiden physikalischen Größen.
Das bedeutet, das Gleichheitszeichen im Stefan-Boltzmann-Gesetz bezieht sich auf einen gleichzeitigen Zusammenhang zwischen Strahlung und Temperatur, nämlich Temperatur erzeugt Strahlung oder Strahlung erzeugt Temperatur, und zwar jetzt, hier, in diesem Augenblick – und nicht erst später auf der Nachtseite der Erde. Und genau deshalb heißt dieser physikalische Zusammenhang ja auch Stefan-Boltzmann-Gesetz und nicht etwa Stefan-Boltzmann-Gleichung.
Die geometrischen Verhältnisse für die Sonneneinstrahlung auf unserer Erde sind eigentlich ganz einfach zu verstehen (beide nachfolgenden Abbildungen aus meinem neuen Buch „Klima-Mord“):

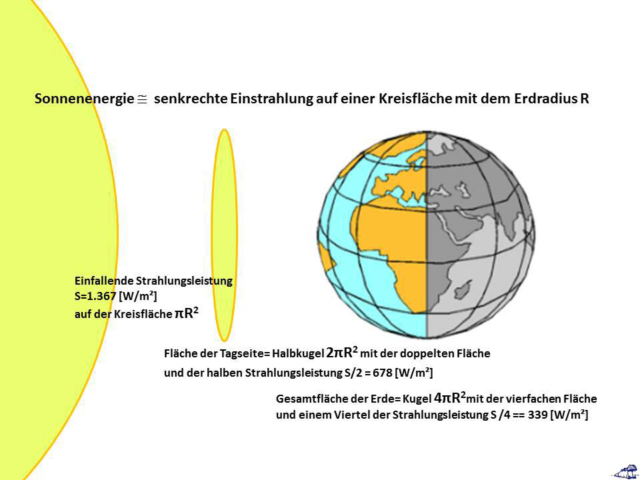
Das Sonnenlicht trifft praktisch als ebene Wellenfront auf die Atmosphäre unserer Erde. Daraus ergeben sich dann die nachfolgend dargestellten geometrischen Verhältnisse:
- Die Strahlung der Sonne trifft mit einer Kreisfläche von (pR²) auf die Erde,
- Diese Strahlung verteilt sich auf der Tagseite der Erde, also auf einer Halbkugel mit (2pR²)
- Die Gesamtfläche der Erde ist eine Kugeloberfläche mit (4pR²)
Die beteiligen Flächen haben also das Verhältnis von 1 : 2 : 4.
Wie wir in der Erklärung des Stefan-Boltzmann-Gesetzes gesehen haben, kann man nach diesem Gesetz nur diejenigen Größen ins Verhältnis setzen, die direkt in einem gleichzeitigen thermischen Verhältnis miteinander stehen. Gleichzeitig beteiligt an der Temperaturgenese auf unserer Erde sind aber ausschließlich die einfallende Sonnenstrahlung mit (pR²) und die Tagseite der Erde mit (2pR²). Für die ursprüngliche Sonneneinstrahlung von 1.367 [W/m²] ergibt sich daher der Divisor 2 für den Strahlungsdurchschnitt auf der Tagseite der Erde.
Hier auf der Tagseite der Erde, und nur hier, gilt das Stefan-Boltzmann-Gesetz. Die Nachtseite der Erde hat mit der S-B Gleichgewichtstemperatur auf der Tagseite überhaupt nichts zu tun, weil sie ja keine temperaturgenerierende Sonnenstrahlung erhält.
Und jetzt widmen wir uns einmal dem Mond, der ja argumentativ immer wieder gerne als ein Beispiel für einen idealen atmosphärelosen Schwarzkörper herangezogen wird und, im Vergleich zur Erde, auch als Beweis für den „natürlichen“ atmosphärischen Treibhauseffekt herhalten muss. Ich zitiere einen Kommentar zu meinem Artikel auf EIKE:
„Die Apollo 15 Landestelle hat eine ungefähre Durchschnittstemperatur von 252 K, Tmassah, das auf ähnlicher Breite, aber auf der Erde (Sahara) liegt, hat 295 K Durchschnittstemperatur.
Macht einen „Atmosphäreneffekt“ vom 43K. Oder liege ich mit meinem Ansatz falsch?“
Meine Antwort: Ja, Sie machen da etwas grundsätzlich falsch, denn Sie stellen hier einen unzulässigen Vergleich an. Die von Ihnen genannten Durchschnittstemperaturen beziehen nämlich die Nachtseiten von Mond und Erde mit ein. Und die Nachtseite des Mondes hat nun einmal ein ganz anderes Temperaturverhalten als die Nachtseite der Erde. Nach den oben beschriebenen Randbedingungen des Stefan-Boltzmann-Gesetzes kann man nämlich nur die entsprechenden Tagestemperaturen miteinander vergleichen.
Aberschaunmereinfachmalgenauernach: In einem älteren Artikel auf EIKE wurden die am Landeplatz von Apollo 15 gemessenen Mondtemperaturen in einer Grafiküber drei Mond-Tage (= 3 x 29,5 Erdtage) dargestellt:
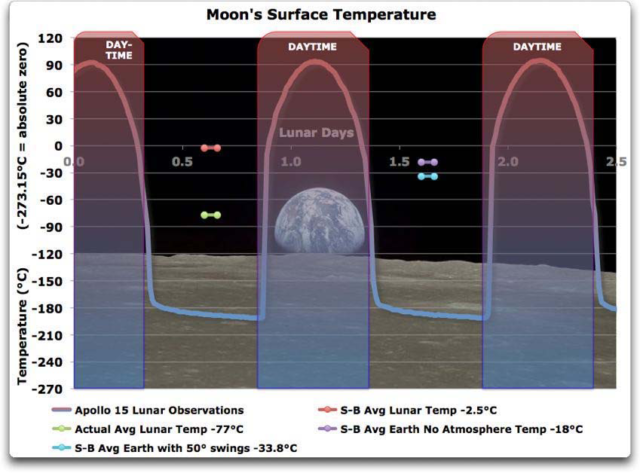
Abbildung: Oberflächentemperatur auf dem Mond am Landeplatz von Apollo 15 (lila/blau)
Aus einem Artikel auf EIKE, Primärquelle WUWT
Nach dieser Abbildung schwanken die Temperaturen über den Mond-Tag (=29,5 Erdtage) an der Landestelle von Apollo 15 zwischen etwa +90 °C und – 190 °C.
Wenn man jetzt für die Landeposition von Apollo 15 einmal die Stefan-Boltzmann Gleichgewichtstemperatur berechnet, dann erhält man einen ziemlich ähnlichen Temperaturverlauf wie die oben dargestellten Messwerte (Abbildung vom Autor):
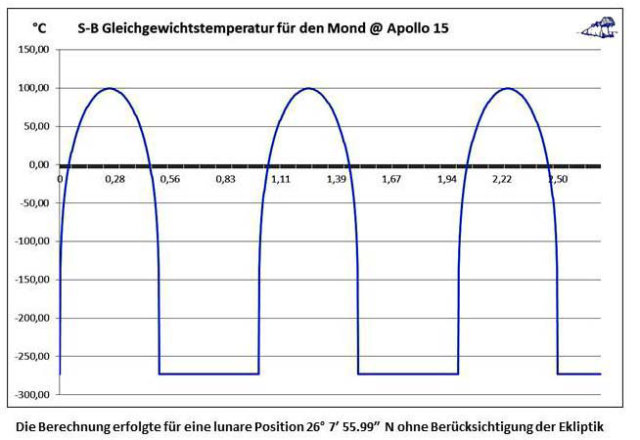
Eckwerte dieser Berechnung:
Landepunkt von Apollo 15: Mond @ 26° 7′ 55.99″ N 3° 38′ 1.9″ E
Solarkonstante: 1.367 [W/m²]
Albedo des Mondes: 0,11
Temperaturwirksame Solarstrahlung: 1.217 [W/m²]
dito bei 26,125° geogr. Breite: 1.092 [W/m²]
Effektive Solarstrahlung Seff für α = [0° – 360°]: IF SIN α >0 THEN Seff = SIN α* 1.092 [W/m²]
IF SIN α <0 THEN Seff = 0 [W/m²]
Und wenn man diese beiden Abbildungen dann übereinander projiziert, ergibt sich eine ganz erstaunliche Übereinstimmung:
Kombination der beiden vorherigen Abbildungen WUWT/Weber:
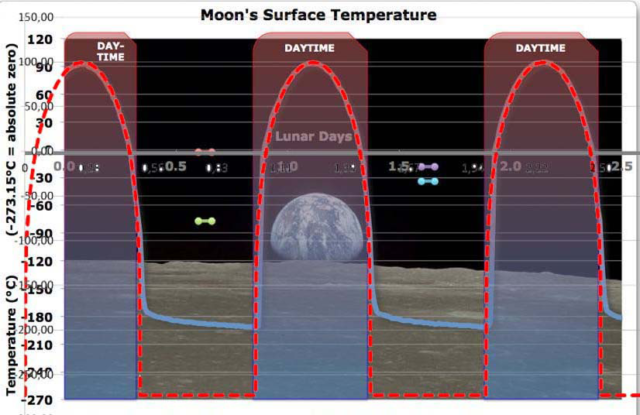
Die gemessene und die mit S-B berechnete Temperatur am Landepunkt von Apollo 15 stimmen bei Tage hervorragend überein, während die minimalen (Nacht-) Temperaturen um etwa 70 bis 90 Grad differieren. Diese Differenz ist aber eher ein Problem zwischen Theorie und Praxis, denn in der S-B Berechnung wird für die Nachtseite des Mondes streng mit 0 [W/m²] gerechnet, während die Nachtseite in der Realität gestreute Sonneneinstrahlung von der Erde erhält, deren Albedo immerhin 30% betragt.
Abschätzung: Eine Temperatur von -196 °C entspricht nach Stefan-Boltzmann einer Strahlung von 2 {W/m²], dafür dürfte die Rückstrahlung der Erde von etwa 418 [W/m²] allemal ausreichen.
Warum schwankt aber nun die Temperatur auf der Erde so viel weniger als auf dem Mond?
Erde und Mond unterscheiden sich zunächst einmal durch ihre Tageslängen von 24 Stunden und 29,5 Erdtagen. Die Erde unterscheidet sich vom Mond weiterhin durch die thermische Speicherfähigkeit ihrer globalen Zirkulationen (Atmosphäre und Ozeane). Die kurze Tageslänge der Erde und ihre Wärmespeicher sorgen also für eine geringe Nachtabkühlung, während die durchschnittliche Nachttemperatur auf dem Mond schnell in den 3-stelligen Minusbereich absinkt.
Der Mond ist daher ein stark vereinfachtes Modell der Erde ohne Atmosphäre und Ozeane.
Was herkömmlich als „natürlicher“ atmosphärischer Treibhauseffekt bezeichnet wird, ist also lediglich der Wärmeinhalt der globalen Zirkulationen auf der Erde. Allein diese Wärmespeicher verhindern eine nächtliche Auskühlung unserer Erde in derselben Größenordnung, wie wir sie beim Mond beobachten können. Während nun aber der Mond ohne Atmosphäre und Ozeane auf seiner Tagseite die S-B Gleichgewichtstemperatur annähernd erreicht, wird auf unserer Erde ein Teil dieser Energie für die thermische Aufladung der globalen Zirkulationen „abgezweigt“. Und wegen dieser Wärmespeicher sinkt die Minimaltemperatur der Erde über Nacht dann wiederum höchstens um einige Dekagrad ab. Wenn man also auf der Erde überhaupt von einem Atmosphäreneffekt sprechen will, dann besteht dieser in einer Dämpfung der örtlichen Temperatur gegen maximale Schwankungen der solar verursachten Temperaturgenese, wie wir sie auf dem Mond beobachten können. Für eine Ortslage in mittlerer geographischer Breite auf der Erde (Potsdam) werden in der nachstehenden Abbildung die im Zeitraum zwischen 1890 und 2013 gemessenen maximalen Monatstemperaturen und die S-B Gleichgewichtstemperatur im Strahlungszenit der Sonne dargestellt:
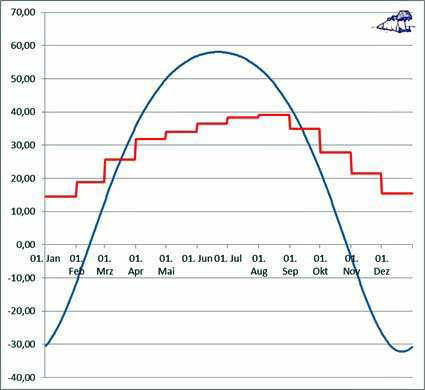
Abbildung: Temperaturvergleich in °C für Potsdam über ein Jahr
Blau: Rechnerische S-B Temperatur im solaren Zenit @Potsdam
Rot: Gemessenes Monatsmaximum in Potsdam im Zeitraum
1890-2013
Anmerkung: Die S-B Gleichgewichtstemperatur im solaren Zenit wurde unter Berücksichtigung der durchschnittlichen globalen Albedo mit netto 780 W/m jahreszeitabhängig berechnet
Daten von: https://www.pik-potsdam.de/services/klima-wetter-potsdam/wetterextreme
Wie diese Abbildung zeigt, bleibt die örtlich gemessene Maximaltemperatur auf der Erde im jeweiligen Sommerhalbjahr deutlich unter der berechneten S-B Gleichgewichtstemperatur. In den Wintermonaten ist in mittleren und höheren Breiten dann der Wärmetransport der globalen Zirkulationen gegenüber der S-B Gleichgewichtstemperatur deutlich zu erkennen, hier noch verstärkt durch die vom Golfstrom verursachte Nordverschiebung der geographischen Klimazonen. Auf der Erde erhöht sich also treibhausmäßig gar nichts, sondern unsere Atmosphäre und die Ozeane wirken vielmehr wie ein natürlicher Pufferspeicher gegen sehr hohe und sehr niedrige Gleichgewichtstemperaturen aus der direkten solaren Einstrahlung.
So, damit ist jetzt hoffentlich endgültig geklärt, dass es gar keinen „natürlichen“ atmosphärischen Treibhauseffekt auf unserer Erde geben kann. Vielmehr lassen sich die gemessenen Temperaturen auf der Erde und auf dem Mond ganz allein aus der natürlichen Sonneneinstrahlung herleiten.
Am Ende habe ich es also meinen schärfsten Kritikern zu danken, dass ich hier, ausgehend von den Temperaturen am Landeplatz von Apollo 15, die Richtigkeit meines hemisphärischen Stefan-Boltzmann Ansatzes mit dem Mond als Kronzeugen nochmals überzeugend nachweisen konnte.
Anmerkung der EIKE Redaktion
EIKE versteht sich auch als Diskussionsforum für Sonder-Hypothesen. Dies bedeutet nicht, dass EIKE mit dem Inhalt solcher Beiträge einverstanden ist. Wir überlassen die Diskussion dem Kommentar-Bereich.