Sind die behaup­teten globalen Rekord-Tempera­turen haltbar?

Ich möchte den geneigten Leser auf das folgende Zitat von Taylor (1982) aufmerksam machen:

Der wichtigste Punkt hinsichtlich der Messungen unserer beiden Experten ist: Wie bei den meisten wissenschaftlichen Messreihen wären beide wertlos gewesen, falls sie nicht zuverlässige Aussagen bzgl. ihrer Unsicherheiten enthalten“.

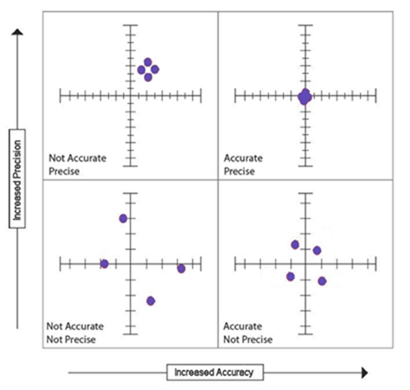
Bevor ich fortfahre ist es wichtig, dass der Leser den Unterschied zwischen Genauigkeit und Präzision versteht. Genauigkeit sagt, wie nahe eine Messung (oder eine Reihe wiederholter Messungen) am tatsächlichen Wert liegt, und Präzision ist die Auflösung, mit der die Messung angegeben werden kann. Eine weitere Möglichkeit zum Verständnis bietet die folgende Graphik:

Die Abbildung impliziert, dass Reproduzierbarkeit oder verringerte Varianz Teil von Präzision ist. Das ist so, aber noch wichtiger ist die Fähigkeit, mit größerer Sicherheit aufzuzeichnen, wo eine Messung im Kontinuum einer Messskala lokalisiert ist. Geringe Genauigkeit ist die Folge systematischer Fehler. Sehr geringe Präzision jedoch, welche sich aus Zufallsfehlern oder ungeeigneter Instrumentierung ergibt, kann dazu beitragen, dass individuelle Messungen geringe Genauigkeit haben.

Genauigkeit

Um die folgende Diskussion nicht zu sehr ausufern zu lassen, werde ich Dinge wie Fehler bei den Örtlichkeiten bei der Aufstellung von Wetterstationen ignorieren, welche potentiell repräsentative Temperaturen korrumpieren und einen Bias einbringen können. Hier kann man sich einen Überblick über diese Probleme verschaffen. Ebenso werde ich die Art und Weise der Datengewinnung ignorieren, welche ein wesentlicher Kritikpunkt bei historischen pH-Messungen war, doch gilt dieses Problem nicht weniger stark auch für Messungen der Temperatur. Grundsätzlich sind Temperaturen räumlich verzerrt mit einer Überrepräsentanz industrialisierter, städtischer Gebiete in den Mittleren Breiten. Und doch werden diese Werte als für den ganzen Globus repräsentativ angegeben.

Es gibt zwei wesentliche Aspekte hinsichtlich der Vertrauenswürdigkeit gegenwärtiger und historischer Temperaturdaten. Ein Aspekt ist die Genauigkeit der aufgezeichneten Temperaturen über die nutzbare Bandbreite der Temperatur, wie sie in Tabelle 4.1 im folgenden Link beschrieben wird:

http://www.nws.noaa.gov/directives/sym/pd01013002curr.pdf

Im Abschnitt 4.1.3 im o. g. Link liest man:

4.1.3 Allgemeine Instrumente. Der WMO zufolge sind gewöhnliche Thermometer in der Lage, mit hoher Genauigkeit Temperaturen in der Bandbreite zwischen -29°C und 46°C zu messen, wobei der maximale Fehler kleiner ist als 0,2°C…

Im Allgemeinen wird von modernen Temperatur-Messgeräten eine Genauigkeit von ±0,56°C bei der Referenztemperatur verlangt sowie ein Fehler, der kleiner ist als ±1,1°C über den Messbereich. Tabelle 4.2 verlangt, dass die Auflösung (Präzision) 0,06°C beträgt mit einer Genauigkeit von 0,2°C.

In den USA gibt es eines der besten Wetterüberwachungssysteme der Welt. Allerdings sollten Genauigkeit und Präzision in dem Zusammenhang betrachtet werden, wie globale Mittelwerte und historische Temperaturen aus den Aufzeichnungen berechnet werden, im besonderen aus jenen mit geringerer Genauigkeit und Präzision. Es ist extrem schwierig, die Genauigkeit historischer Temperaturaufzeichnungen abzuschätzen, sind doch die Original-Instrumente kaum noch für eine Kalibrierung verfügbar.

Präzision

Der zweite Aspekt ist die Präzision, mit der die Temperaturen aufgezeichnet werden, sowie die sich daraus ergebende Anzahl signifikanter Ergebnisse, wenn die Berechnungen durchgeführt werden wie etwa das Ableiten von Mittelwerten und Anomalien. Dies ist der wichtigste Teil dieser Kritik.

Falls eine Temperatur mit dem nächsten Zehntel eines Grades aufgezeichnet wird, lautet die Konvention, dass deren Wert gerundet oder geschätzt wird. Das heißt, eine Temperaturmessung mit einem Wett von 98,6°F kann zwischen 98,55°F und 98,64°F liegen.

Die allgemeine Faustregel für Addition/Subtraktion lautet, dass rechts vom Komma nicht mehr signifikante Zahlen in der Summe auftauchen als die Anzahl signifikanter Angaben in der am wenigsten präzisen Messung. Bei Multiplikation/Division lautet die allgemeine Faustregel, dass höchstens eine zusätzliche signifikante Zahl im Ergebnis auftaucht im Vergleich mit dem Multiplikanden, welche die am wenigsten signifikanten Angaben enthält. Allerdings folgt man gewöhnlich der Regel, nur so viele signifikante Zahlen zu erhalten wie der am wenigsten präzise Multiplikand enthält. (Eine ausführliche Erklärung all dieser Regeln steht hier).

Anders als in einem Fall mit ganzen Zahlen lässt eine Reduktion der Anzahl signifikanter Angaben bereits um nur eine Messung in einer Reihe die Unsicherheit im Mittel zunehmen. Intuitiv könnte man vermuten, dass die Herabsetzung der Präzision einer oder mehrerer Messungen in einem Datensatz auch die Präzision der Ergebnisse mathematischer Berechnungen reduzieren sollte. Man nehme zum Beispiel an, dass jemand das arithmetische Mittel der Zahlen 50; 40,0 und 30,0 berechnen will, wobei die nach dem Komma stehenden Nullen die letzte signifikante Angabe sind. Die Summe der drei Zahlen beträgt 120 mit drei signifikanten Angaben. Dividiert man durch die ganze Zahl 3 (exakt) erhält man 40,0 mit einer Unsicherheit bei der nachfolgenden Stelle von ± 0,05.

Wie ist das nun aber, wenn wir die implizite Unsicherheit aller Messungen berücksichtigen? Man beachte zum Beispiel, dass im zuvor untersuchten Satz alle Messungen eine implizite Unsicherheit enthalten. Die Summe von 50 ±0,5; 40,0 ±0,05 und 30 ±0,05 beträgt 120,0 ±0,6. Zwar ist das nicht gerade sehr wahrscheinlich, doch könnte es sein, dass alle diese Fehler das gleiche Vorzeichen haben. Das bedeutet, dass der Mittelwert so klein sein kann wie 39,80 oder so groß wie 40,20. Das heißt, dass die Zahl 40,00 ±0,20 abgerundet werden sollte auf 40,0 ±0,2. Vergleicht man diese Ergebnisse mit den zuvor erhaltenen, kann man erkennen, dass es eine Zunahme der Unsicherheit gibt. Die potentielle Differenz zwischen den Grenzen des mittleren Wertes können zunehmen, wenn mehr Daten gemittelt werden.

Es ist vor allem unter Begutachtern [surveyors] allgemein bekannt, dass die Präzision multipler, gemittelter Messwerte invers variiert mit der Quadratwurzel der Anzahl der verwendeten Messungen. Mittelung neigt dazu, den Zufallsfehler bei der Rundung zu entfernen, wenn man einen festen Wert misst. Allerdings sind die Schwächen hier, dass alle Messungen mit dem gleichen Gerät durchgeführt werden müssen, mit dem gleichen festen Parameter wie etwa einer Winkeländerung mit einem Durchgang [an angle turned with a transit]. Außerdem warnt Smirnoff (1961): „bei einer niedrigen Größenordnung der Präzision wird aus wiederholten Messungen keine Zunahme der Genauigkeit folgen“. Dies führt er noch weiter aus mit der Bemerkung: „Implizit ist hier, dass es ein Limit gibt, wie viel der Präzision überhaupt zunehmen kann, während die Definition des Standardfehlers des Mittels die Standardabweichung der Mitglieder ist dividiert durch die Quadratwurzel der Anzahl der Mitglieder. Dieser Prozess kann nicht unendlich oft wiederholt werden, um irgendeine gewünschte Präzision zu erhalten!“

Während mittels einer Vielzahl von Beobachtern ein systematischer Bias dieser Beobachter eliminiert werden kann, sind die anderen Erfordernisse weniger vernachlässigbar. Unterschiedliche Geräte werden unterschiedliche Genauigkeiten aufweisen und können die gemittelten Werte ungenauer machen.

Genauso sagt die Messung unterschiedlicher Betrachtungswinkel einem nichts über Genauigkeit und Präzision eines bestimmten interessierenden Betrachtungswinkels. Folglich sagt einem die Messung multipler Temperaturen über eine Reihe von Stunden oder Tagen nichts über die Unsicherheit der Temperaturwerte an einer gegebenen Stelle zu einer bestimmten Zeit, und es kann auch nichts zur Eliminierung von Rundungsfehlern beitragen. Allerdings sind Temperaturen kurzlebig, und man kann die Temperatur irgendwann später nicht noch einmal messen. Grundsätzlich hat man nur eine Gelegenheit, die präzise Temperatur an einer Stelle zu einer bestimmten Zeit zu bestimmen.

Das Automated Surface Observing System (ASOS) der NOAA verfolgt einen unkonventionellen Weg der Behandlung umgebender Temperaturdaten. Im User’s Guide heißt es in Abschnitt 3.1.2:

Einmal pro Minute berechnet die ACU das 5-minütige Mittel der Umgebungstemperatur und des Taupunktes aus den 1-Minute-Beobachtungen … Diese 5-Minuten-Mittel werden zum nächstgelegenen Grad Fahrenheit gerundet, zum nächsten 0,1 Grad Celsius konvertiert und einmal pro Minute ausgegeben als das 5-Minuten-Mittel der umgebenden Temperatur und des Taupunktes…“.

Dieses automatisierte Verfahren wird mit Temperatursensoren durchgeführt, welche geeicht sind auf einen RMS-Fehler von 0,5°C, einen Maximum-Fehler von ±1,0°C und einer Auflösung von 0,06°C in den wahrscheinlichsten Temperatur-Bandbreiten, die in den kontinentalen USA angetroffen werden. Die Angabe der gerundeten Temperatur in Grad Celsius, wie oben aus dem Zitat hervorgehend, impliziert eine Präzision von 0,1°C, obwohl nur 0,6 ±0,3°C gerechtfertigt sind. Damit wird eine Präzision impliziert, die 3 bis 9 mal größer ist als sie ist. In jedem Falle ist selbst bei der Verwendung modernster Instrumente die Angabe von zwei oder mehr signifikanter Ziffern rechts vom Komma bei Anomalien der verfügbaren Temperaturdaten nicht garantiert!

Konsequenzen

Diese Dinge werden besonders wichtig, wenn die Temperaturdaten aus unterschiedlichen Quellen stammen, wobei unterschiedliche Instrumente mit variierender Genauigkeit und Präzision verwendet werden, um alle verfügbaren globalen Temperaturen zusammenzubringen und zu konsolidieren. Auch werden sie wichtig beim Vergleich historischer mit modernen Daten und besonders bei der Berechnung von Anomalien. Ein bedeutendes Problem mit historischen Daten ist, dass Temperaturen typischerweise nur in ganzen Zahlen gemessen wurden (wie es bei modernen ASOS-Temperaturen der Fall ist!). Folglich weisen die historischen Daten geringe Präzision (und unbekannte Genauigkeit) auf, und die oben genannte Regel für die Subtraktion kommt ins Spiel, wenn man berechnet, was gemeinhin Temperaturanomalie genannt wird. Das heißt, die Daten werden gemittelt, um eine so genannte Temperatur-Grundlinie [einen Temperatur-Referenzwert] zu berechnen, typischerweise für einen Zeitraum von 30 Jahren. Dieser Referenzwert wird von den aktuellen Daten subtrahiert, um eine Anomalie zu definieren. Ein Weg zur Umgehung dieser Subtraktion ist es, das beste verfügbare historische Mittel zu berechnen und danach so zu definieren, als wären genauso viele signifikante Angaben eingegangen wie in moderne Daten. Dann ist es nicht erforderlich, moderne Daten zu beschneiden und zu runden. Man kann dann legitimerweise sagen, wie sich die derzeitigen Anomalien darstellen hinsichtlich des definierten Referenzwertes, obwohl nicht offensichtlich ist, ob die Differenz statistisch signifikant ist. Unglücklicherweise macht man sich nur etwas vor, wenn man glaubt, dass diese Anomalien irgendetwas darüber aussagen können wie aktuelle Temperaturdaten im Vergleich zu historischen Temperaturdaten dastehen, wenn die Variationen nur rechts des Kommas zu finden sind!

Bezeichnend für das Problem ist, dass die von der NASA veröffentlichten Daten bei Anomalien am Ende des 19. Jahrhunderts und aktuelle Anomalien die gleiche implizite Präzision aufweisen (±0,005°C). Der Charakter der Datentabelle mit der Eingabe von 1 bis 3 Ziffern ohne Komma zeigt, dass die Aufmerksamkeit für signifikante Angaben wenig Berücksichtigung gefunden hat. Sogar noch ungeheuerlicher ist die Repräsentation einer Präzision von ±0,0005°C für Anomalien in einem Wikipedia-Beitrag, in welchem die NASA als Quelle angegeben wird.

Idealerweise sollte man eine kontinuierliche Aufzeichnung von Temperaturen über einen Zeitraum von 24 Stunden haben und die Fläche unter dem Temperatur-Zeit-Graphen integrieren, um eine wahre mittlere tägliche Temperatur zu erhalten. Allerdings ist diese Art einer Temperaturreihe nur selten, was besonders für ältere Daten gilt. Folglich müssen wir mit den Daten, die wir haben, alles in unserer Macht Stehende tun, was oftmals eine Bandbreite von Tag zu Tag ist. Zieht man die tägliche Höchst- bzw. Tiefsttemperatur heran und mittelt diese separat, gibt dies einen Einblick, wie sich Temperaturen an einer Station mit der Zeit ändern. Beweise zeigen, dass die Höchst- und Tiefsttemperaturen sich während der letzten 100 Jahre nicht in gleicher Weise geändert haben – bis vor Kurzem, als die Tiefsttemperaturen rascher gestiegen sind als die Höchsttemperaturen. Das bedeutet, sogar auch für langfristig gut betreute Wetterstationen, dass wir kein wahres Mittel der Temperatur mit der Zeit haben. Im besten Falle haben wir einen Mittelwert der täglichen Höchst- und Tiefsttemperaturen. Diese zu mitteln erzeugt ein Artefakt, bei welchem Informationen verloren gehen.

Wenn man ein Mittel berechnet zum Zwecke einer wissenschaftlichen Analyse wird diese konventionell mit einer Standardabweichung gezeigt, also einer Maßzahl der Variabilität der individuellen Einzelwerte innerhalb der Stichprobe. Ich habe bis heute noch keine einzige veröffentlichte Standardabweichung gesehen im Zusammenhang mit jährlichen globalen Temperatur-Mittelwerten. Wendet man jedoch das Theorem von Tchebysheff und die Empirische Regel (Mendenhall 1975) an, können wir mit einer konservativen Schätzung der Standardabweichung für globale Mittelwerte aufwarten. Das heißt, die Bandbreite der globalen Temperaturen sollte angenähert vier mal die Standardabweichung sein (R_ange ≈ ±4s). Bedenkt man jetzt, dass sommerliche Temperaturen in der Wüste etwa 130°F [ca. 54°C] und winterliche Temperaturen in der Antarktis -120°F [ca. -84°C] erreichen können, ergibt sich eine jährliche Bandbreite der Temperatur auf der Erde von mindestens 250°F [ca. 140 K] und damit eine geschätzte Standardabweichung von etwa 31°F [ca. 17 K]! Weil es in Wüsten und den Polargebieten kaum Messungen gibt, ist es wahrscheinlich, dass die Bandbreite (und damit die Standardabweichung) größer ist als meinen Vermutungen zufolge. Man sollte intuitiv den Verdacht haben, dass die Standardabweichung für das Mittel hoch ist, liegen doch nur wenige der globalen Messungen nahe dem Mittelwert! Und trotzdem werden globale Anomalien allgemein mit signifikanten Angaben rechts vom Komma präsentiert! Die Mittelung der jährlichen Höchsttemperaturen separat von den jährlichen Tiefstwerten würde die geschätzte Standardabweichung deutlich reduzieren, aber es würde immer noch nicht die Präzision rechtfertigen, von der allgemein die Rede ist. Diese geschätzte Standardabweichung sagt uns möglicherweise mehr über die Häufigkeitsverteilung von Temperaturen als die Präzision, die bzgl. des Mittels bekannt ist. Sie sagt, dass möglicherweise etwas mehr als zwei Drittel der aufgezeichneten Temperaturen zwischen -26°F und +36°F liegen [ca. zwischen -32°C und +2°C]. Weil der Zentralwert [median] dieser Bandbreite 5,0°F[*] beträgt und die allgemein akzeptierte mittlere globale Temperatur bei etwa 59°F [ca. 15°C], zeigt dies, dass es noch einen langen Schwanz bei dieser Verteilung gibt, was die Schätzung des Zentralwertes hin zu einer niedrigeren Temperatur verzerrt.

[*Die Umrechnung der absoluten Fahrenheit-Temperaturen in Grad Celsius ist einfach, aber der angegebene Zentralwert von 5°F lässt sich nicht umrechnen. Nehme ich den Zentralwert der Celsius-Angaben, komme ich auf einen Wert bei 15 K. Wahrscheinlich unterläuft mir hier ein logischer Denkfehler, aber ich bekenne, dass ich ihn nicht finden kann. Anm. d. Übers.]

Summary

Zusammengefasst lässt sich sagen, dass es zahlreiche Arten der Datenbehandlung gibt, welche Klimatologen allgemein ignorieren. Sie kompromittieren ernsthaft die Wahrhaftigkeit der Behauptungen über rekordhohe Mitteltemperaturen und reflektieren eine ärmliche [poor] Wissenschaft. Die statistische Signifikanz von Temperaturunterschieden 2 oder sogar 3 Stellen nach dem Komma ist höchst fragwürdig. Die Anwendung des Verfahrens der Berechnung des Standardfehlers des Mittelwertes, um dessen Präzision zu verbessern, wird nicht gerechtfertigt durch das Entfernen von Zufallsfehlern, weil es keinen festgelegten einzelnen Wert gibt, um den sich die Zufallsfehler verteilen. Das globale Mittel ist ein hypothetisches Konstrukt, welches in der Natur nicht existiert. Stattdessen ändern sich Temperaturen; sie erzeugen variable Fehler systematischer Art. Echte Wissenschaftler sind besorgt hinsichtlich der Größenordnung und des Ursprungs der unvermeidlichen Fehler in ihrem Messungen.

References

Mendenhall, William, (1975), Introduction to probability and statistics, 4^th ed.; Duxbury Press, North Scituate, MA, p. 41

Smirnoff, Michael V., (1961), Measurements for engineering and other surveys; Prentice Hall, Englewood Cliffs, NJ, p.181

Taylor, John R., (1982), An introduction to error analysis – the study of uncertainties in physical measurements; University Science Books, Mill Valley, CA, p.6

Link: https://wattsupwiththat.com/2017/04/12/are-claimed-global-record-temperatures-valid/

Übersetzt von Chris Frey EIKE

Anmerkung: Der Autor hat zu diesem Grundlagen-Artikel einen Folgebeitrag geschrieben, in welchem er diese Erkenntnisse auf die gegenwärtige Mainstream-„Klimaforschung“ überträgt. Dieser befindet sich in der Übersetzung und wird in einigen Tagen ebenfalls hier gepostet. – C. F.