Abartige Klimareaktion im DICE IAM Modell– ein Billionen-Dollar-Fehler?*
[*Vorab: Die Abkürzung IAM wird gleich im nächsten Absatz genannt. Anders ist es bei DICE. Im Beitrag wird immer nur die Abkürzung genannt. Aber bei Wikipedia findet man die Erklärung. Die Abkürzung steht für „Dynamic Integrated Climate-Economy model“. WICHTIG: Es handelt sich auch um ein unübersetzbares Wortspiel. „Dice“ ist das amerikanische Wort für „Würfel“!
Weitere Vorbemerkungen des Übersetzers: Der folgende Beitrag ist überaus theoretischer Natur. Alle Indizes von Formelzeichen sind im Original korrekt niedrig gestellt, was aber hier im Server nicht darstellbar ist. Die Niedrigstellung der Indizes wird daher hier mit dem eingefügten Zeichen „↓“ indiziert.
Außerdem tauchen im Artikel immer wieder Fachbegriffe auf, vor deren Übersetzung ich kapituliere. Sie sind kursiv gesetzt. Da ich als Laie außerdem viele der hier beschriebenen Zusammenhänge inhaltlich nicht verstehe, kann es zu inhaltlichen Fehlern bei der Übersetzung kommen.
Kompliziert wird diese Übersetzung auch dadurch, dass der Autor wie viele andere Wissenschaftler auch versucht, möglichst viel Information in möglichst wenige Sätze zu stecken. Die resultierenden Bandwurm- und Schachtelsätze sind teilweise schwer zu sezieren.
Der Autor geht von der AGW-Hypothese als Tatsache aus.
Ende Vorbemerkungen des Übersetzers.]
Einführung und Summary
Integrated Assessment Models (IAMs) kombinieren einfache Modelle des Kohlenstoff-Kreislaufes sowie der Reaktion des Klimasystems auf Änderungen der atmosphärischen CO2-Konzentration mit Modellen ökonomischen Wachstums, die die Auswirkungen der Einführung einer Kohlenstoff-Steuer enthalten. Sie berechnen den resultierenden sozialen Nutzen nach Abschätzung der Schäden durch den Klimawandel und der Kosten der ergriffenen Maßnahmen – als eine Folge der Kohlenstoff-Steuer – um CO2-Emissionen abzuschwächen. Die optimale, mit der Zeit variierende, von den IAMs berechnete Kohlenstoff-Steuer ist während eines gesamten betrachteten Zeitraumes gleich den sozialen Kosten von Kohlenstoff (SCC). Ergebnisse der IAMs werden von Regierungen bei der Entscheidung herangezogen, welche Höhe die einzuführende Kohlenstoff-Steuer haben muss und/oder welches Ziel von Emissionsreduktionen man anpeilen sollte [i].
In diesem Beitrag geht es hauptsächlich um das DICE, eines der drei IAMs, die von der US-Regierung bei ihrer Abschätzung von SCC [ii] herangezogen werden, und welches von William Nordhaus entwickelt worden war. Er hat ein Kapitel geschrieben, dass eine gute Einführung in IAMs im Allgemeinen sowie DICE im Besonderen [iii] darstellt. Das DICE-Modell teilt den Zeitraum 2010 bis 2309 in 5-Jahre-Schritte, wobei die Kohlenstoff-Steuer ab 2015 variierend gestaltet werden soll. In diesem Beitrag befasse ich mich nur mit der Funktion der DICE-Klimamodule und stelle das übrige Modell nicht in Frage.
Obwohl ich die in das DICE-Modell eingehenden Werte der Gleichgewichts-Klimasensitivität ECS berücksichtige, ebenso wie die Vorübergehende Klimareaktion TCR, deren von dessen Klimamodul berechnete Werte höher als gerechtfertigt ausfallen laut den Best Estimates, die sich auf Messungen des Klimasystems ergeben, stelle ich jene Werte hier nicht in Frage. Allerdings werde ich zeigen, dass das DICE-Klimamodul falsche Ergebnisse dergestalt liefert, dass das Zeitprofil von dessen Temperaturreaktion auf Antriebe inkonsistent ist mit unserem Verständnis des Verhaltens des tatsächlichen Klimasystems, wie es von der gegenwärtigen Generation der CMIP5-Modelle und der atmosphere-ocean general circulation models (AOGCMs) reflektiert und simuliert wird.
Es wurde gezeigt, dass die Entwicklung der globalen Mitteltemperatur in AOGCMs gut repräsentiert werden kann durch ein einfaches 2-Schichten-Modell auf physikalischer Grundlage, wie es im DICE verwendet wird, mit geeigneter Auswahl von Ozean-Tiefenschichten für jede Schicht. Allerdings zeige ich hier, dass die Werte der Parameter des Klimamoduls im DICE mit physikalisch unrealistischen Ozean-Charakteristiken korrespondieren. In dem 2-Schichten-Modell des DICE wird die Oberflächen-Schicht des Ozeans, die als kontinuierlich im Gleichgewicht befindlich mit der Atmosphäre angesehen wird, mit einer Tiefe von 550 m geschätzt, verglichen mit Schätzungen einer Tiefe von 50 bis 150 m auf der Grundlage von Messungen und der Anpassung von 2-Schichten-Modellen an AOGCM-Reaktionen. Die Tiefe der Ozeanschicht im DICE-2-Schichten-Modell ist weniger als 200 m tief, das ist nur ein Bruchteil des Wertes in irgendeinem CMIP5-AOGCM, und sie ist viel schwächer mit der Oberflächen-Schicht gekoppelt. Wenig überraschend erzeugen derartige Parameter ein zeitliches Profil der Temperaturreaktion, welches substantiell von jenem in den AOGCMs und dem 2-Schichten-Modell mit typischen Parameter-Werten abweicht. Als Folge davon überschätzt das DICE signifikant die Temperaturen ab Mitte des 21. Jahrhunderts. Folglich wird auch SCC und die optimale Kohlenstoff-Steuer überschätzt, verglichen mit 2-Schichten-Modellen mit gleichem ECS und TCR, aber mit Parameter-Werten, die eine Temperaturentwicklung ähnlich AOGCM erzeugen.
Falls die Parameter des DICE-Klimamoduls in ihren Standardwerten verändert werden, damit sie konsistent sind mit dem AOGCM-Verhalten sowie tatsächlichen Ozean-Charakteristiken , aber die ECS- und TCR-Werte unverändert belassen werden, zeigt meine Analyse, dass SCC und die Optimum-Kohlenstoffsteuer einer substantiell niedrigeren Trajektorie folgen (bis 2110 um ein Viertel bis ein Drittel weniger). Und das mit größeren CO2-Emissionen, aber einem geringeren Spitzen-Niveau der Erwärmung. Der gegenwärtige Nutzwert wird um bis zu 19 Billionen Dollar verbessert, abhängig davon, welcher alternative Parameter-Satz herangezogen wird. Verwendet man diese Parameter-Sätze, resultiert ein Nutz-Verlust der Größenordnung von 1 Billion Dollar aus der Einführung der höheren Kohlenstoff-Steuer, die optimal ist, wenn man die Standardeinstellungen des DICE-Klimamoduls anstatt ihrer eigenen verwendet. [Original: When using these parameter sets, a loss of utility of the order of $1 trillion results from imposition of the higher carbon tax that is optimum when using the DICE climate module standard settings instead of their own, lower, optimum carbon tax]. Das Profil der Klima-Reaktion in FUND[iv] und in PAGE,[v], also den beiden anderen, von der US-Regierung verwendeten IAMs zur Abschätzung des SCC, erscheinen ähnlich ungeeignet, das heißt, sie überschätzen ebenfalls SCC.
Das Klimamodul in der derzeitigen Version von DICE
Ich verwendete die jüngste Version von DICE, also DICE-2013R (April 2014), also die geophysikalischen Module, von denen es heißt, zum größten Teil konsistent zu sein mit dem AR 5 des IPCC [vi]. Allerdings enthält die Excel-Version zum Herunterladen [vii] keine Angabe, wie oft Parameter überarbeitet worden sind, die in der primären Version DICE2013Rv2 des Modells vom Oktober 2013 vorgenommen worden sind, jedenfalls dessen Manual zufolge [viii]. Von besonderer Relevanz zu dessen Klimareaktion sind eine Reduktion des falschen verwendeten ECS von 3,2°C auf 2,9°C sowie Modulationen bei anderen Klimamodul-Parametern. Ich habe diese Änderungen eingearbeitet, und Parameter-Überarbeitungen in anderen Teilen, die Auswirkungen auf Emissionen und SCC haben, stehen in einer aktualisierten Excel-Version, die ich als DICE-2013Ra bezeichne [ix]. Im Manual ist auf Seite 18 zu lesen, dass eine Änderung eines Klimamodul-Parameters [x] vorgenommen worden war, um [den Wert der] kurzlebigen Temperatur-Sensitivität zu erhalten, der laut einer Schätzung einer Regressionsanalyse bei 1,70°C liegt. Anderswo wird bestätigt [xi], dass diese Sensitivität den gleichen Wert haben soll wie die TCR in AOGCMs, welcher die Zunahme der globalen mittleren Temperatur (GMST) am Ende eines Zeitraumes von 70 Jahren ist, beginnend vom Gleichgewicht aus, während dessen die CO2-Konzentration um 1% pro Jahr steigt und sich damit verdoppelt.
Das DICE-Klimamodul repräsentiert ein gobales 2-Schichten-Standard-Klimamodell [xii] [xiii], in welchem sich die Atmosphäre im kontinuierlichen Gleichgewicht befindet mit einer an der Oberfläche durchmischten Schicht des Ozeans, in dem Wärme mit der Tiefsee ausgetauscht wird mit einer Rate proportional zur Temperaturdifferenz dazwischen. Dieses einfache Modell wird vollständig definiert durch Spezifizierung des ECS, die Wärmekapazitäten C↓SO und C↓DO der Oberfläche bzw. der Tiefsee und dem Proportionalitäts-Koeffizienten F↓SD zwischen der Rate des Wärmeaustausches zwischen den Schichten und dem Temperatur-Differential zwischen den Schichten [xiv]. Alternativ wird der Wert von F↓SD einheitlich festgelegt, falls TCR des Modells ebenso spezifiziert ist wie ECS.
Charakteristika von 2-Schichten-Klimamodellen
Die mit der Zeit variierende Änderung von T(t) in GMST im Modell als Reaktion auf eine Stufen-Änderung der Strahlungsantriebe – wie etwa eine Änderung durch einen sprunghaften Anstieg der atmosphärischen CO2-Konzentration – wird gegeben durch die gewichtete Summe von zwei Exponentialfunktionen mit den Zeitkonstanten τ↓1 and τ↓2:
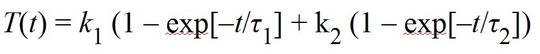
Die Sensitivitäts-Faktoren k↓1 und k↓2 bestimmen, wie die finale Gleichgewichtsreaktion von GMST (zu der sie sich summieren) geteilt wird zwischen zwei Reaktionen von Komponenten mit unterschiedlichen Zeitkonstanten. Eine Ableitung der mathematische Beziehungen zwischen den physikalischen Parametern des 2-Schichten-Modells und der daraus resultierenden exponentiellen Funktion der Zeitkonstanten und Sensitivitäts-Faktoren wird von Berntsen und Fuglestvedt (2008) gegeben [xv]. Allgemein gilt, dass bei gegebenen Werten von ECS und F↓SD die Wärmekapazität der durchmischten Ozean-Oberflächenschicht, C↓SO, welche proportional zu seiner Tiefe ist, sich stark positiv auswirkt auf den Wert von τ↓1, während diejenige der Tiefsee C↓DO stark τ↓2 beeinflusst. Die relativen Werte von k↓1 und k↓2 werden stark durch F↓SD beeinflusst. Wenn man 2-Schichten-Modelle konstruiert, wird die Mächtigkeit der Oberflächenschicht, die sich im Gleichgewicht mit der Atmosphäre befindet, mit 70 bis 120 m angesetzt, gemittelt über das Gebiet der Ozeane. Dies korrespondiert in etwa mit Schätzungen der Tiefe der durchmischten Schicht [xvi]. Während die mittlere Tiefe der Ozeane etwa 3700 m beträgt, kann die effektive Tiefe für die Zwecke eines 2-Schichten-Modells geringer sein infolge des geringeren Austausches unterhalb der Thermokline (deren effektive Tiefe sich in der Größenordnung um 1000 m bewegt). Konsistent mit diesen charakteristischen Ozean-Tiefen erwartet man, dass τ↓1 eine relativ kurze Zeitspanne umfasst – unter zehn Jahre – und τ↓2 eine lange Periode – über 100 Jahre.
Obwohl das 2-Schichten-Klimamodell sehr einfach ist, hat sich herausgestellt, dass die damit erzeugte 2-exponential response in der Lage war – mit geeigneter Auswahl von Parametern – das GMST-Verhalten von AOGCMs bemerkenswert gut zu repräsentieren [xvii]. Abbildung 1 unten, also die Abbildung 2 von Caldeire und Myhrvold (2013; xviii) zeigt, wie gut 2-exponential fits (blaue Linien) für CMIP5-Modelle sind. Deren Untersuchung basierte auf den Ergebnissen von Simulationen, in denen die atmosphärische CO2-Konzentration abrupt vervierfacht worden war. Diese ergeben ein sehr klares Bild des charakteristischen Zeitprofils der Modellreaktion auf eingegebene Antriebe. Die mit diesen Simulationen erreichten 2-exponential fits passen auch exzellent zum GMST-Verhalten der korrespondierenden Modelle während ramp-forcing-Simulationen über 140 Jahre, wobei die CO2-Konzentration um 1% pro Jahr zunehmen soll.
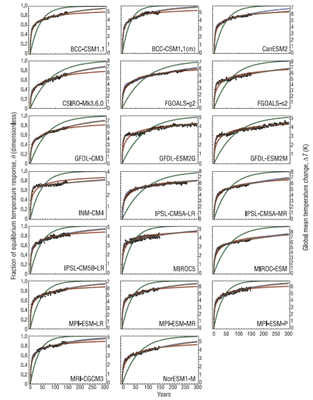
Abbildung 1: GMST-Änderungen in verschiedenen CMIP5-Modellen nach einer abrupten Vervierfachung der CO2-Konzentration zum Zeitpunkt Null (schwarze Punkte), und wie sie von verschiedenen einfachen Modellen mit best-fit parameter-Werten nachgebildet werden. Die blauen Linien repräsentieren Fits an ein C, wie es von einem 2-Schichten-Modell vorgegeben wird. In den meisten Fällen überlappen sie sich mit den braunen Linien des 3-exponential fit. Die Linien in Olivgrün stehen für 1-exponential fits; die roten Linien für Fits an ein 1D Diffusionsmodell.
Konsistent mit physikalisch begründeten Erwartungen kamen Caldeira und Myhrvold zu dem Ergebnis, dass die Werte von τ↓1 und τ↓2, die den besten Fit geben, in Bandbreiten variierten zwischen 2,4 bis 7,4 bzw. 109 bis 463 Jahren, jedenfalls dem involvierten CMIP5-Modell zufolge. Die impliziten Werte von C↓SO und C↓DO korrespondieren mit der Ozean-Oberfläche sowie Tiefenschichten zwischen 64 bis 150 m bzw. 768 bis 3313 m [xix]. Eine andere Studie, bei der CMIP5 AOGCMs involviert waren, kam zu ähnlichen Ergebnissen. Sie gab auch Werte für F↓SD mit einer Bandbreite von 0,5 und 1,16 Wm² pro K [xx]. Genauso haben Boucher und Reddy (2008) ein two-exponential model an das CMIP3 HadCM3-Modell angepasst [fitted] und erhielten Zeitkonstanten von 8,4 Jahren für τ↓1 und 409,5 Jahren für τ↓2, mit Sensitivitäts-Parametern, die einem ECS von 3,90°C und einem TCR von 2,17°C gleichen [xxi]. Ihr angepasstes Modell fand Eingang in den AR5 [xxii]. Dessen implizierte Werte von C↓SO und C↓DO korrespondieren mit der Ozeanoberfläche und Tiefenschichten von 70 m bzw. 3000 m. Die Ozeanschichten-Tiefenkombinationen von Boucher & Reddy und Berntsen & Fuglestvedt decken Vieles ab, was physikalisch plausibel ist (mit Berücksichtigung der Tiefen der durchmischten Ozean-Oberflächenschicht, dem Ozean darunter und der Thermokline). Dies ist auch erforderlich, um zum Verhalten des CMIP5-Modells zu passen. Außerdem verwendete ich Wertekombinationen aus C↓SO und C↓DO aus jenen beiden Studien, um 2-Schichten-Modelvarianten als Referenz zu definieren, und verglich deren GMST-Reaktionen mit denen von DICE-2013Ra. Während die exponentiellen Zeitkonstanten für jede dieser 2-Schichten-Modellvarianten mit den spezifizierten Werten von ECS und TCR variierten, blieben die Wärmekapazitäten der Ozeanschichten unverändert.
Vergleich der Reaktion des DICE 2-Schichten-Modells mit jener der beiden Modellvarianten
Um objektiv die GMST-Reaktionen der verschiedenen Parametrisierungen des 2-Schichten-Modells vergleichen zu können, ist es angemessen, die gleichen ECS- und TCR-Werte für alle davon zu spezifizieren. Die Unterschiede hinsichtlich der Reaktion hängen dann lediglich noch ab von den eingehenden Tiefenschichten [deep layer depths] und der Ozeanoberfläche.
Alle Parameter, die TCR beeinflussen, haben in DICE-2013Ra die gleichen Werte wie in DICE-2013-Rv2. Obwohl Nordhaus feststellt, dass die geschätzte TCR von DICE-2013Rv2 1,7°C beträgt, ist der Wert, den ich für DICE-2013Ra berechne, nur 1,57°C. Dies, indem ich eine linear forcing ramp von einer präindustriellen Gleichgewichtslage anwende [xxiv]. Der Grund für die Ungenauigkeit der TCR-Festsetzungen in DICE-2013R ist unbekannt; möglicherweise ist er in dem Regressionsmodell zu suchen, das für die Abschätzung der TCR des Modells ungeeignet ist.
Dem entsprechend setzte ich die Werte von F↓SD in den Referenz-Varianten von 2-Schichten-Modellen mit der Ozean-Oberflächen-Tiefe und den deep layer depths so, dass sich ein TCR-Wert von 1,57°C ergibt, wenn man ihn in DICE-2013Ra verwendet. Passt dies zu den Original-Einstellungen des Modells, erhält man den gleichen ECS-Wert von 2,9°C. Dann berechnete ich für einen Zeitraum von über 250 Jahren die GMST-Reaktion einer jeden 2-Schichten-Modellvariante bei einer abrupten Verdoppelung der CO2-Kinzentration; die Ergebnisse zeigt Abbildung 2. Das Aussehen der Reaktion von DICE-2013a ist deutlich unterschiedlich zu jenen Reaktionen der beiden anderen Modellvarianten. Das Aussehen der Linien der Varianten von Boucher & Reddy sowie Berntsen & Fuglestvedt sind ähnlich den blauen 2-exponential curves und den tatsächlichen AOGCM-Reaktionen in Abbildung 1. Die DICE-2013a-Linie hat dagegen ein ziemlich unterschiedliches Aussehen – eine näher der grünen 1-exponential curves in Abbildung 1 [xxv]. Nach 10 Jahren haben die Reaktionen von CMIP5 AOGCM in Abbildung 1 zwischen 38% und 61% ihrer geschätzten ultimativen Gleichgewichts-Erwärmung erreicht. Nach 100 Jahren haben sie zwischen 60% und 86% ihrer ultimativen Gleichgewichts-Erwärmung erreicht. Die 10-Jahre-Prozentzahlen für die Modelle von Boucher & Reddy sowie Berntsen & Fuglestvedt betragen jeweils 44% und 51%, nach 100 Jahren 67% und 61%. Diese Werte liegen innerhalb der Bandbreiten von den AOGCMs in Abbildung 1. Allerdings liegen die 10- und 100-Jahre-Prozentzahlen von DICE-2013Ra mit jeweils 22% und 89% außerhalb der AOGCM-Bandbreiten.
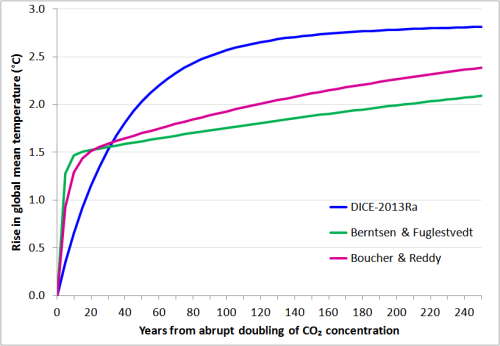
Abbildung 2: GMST-Reaktion jeder 2-Schichten-Modellvariante bei einer abrupten Verdoppelung der CO2-Konzentration.
Der Grund für die anomal aussehende GMST-Reaktion in DICE2013Ra ist, dass dessen 2-Schichten-Klimamodell physikalisch unrealistische Ozean-Tiefenschichten [ocean layer depths] enthält. Dessen implizierter C↓SO-Wert ist gleich einer mittleren Tiefe der Ozean-Oberflächenschicht von 553 m – vier- bis achtmal höher als für die beiden Referenz-Modellvarianten und weitaus größer als die Tiefe der Schicht, die sich fast im Gleichgewicht mit der Atmosphäre befindet. Der DICE-2013a-C↓DO-Wert gilt für eine mittlere Tiefe der ozeanischen Tief-Schicht von 191 m – also nur etwa ein Sechstel bis ein Zwölftel der Werte für die beiden anderen Modellvarianten. DICE-2013Ra hat auch einen viel niedrigeren Koeffizienten des Wärmeaustausches zwischen der Oberflächen-Schicht und den Schichten der Tiefsee: deren F↓SD-Wert von 0,088 Wm² pro K beträgt weniger als 10% des Wertes in den anderen beiden Modellvarianten (welche fast die gleichen F↓SD-Werte aufweisen).
Als Folge der sehr geringen Kopplung zwischen Oberfläche und Tiefsee ist die Zeitkonstante des zweiten Exponential-Terms von DICE-2013Ra mit 216 Jahren vernünftig, trotz der geringen Dicke der Tiefsee-Schicht. Allerdings ist die erste exponentielle Zeitkonstante τ↓1 mit 36 Jahren außerordentlich hoch und liegt weit außerhalb der Bandbreite von CMIP5 mit 2,4 bis 7,4 Jahren, was von Caldeira und Myhrvold gefunden worden war. Für die Referenz-Modellvarianten beträgt τ↓1 5 Jahre nach Boucher & Reddy sowie 2,5 Jahre nach Berntsen & Fuglestvedt. In DICE-2013Ra wird die GMST-Reaktion dominiert von jener des ersten Exponential-Terms; infolge der schwachen Kopplung zwischen den Schichten trägt die längere Zeitkonstante, also der zweite Term, nur 9% zur Gesamt-Gleichgewichts-Erwärmung bei [xxvi]. Dies liegt weit unterhalb der Bandbreite von 33% bis 61%, wie sie von Caldeira & Myhrvold für CMIP5-Modelle berichtet wird und ist vergleichbar mit Werten von etwa 50% der beiden 2-Schichten-Modellvarianten sowohl von Boucher & Reddy als auch von Berntsen & Fuglestvedt.
Relevante Details aller drei 2-Schichten-Modellvarianten zeigt Tabelle 1:
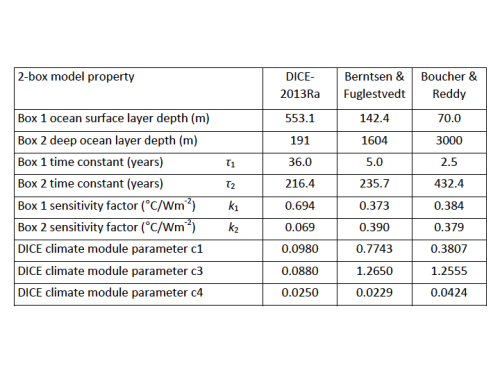
Tabelle 1: Eigenschaften jeder 2-Schichten-Modellvariante, alle mit ECS bei 2,9°C und TCR bei 1,57°C. Die Werte korrespondieren mit den vorgegebenen DICE-2013Ra-Parametern [xxvii].
Die Auswirkung auf SCC und optimale Kohlenstoff-Steuer der verschiedenen 2-Schichten-Klimamodelle
Die sonderbare GMST-Reaktion des DICE-2013Ra-2-Schichten-Klimamodells erfolgt viel langsamer als jene der beiden anderen, physikalisch plausibleren alternativen 2-Schichten-Modellvarianten und als CMIP5-Modelle. Aber deren Neigung nimmt viel langsamer ab. 35 Jahre nach Applikation eines Antriebs ist die DICE-2013Ra-Temperaturreaktion auf einen aufgezwungenen Antrieb größer als die der alternativen 2-Schichten-Modellvarianten mit identischen ECS- und TCR-Werten, und im 100. Jahr liegt sie deutlich über ihren Reaktionen.
Die Schlüsselfrage lautet, welche Auswirkung die variierende Gestalt dieser drei Klimareaktions-Funktionen mit identischen Werten sowohl für ECS als auch für TCR auf SCC haben, auf die CO2-Emissions-Szenarien, die nach Einführung einer Optimum-Kohlenstoff-Steuer folgen. Um die Kohlenstoff-Steuer optimieren zu können mittels des Standard-Excel-Programms, welches unzuverlässig ist bei der Optimierung von mehr als nur einigen wenigen Parametern, spezifiziere ich die Kohlenstoff-Steuer mittels eines 4-Parameter-Modells [xxviii]. Ich lasse die Werte der Einsparungsraten bei dem Excel-Modell unverändert; die optimale Einsparungsrate wird kaum beeinflusst durch Variationen der optimalen Kohlenstoff-Steuer.
Abbildung 3 zeigt die resultierenden optimierten Werte der Kohlenstoff-Steuer für jede 2-Schichten-Klimamodell-Variante. Die Optimierung wird ab 2015 appliziert; der initiale Kohlenstoff-Preis beträgt in allen Fällen 1 Dollar. Die Spitzenwerte treten auf, wenn der steigende SCC den backstop price erreicht, ein ursprünglich sehr hoher Preis, der mit der Zeit sinkt, wobei jede geforderte Größe der Emissionsreduktion als möglich angenommen wird [xxix]. Nach 2150 nimmt der Kohlenstoff-Preis in allen Fällen weiter ab mit dem backstop price [xxx]. Bis 2110 beträgt die optimale Kohlenstoff-Steuer für die 2-Schichten-Modellvariante nach Berntsen & Fuglestvedt zwei Drittel und jene für die Variante nach Boucher & Reddy drei Viertel des Wertes nach DICE-2013Ra [xxxi]. Das sind substantielle Reduktionen.
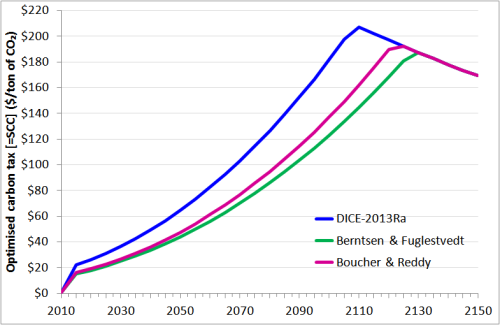
Abbildung 3: DICE-2013Ra-Optimum-Kohlenstoff-Steuer-Profil für jede 2-Schichten-Modellvariante.
Die Auswirkungen der unterschiedlichen Niveaus der Kohlenstoff-Steuer auf CO2-Emissionen, CO2-Konzentration und GMST
Eine niedrigere Kohlenstoff-Steuer impliziert, dass die optimalen Emissionen höher sind. Abbildung 4 zeigt das Profil von CO2-Emissionen in jedem Fall, der sich aus einer Einführung der korrespondierenden optimalen Kohlenstoff-Steuer ergibt, und zum Vergleich für den grundlegenden Fall, dass die Kohlenstoff-Steuer nur langsam steigt von ihrem Niveau 2010 [xxxii]. Die kumulativen Emissionen von 2010 bis 2050 in den drei Fällen betragen 621, 790 und 858 GT CO2 – alle weitaus weniger als die 2.222 GT CO2 im Grundlagen-Fall. Allerdings sind die Emissionen nach der 2-Schichten-Modellvariante nach Berntsen & Fuglestvedt um 38% höher, nach dem von Boucher & Reddy 27% höher als auf der Grundlage des DICE2013Ra-2-Schichten-Modells.
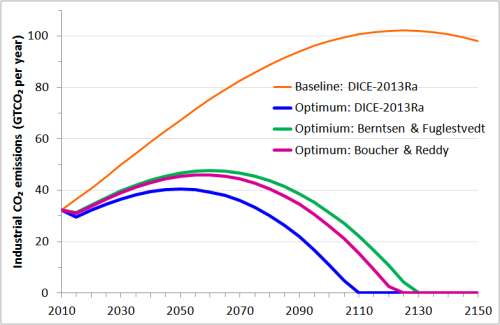
Abbildung 4: DICE-2013Ra-CO2-Emissionen mit einer Kohlenstoff-Steuer optimiert für jede 2-Schichten-Modellvariante.
Die korrespondierenden atmosphärischen CO2-Konzentrationen zeigt Abbildung 5, und zwar bis zum Jahr 2295. Sie erreichen einen um 60 ppm höheren Spitzenwert im Falle von Berntsen & Fuglestvedt als mit dem 2-Schichten-Klimamodell von DICE-2013Ra. Dies reflektiert die substantiell höheren kumulativen CO2-Emissionen, aber nur bei 51% des baseline case peak level.
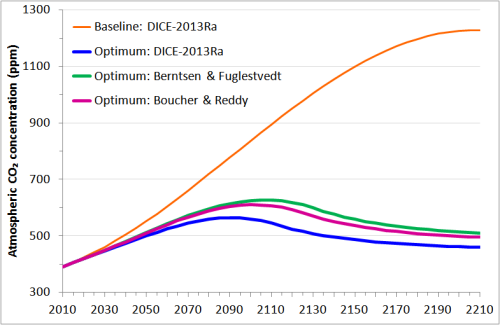
Abbildung 5: CO2-Konzentration nach DICE-2013Ra mit einer Kohlenstoff-Steuer, die optimiert ist nach jeder 2-Schichten-Modellvariante.
Nun könnte man denken, dass mit den kontinuierlich höheren CO2-Konzentrationen der 2-Schichten-Modellvarianten nach Berntsen & Fuglestvedt bzw. Boucher & Reddy als dem eigenen 2-Schichten-Klimamodell in DICE-2013Ra die resultierende Zunahme von GMST in ihren Fällen größer wäre. Tatsächlich ist dies nicht so bis zum Jahr 2300. Tatsächlich ist der Spitzen-GMST-Anstieg merklich höher mit dem ursprünglichen DICE-2013Ra-Klimamodell, bei 3,0°C im Jahre 2120, zu welcher Zeit der Anstieg nach Boucher & Reddy 2,5°C und nach Berntsen & Fuglestvedt 2,3°C beträgt. Obwohl in jenen beiden Fällen GMST ultimativ weiter steigt, bleibt er in beiden Fällen unter 2,8°C für mindestens eintausend Jahre. Zum Vergleich, im baseline case beträgt die Spitzenzunahme von GMST über 6°C.
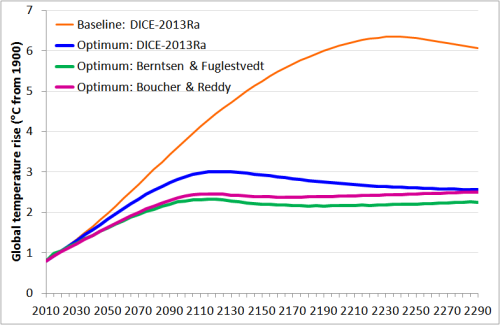
Abbildung 6: DICE-2013Ra GMST-Änderung mit der Kohlenstoff-Steuer optimiert für jede 2-Schichten-Modellvariante
Diskussion und Schlussfolgerungen
Ich habe gezeigt, dass die 2-box climate temperature response function in DICE-2013R unsinnig ist, basiert sie doch auf der Tiefe der Ozean-Oberflächenschicht, die sich mit der Atmosphäre im Gleichgewicht befindet, von 550 m, die nur sehr schwach gekoppelt ist mit einer Tiefsee-Schicht mit einer Dicke von lediglich 190 m. Sie enthält nur 9% der Gleichgewichts-Reaktion, die dem Exponential-Term mit einer Zeitkonstante nach Jahrhunderten zuzuordnen ist. Diese Werte sind weder physikalisch realistisch hinsichtlich tatsächlicher Ozean-Charakteristika, noch sind sie kompatibel mit der Bandbreite von Werten, die von 2-Schichten-Modelen impliziert werden, die gut zu den Reaktionen der CMIP5 AOGCMs passen. Die anomalen Charakteristika des 2-Schichten-Modells von DICE2013Ra verursachen, dass dessen SCC und eine optimale Kohlenstoff-Steuer nur ein Drittel oder halb zu hoch sind während der ersten 100 Projektionsjahre. Dies hängt davon ab, welches der beiden physikalisch plausibleren alternativen 2-Schichten-Modellvarianten man betrachtet, die beide die gleichen ECS- und TCR-Werte haben wie DICE-2013Ra. Danach konvergiert die Kohlenstoff-Steuer rapide zum gleichen Wert, der in allen Fällen mit der Zeit abnimmt.
Qualitativ ähnliche vergleichbare Ergebnisse erhält man, falls der Parameter des DICE-2013Ra-Klimamoduls im Manual (c1) adjustiert wird, um ein TCR von 1,70°C zu erreichen, also den Wert, den man ursprünglich haben wollte, deren Parameter ebenfalls adjustiert werden, um jenen TCR für die beiden anderen 2-Schichten-Klimamodellvarianten zu erhalten. Das optimale Kohlenstoff-Steuer-Profil ist höher, und das Profil der resultierenden CO2-Emissionen niedriger, in allen drei Fällen. Die Tiefe der Ozean-Oberflächenschicht in DICE-2013Ra ist ein wenig flacher mit 476 m als mit den vorgegebenen Parameterwerten – immer noch viele Male höher als physikalisch realistisch oder innerhalb der Bandbreite von Werten, die erforderlich sind, um zum Verhalten der CMIP5-Klimamodelle zu passen. Das Verhältnis der Gleichgewichts-Reaktion, die dem Exponentialterm zugeordnet werden kann mit einer Zeitkonstante von einem Jahrhundert in DICE-2013Ra ist fast unbeeinflusst von der TCR-Änderung; es verharrt unrealistisch niedrig bei 9%.
Nun könnte man fragen, warum die optimale Kohlenstoff-Steuer höher und folglich das Niveau der Emissionen niedriger ist, wenn die weit überwiegende GMST-Reaktion aus dem box 1 exponential term resultiert, mit einer Zeitkonstante von vielen Jahrzehnten, anstatt gleichmäßiger verteilt zu sein zwischen den beiden Exponentialtermen mit Zeitkonstanten jeweils deutlich unter einem Jahrzehnt bzw. über einem Jahrhundert. Der Hauptgrund ist, dass im ersten Falle der von Emissionen verursachte zunehmende Antrieb, der um das Jahr 2090 nach dem Kohlenstoff-Steuer-Profil von DICE-2013Ra einen Spitzenwert erreicht, eine viel stärkere Zunahme der GMST im zweiten und dritten Jahrhundert verursacht als im zweiten Fall. Außerdem, fast die gesamte substantielle Erwärmung bis 2010 von 0,83°C [xxxiii] kommt im Projektionszeitraum des ersten Falles auf, während im zweiten Falle ein substantieller Anteil davon nach 300 Jahren unerkannt bleibt [xxxiv].
Für einen rationalen Ökonom oder Politiker könnte das zu erwartende relevante Ziel der gegenwärtige Wert (PV) des Gesamt-Nutzens sein, ermäßigt über den Zeithorizont von 300 Jahren – also genau das Ziel, das die optimale Kohlenstoff-Steuer maximiert. Im Basisfall berechnet DICE2013Ra den PV des Nutzens mit 2.678,6 (alle Angaben in Billionen Dollar des Jahres 2000). Mit der optimalen Kohlenstoff-Steuer und seinem eigenen Klimamodell erhöht sich der PV des Nutzwertes auf 2.707,0. Falls man die 2-Schichten-Modellvariante nach Boucher & Reddy heranzieht, steigt der PV des Nutzwertes noch weiter auf 2.722,8, nach Berntsen & Fuglestvedt auf 2.726,0 oder 19 Billionen Dollar über dem Niveau, welches sich nach dem DICE-2013Ra-2-Schichten-Klimamodell ergibt.Von größerer praktischer Bedeutung ist der Verlust an Nutzen, falls die höhere Kohlenstoff-Steuer, die optimal ist nach den Standard-Einstellungen im Klimamodul von DICE, eingeführt wird, wenn die tatsächliche Reaktion auf einer Linie liegt mit einem realistischeren 2-Schichten-Modell. Für die Variante nach Berntsen & Fuglestvedt beträgt dieser Verlust 1,1 Billionen Dollar, nach Boucher & Reddy 0,7 Billionen Dollar [xxxv]. Ein Verlust von 1 Billion Dollar des gegenwärtigen Nutzwertes macht etwa ein Dreißigstel des Gesamtnutzens aus, der dem Weltverbrauch des Einzeljahres 2010 zugeordnet werden kann.
Die Profile der Klimareaktionen in FUND und PAGE, also den beiden anderen, von der US-Regierung genutzten IAMs zur Abschätzung von SCC scheinen ebenfalls ungeeignet. Sie verwenden beide einen Exponential-Term mit einer einzigen Zeitkonstante in der Größenordnung von 40 Jahren. Daher hat kein Anteil an der Temperatur-Reaktion einen Jahrhundert-Zeitmaßstab (verglichen mit 9% in DICE-2013Ra). Daher scheint es wahrscheinlich, dass sie die optimale Kohlenstoff-Steuer bei jedwedem gegebenen Niveau von ECS und TCR überschätzen. Allerdings muss dieser Befund noch durch eine detaillierte Untersuchung bestätigt werden.
Es scheint ziemlich überraschend, dass alle drei hauptsächlichen IAMs Funktionen der Klimareaktion aufweisen mit ungeeigneten und physikalisch unrealistischen Zeitprofilen. In jedem Falle ist es Besorgnis erregend, dass Regierungen sowie ihre wissenschaftlichen und ökonomischen Berater diese IAMs herangezogen und offensichtlich nicht nachgeprüft haben, ob die Zeitprofile der resultierenden Klimareaktion vernünftig waren.
Übersetzt von Chris Frey EIKE
[Die folgenden Fußnoten werden nicht übersetzt, weil sie lediglich eine Fülle von Zusammenstellungen und Bezeichnungen enthalten. Anm. d. Übers.]
[i] See, e.g., https://www3.epa.gov/climatechange/EPAactivities/economics/scc.html.
[ii] Technical Support Document: Technical Update of the Social Cost of Carbon for Regulatory Impact Analysis Under Executive Order 12866 Interagency Working Group on Social Cost of Carbon, United States Government
[iii] Nordhaus, W. Integrated Economic and Climate Modelling. In Dixon, P.B., Jorgenson, D.W. (Eds.) Handbook of Computable General Equilibrium Modeling. Elsevier (2013) aida.wss.yale.edu/~nordhaus/homepage/documents/Nordhaus_IntegratedAssessmentModels_Handbook_2013.pdf
[iv] Anthoff D and RSJ Tol. The Climate Framework for Uncertainty, Negotiation and Distribution (FUND), Technical Description, Version 3.9 (2014) www.fund-model.org/Fund-3-9-Scientific-Documentation.pdf
[v] Hope, C. The PAGE09 integrated assessment model: A technical description. Cambridge Judge Business School Working Papers 4/2011, University of Cambridge (2011) https://www.jbs.cam.ac.uk/fileadmin/user_upload/research/workingpapers/wp1104.pdf
[vi] http://aida.wss.yale.edu/~nordhaus/homepage/
[vii] DICE-2013 model, beta version of April 22, 2013, developed by William Nordhaus, Yale University. aida.wss.yale.edu/~nordhaus/homepage/documents/DICE_2013R_112513m.xlsm
[viii] The new parameter values are given on page 96–97 of the Second edition( 31 October 2013) of the DICE-2013R manual, available at: aida.wss.yale.edu/~nordhaus/homepage/documents/DICE_Manual_103113r2.pdf . The reduction in the default ECS is discussed on page 18 of the manual.
[ix] Climate module parameter c1 has been changed from 0.104 to (at the default ECS of 2.9°C) 0.098, and c3 from 0.155 to 0.088. I have also incorporated the following other changes per the DICE-2013Rv2 GAMS code in the manual: in Initial atmospheric temperature in 2010, from 0.83°C to 0.80°C; Initial carbon emissions from land use, from 1.53972 to 3.3 GTCO2/yr; in Initial atmospheric concentration of CO2 (used for 2010), from 384.50 to 389.86; in Initial output, from 66.95 to 63.69 2005 $ trillion; in Industrial CO2 emissions for 2010, from 8930 to 9168 MTC; in forcings of non- CO2 GHGs from −0.06 in 2000 and −0.62 in 2100 to 0.25 in 2010 and 0.75 in 2100 (Wm-2); and in the Damage coefficient on temperature squared, from 0.002131 to 0.00267. Minor other differences in the abatement module have been left untouched, as has the growth of population , which differs only marginally between the Excel and GAMS versions.
[x] Parameter c1, also termed ξ1 in the manual and there wrongly referred to as the diffusion parameter and overstated there by a factor of ten.
[xi] Nordhaus, W. Integrated Economic and Climate Modelling, op. cit., p.1088.
[xii] Gregory JM, Vertical heat transports in the ocean and their effect on time-dependent climate change. Clim Dyn (2000) 16:501±515.
[xiii] Held, I. M. et al, Probing the fast and slow components of global warming by returning abruptly to preindustrial forcing. J. Climate, 23 (2010), 2418–2427.
[xiv] The heat capacity of the atmosphere and land is small relative to that of the ocean mixed layer, and is subsumed within the value used for it.
[xv] Berntsen, T and J Fuglestvedt. Global temperature responses to current emissions from the transport sectors. PNAS 105 (2008), 19154–19159. See the Supplementary Information.
[xvi] The annual maximum depth of the ocean surface mixed layer is relevant here.
[xvii] It might be thought that a 1D model in which heat is transferred diffusively between a surface mixed layer and thermocline/ deep ocean, with slow upwelling linked to sinking cold water in polar regions often also being included, would be more appropriate. However, as much of the heat is believed to be transported between ocean layers by advection of water along sloping isopycnal surfaces (Gregory 2000, op. cit.) the simpler 2-box model treatment appears to be satisfactory.
[xviii] Caldeira K and N P Myhrvold. Projections of the pace of warming following an abrupt increase in atmospheric carbon dioxide concentration. Environ. Res. Lett. 8 (2013) 034039 (10pp)
[xix] Ricke K and Caldeira D. Maximum warming occurs about one decade after a carbon dioxide emission Environ Res Lett 9 (2014) 124002 doi:10.1088/1748-9326/9/12/124002
[xx] Geoffrey et al (2013) carried out a similar exercise with a different, overlapping set of CMIP5 models and found good fits, with the values of τ1 and τ2 giving the best fit varied in the ranges 1.6 – 5.5 and 126 – 698 years respectively. Geoffroy O et al. Transient Climate Response in a Two-Layer Energy-Balance Model. Part I: Analytical Solution and Parameter Calibration Using CMIP5 AOGCM Experiments J. Clim. 26 (2012) 1841–57
[xxi] Based on the HadCM3 forcing for a doubling of CO2 concentration of 3.68 Wm-2.
[xxii] The Global Temperature change Potentials given in Table 8.A.1 of AR5.
[xxiii] For the ocean only, based on the ocean covering 71% of the Earth’s surface and a seawater volumetric heat capacity of 4.1 M J K-1 m-3.
[xxiv] Moreover, the theoretical TCR I calculate using the two-box model parameters is only 1.51°C. The difference appears to be due to use of a 5-year time step and to applying forcing increments at the start of each period. When a 1-year time step is used, the TCR calculated from applying a 70-year forcing ramp is only 0.01°C above the theoretical value.
[xxv] If the surface ocean depth in the Boucher & Reddy based variant is swapped with that in the Berntsen & Fuglestvedt based one and the FSD values altered to maintain their TCRs, the shapes of the resulting response curves are almost bounded between those for the two versions with unswapped surface ocean depths over the entire 250-year period.
[xxvi] The warming in the second term of the two exponential representation of a 2-box model is not the same as that of the deep ocean layer in the underlying physical model, which ultimately warms as much as the surface.
[xxvii] In DICE-2013R, the forcing from a doubling of atmospheric CO2 concentration is 3.8 Wm-2, so the sum of the sensitivity factors for each model variant is 2.9/3.8 = 0.763
[xxviii] The carbon tax model specifies an initial value, initial growth rate, and a rate of change of growth rate that increases by the same specified amount each year. Fixed reductions are applied in the final three periods, matching those in the downloaded Excel model (the reasons for which are unknown); doing so has a negligible effect on the present value of utility. When all parameter values are as in the downloaded model, optimising the four parameter fit produces an almost identical carbon tax profile to that in the downloaded model, which were derived by optimising each period’s carbon tax independently, and the present value of utility is unchanged to seven significant figures.
[xxix] Per the DICE manual, the backstop technology can replace all fossil fuels; it could be one that removes carbon from the atmosphere or an all-purpose environmentally benign zero-carbon energy technology. The downward trend in its price is based on assumed technological progress.
[xxx] Up to 2290, from when on the fixed reductions referred to in note 28 are applied.
[xxxi] More precisely, 68% for Berntsen & Fuglestvedt and 73–76% for Boucher & Reddy.
[xxxii] Land use change emissions, which in DICE20113R are assumed to decline on a fixed basis, are not included. In the base case the $1 initial carbon tax increases by 10.4% in each pentad until 2015, from when the backstop CO2 price is applied.
[xxxiii]The currently unrealised, “in-the-pipeline”, warming at the end of 2010 equals ECS of 2.9°C x Forcing in 2010 of 2.14 Wm-2 / Forcing for a doubling of CO2 of 3.8 Wm-2, minus Atmospheric temperature rise in 2010 above preindustrial of 0.8°C.
[xxxiv] 0.80°C of the 0.83°C unrealised warming as at 2010 emerges by the end of the projections when the DICE-2013Ra climate module parameters are used, but only 0.45°C or 0.60°C when parameters based respectively on the Berntsen & Fuglestvedt or Boucher & Reddy models are used.
[xxxv] In the contrary cases, where the actual climate response is as per the DICE-2013Ra 2-box model but a lower carbon tax that is optimum for one of the two variants is imposed, the utility losses are a little (10-20%) larger. However, it is most unlikely that the DICE-2013Ra response could be realistic.
A PDF version of this article is available [here].