Noch einmal: Precipitable Water*
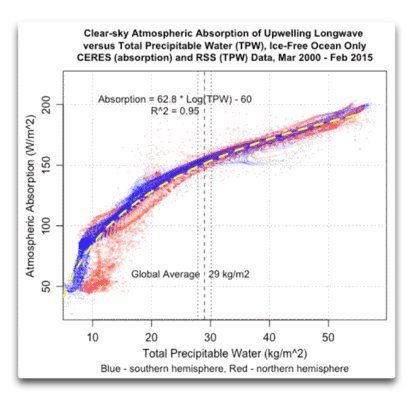
Abbildung 1: Scatterplot mit TPW (X-Achse) im Verhältnis zu Atmosphärischer Absorption (Y-Achse). Die gestrichelte vertikale Linie zeigt den nach Gebiet gewichteten globalen mittleren Wert. Gepunktete vertikale Linien zeigen die Bandbreite des globalen Mittelwertes über den Zeitraum. Die Neigung der Kurve an jedem Punkt beträgt 62,8/TPW (W/m² pro Grad)
In diesem Beitrag betrachte ich die andere Hälfte der Beziehung. Diese ist die Beziehung zwischen der Wassertemperatur der Ozeane an deren Oberfläche und das gesamte precipitable water. Die gute Nachricht lautet, dass wir anders als bei den CERES-Daten, die nur 15 Jahre zurück reichen, TPW-Aufzeichnungen seit dem Jahr 1988 haben, ebenso wie Wassertemperaturen für den gleichen Zeitraum. Abbildung 2 zeigt die Beziehung zwischen diesen beiden Größen:
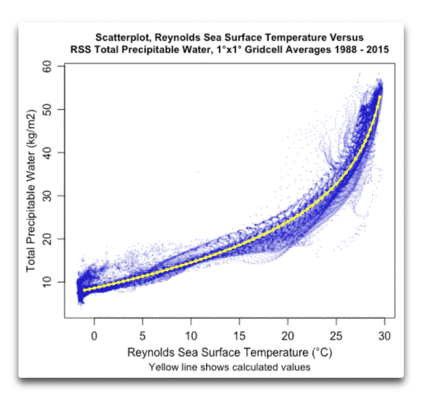
Abbildung 2: Scatterplot, TPW-Daten von RSS im Verhältnis zu ReynoldsOI-Wassertemperaturen. Siehe Anmerkungen am Ende zu den Datenquellen.
Wie man sieht, ist die Beziehung geordnet, aber nicht einfach. Zuerst dachte ich, dass die Beziehung logarithmisch sei, aber es zeigte sich, dass dem nicht so ist. Auch eine Potenzfunktion [power function] repräsentiert das Verhältnis nur sehr schlecht. Nachdem ich erfolglos eine Vielfalt von Kurven untersucht hatte, kam ich zu dem Ergebnis, dass man sich dem Ganzen mit einer inversen S-förmigen Kurve [sigmoid function] nähern könnte (oben in gelb dargestellt). Angesichts der sehr smarten Leute hier denke ich, dass irgendjemand in der Lage sein wird, eine physikalische Begründung zusammen mit der richtigen Gleichung zu liefern. Aber für das, was ich hier darlegen möchte, reicht es.
Nun, die Beziehung zwischen Wasserdampf und atmosphärischer Absorption ist eindeutig logarithmisch, wie es von der Theorie auch vorgegeben wird. Andererseits kenne ich keinerlei einfache Theorien zur Beziehung zwischen Wassertemperatur und Gesamt-PW. Zum Beispiel passt die Kurve nicht zur Clausius-Clapeyron’schen Zunahme des Wasserdampfes. Und eindeutig ist mein Verfahren rein heuristisch und brute-force … aber das ist in Ordnung, weil ich nicht behaupte, dass es erläuternd ist. Ich verfolge einen anderen Zweck. Ich will nämlich herausfinden, wie stark sich das PW pro Grad Änderung der Wassertemperatur ändert. Und für diesen Zweck muss die Funktion ableitbar sein.
Zunächst einmal möchte ich erklären, wo wir stehen. Im vorigen Beitrag habe ich eine mathematische Beziehung abgeleitet zwischen den beiden in Abbildung 1 gezeigten Variablen. Dabei handelt es sich um die atmosphärische Absorption der ausgehenden langwelligen Strahlung bei klarem Himmel von der Erdoberfäche sowie der Gesamt-PW-Gehalt (TPW) der Atmosphäre.
Und zu Beginn dieses Beitrags habe ich eine mathematische Beziehung zwischen den beiden in Abbildung 2 gezeigten Variablen hergeleitet. Das sind der Gesamt-PW-Gehalt der Atmosphäre und die Wassertemperatur SST.
Das bedeutet: setzt man Letzteres in Ersteres ein, kann ich eine mathematische Beziehung herleiten zwischen der SST und der atmosphärischen Absorption.
Natürlich wollte ich meine Formel grundlegend testen, welche die Wassertemperatur mit der atmosphärischen Absorption verbindet. Ich habe bzgl. der Absorption nur die CERES-Daten, so dass hier ein kürzerer Zeitraum abgedeckt ist als in Abbildung 2. Da die Gesamt-Beziehung mit den Reynolds-Wassertemperaturdaten erstellt worden ist, habe ich diese für den Vergleich herangezogen.
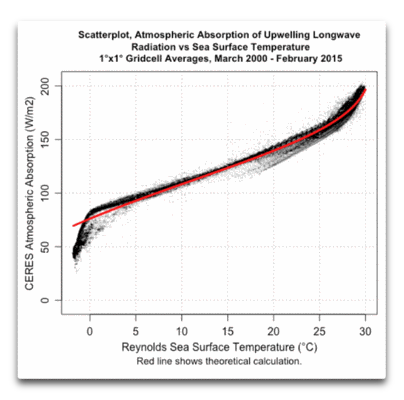
Abbildung 3: Atmosphärische Absorption langwelliger Strahlung im Verhältnis zur Wassertemperatur. Zur mathematischen Herleitung siehe die Anmerkungen am Ende.
Ich bin recht zufrieden damit als Vergleich zwischen theoretischer und gemessener atmosphärischen Absorption. Dazu ein paar Bemerkungen. Erstens, die Differenz unter 0°C kommt zustande, weil CERES und Reynolds bei Frost Dinge messen, die sich geringfügig unterscheiden, sobald Eis ins Spiel kommt. CERES misst die mittlere Temperatur des Eises und des Wassers, während Reynolds allein die Wassertemperatur erfasst.
Weiter. Die leichte Krümmung der schwarzen Linie von 0°C bis 25°C folgt nicht vollständig der roten Linie. Ursache hierfür ist, dass ich die Daten unter dem Gefrierpunkt mit einbezogen habe, was die Ergebnisse etwas verzerrt hat. Vielleicht hätte ich diese Daten außen vor lassen sollen, aber ich dachte, der Vollständigkeit halber…
Die leichte Krümmung der schwarzen Linie von 0°C bis 25°C ist der Tatsache geschuldet, dass die Strahlung der Oberfläche proportional zur vierten Potenz der Temperatur ist. Falls man die Absorption berechnet hätte gegen die ausgehende Strahlung anstatt gegen die Temperatur, hätte sich eine gerade Linie ergeben. Ich habe es so gemacht, weil es viele Diskussionen um den Wert der „Wasserdampf-Strahlungs-Rückkopplung“ [water vapor radiative feedback] gibt, die pro Grad Celsius gemessen wird. Ich könnte eine bessere Näherung erhalten, wenn ich die T↑4-Beziehung einbezogen hätte, aber meine Schlussfolgerung war, dass das Ergebnis nicht den Aufwand gerechtfertigt hätte … falls ich eine größere Genauigkeit benötige, kann ich die Abbildung noch einmal errechnen, aber für jetzt ist sie mehr als ausreichend.
Die Stärke der Rückkopplung wird berechnet als die Neigung der roten Linie in Abbildung 3. Die Neigung ist die Änderung der Absorption für eine Änderung um 1°C der Wassertemperatur. Abbildung 4 zeigt die Amplitude der Wasserdampf-Strahlungs-Rückkopplung über die Bandbreite der ozeanischen Wassertemperaturen:
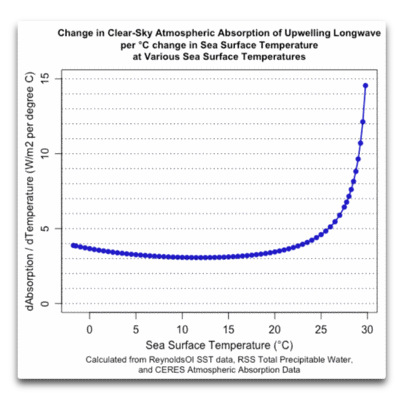
Abbildung 4: Wasserdampf-Strahlungs-Rückkopplung, berechnet als die Änderung der atmosphärischen Absorption ausgehender langwelliger Strahlung pro 1°C Änderung der Wassertemperatur.
Das ist ein sehr interessanter Verlauf. Angesichts der allgemeinen Form der Abbildungen 1 und 2 hätte ich dieses Aussehen erwarten können … aber es kam irgendwie als Überraschung. In den meisten Gebieten der Welt heben sich die beiden Tendenzen gegenseitig auf, und die Wasserdampf-Strahlungs-Rückkopplung bei klarem Himmel beträgt etwa 3 bis 4 W/m² pro Grad Celsius. Aber in den Tropen, wo das Wasser warm ist, schießt die Wasserdampf-Rückkopplung in den Himmel.
Diskussion
Mit einer so großen Strahlungs-Rückkopplung von Wasserdampf, drei bis vier Watt pro Quadratmeter pro Grad und noch viel höher in den Tropen – warum gibt es da keine Runaway-Rückkopplung? Ich meine: die so genannte, vom IPCC behauptete „Klima-Sensitivität“ lautet, dass 2 bis 3 W/m² zusätzliche Strahlung zu einem Grad Erwärmung führt. Und den Beobachtungen oben zufolge, wenn es sich um ein Grad erwärmt, bekommen wir eine zusätzliche einfallende Strahlung durch Wasserdampf von 3 bis 4 W/m². Und von dieser Menge wird behauptet, dass sie ausreichend sei für mehr als ein Grad zusätzliche Erwärmung … ein Garant für eine positive Runaway-Rückkopplung, falls ich jemals eine gesehen habe. Also – mit jener hohen Strahlungs-Rückkopplung, warum zeigt sich keine Runaway-Rückkopplung?
Man könnte beginnen mit der sorgfältigen Lektüre der Diskussion von Dr. Roy Spencer zu diesem Thema, nämlich Five Reasons Why Water Vapor Feedback Might Not Be Positive. Die TL-DR-Version lautet: wenn der Wasserdampf-Gehalt in der Luft zunimmt, nimmt die einfallende Strahlung tatsächlich zu … aber es gibt auch noch viele andere Dinge, die sich ebenfalls ändern.
Als ein von Dr. Spencer erwähntes Beispiel in seiner Diskussion des Verhältnisses zwischen Wasserdampf und Niederschlagsmenge sagte er:
Während wir wissen, dass die Verdunstung mit der Temperatur zunimmt, wissen wir nicht sehr viel darüber, wie sich die Effizienz von Niederschlags-Systemen mit der Temperatur ändert.
Letzterer Prozess ist viel komplexer als die Verdunstung von der Erdoberfläche (Renno et al. 1994), und es ist keineswegs geklärt, ob sich Klimamodelle diesbezüglich realistisch verhalten.
Da möchte ich noch etwas hinzufügen. Die Regenmenge steigt mit steigendem atmosphärischen Wassergehalt, wie Abbildung 5 zeigt:
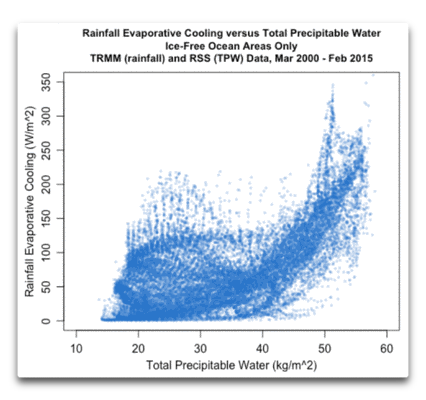
Abbildung 5: Scatterplot, Verdunstungskühlung durch Regen im Verhältnis zu TPW. Die TRMM-Daten überdecken lediglich die Breiten zwischen 40°N und 40°S.
Man beachte die Größenordnung der involvierten Abkühlung … nicht Watt pro Quadratmeter, sondern hunderte Watt pro Quadratmeter. Während PW von etwa 40 bis 55 kg pro Quadratmeter reicht, reicht die Verdunstungsabkühlung von 50 bis 250 Watt pro Quadratmeter oder mehr … das ist eine große Abkühlung, etwa zehn Watt pro zusätzlicher Abkühlung pro zusätzlichem kg von PW.
Das können wir vergleichen mit der Neigung der zunehmenden Wasserdampf-Strahlungs-Rückkopplung in Abbildung 1. Die Neigung in Abbildung 1 beträgt 62,8 W/m² dividiert durch TPW, so dass sich bei einem TPW von 50 kg/m² etwa 1,2 W/m² zusätzliche Strahlungs-Erwärmung pro zusätzlichem kg/m² Wasser ergeben würde … gegen 10 W/m² Verdunstungs-Abkühlung durch Regen pro zusätzlichem kg/m² Wasser.
Aber Moment … da ist noch mehr. Abbildung 6 zeigt die Verdunstungsabkühlung durch Regen im Vergleich zur Wassertemperatur SST. Da SST und PW in einer engen Beziehung zueinander stehen, sieht Abbildung 6 der Abbildung 5 ziemlich ähnlich:
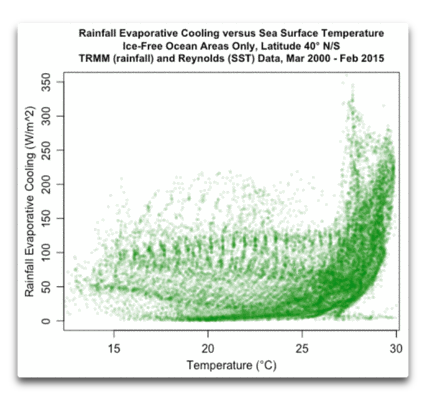
Abbildung 6: Scatterplot, Verdunstungsabkühlung durch Regen im Vergleich zu Reynolds-Wassertemperaturen SST.
Wie in Abbildung 5 steigt die Verdunstungsabkühlung durch Regen am warmen (rechten) Ende der Skala von 50 bis etwa 200 W/m² sehr schnell. Allerdings ist es hier von Bedeutung, dass die SST von 27°C bis 30°C reicht. Und das ergibt eine Gesamt-Abkühlung von etwa 50 W/m² pro Grad … was die 3 bis 4 W/m² wasserdampf-basierter Erwärmung des IPCC ziemlich marginalisiert …
Es gibt einen weiteren interessanten Aspekt bei Abbildung 6, und zwar die leere Fläche unten rechts. Ich habe immer gesagt, dass thermoregulierende Phänomene wie Gewitter von Temperaturschwellen abhängen. Die leere Fläche in der unteren rechten Ecke von Abbildung 7 zeigt, dass oberhalb einer bestimmten Wassertemperatur … der Regen diese abkühlt. Und nicht nur der Regen, sondern auch je wärmer es wird, desto größer die Gesamt-Verdunstungs-Abkühlung und desto größer auch die minimale Verdunstungs-Abkühlung.
Die Abkühlungseffekte von Wasserdampf hören hier aber noch nicht auf. Zunehmender Wasserdampf lässt auch die Größe der absorbierten Sonnenenergie zunehmen, wenn sie durch die Atmosphäre dringt. Wie bei der Absorption der ausgehenden langwelligen Strahlung ist die Beziehung auch hier logarithmisch. Abbildung 7 zeigt diese Beziehung:
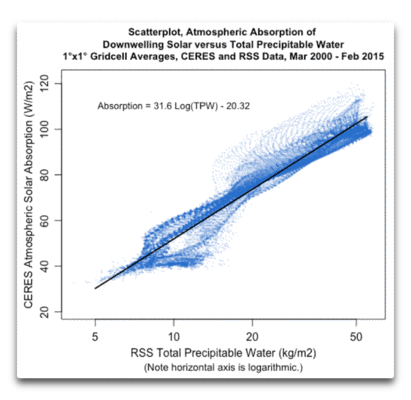
Abbildung 7: Scatterplot, atmosphärische Absorption der einfallenden Solarstrahlung (Y-Achse) im Verhältnis zu TPW (X-Achse).
Logarithmische Beziehungen der Form „m log(x) + b” haben eine einfache Neigung, nämlich m/x. Die Neigung der Gleichung in Abbildung 7 beträgt 31,6/TPW (W/m² pro Grad). Zuvor haben wir gesehen, dass die Neigung der Erwärmung durch zunehmenden Wassergehalt 62,8/TPW (W/m² pro Grad) betragen hatte. Dies bedeutet, dass zu jedem Punkt die Hälfte der Erwärmung durch Wasserdampf-Strahlungs-Rückkopplung kompensiert wird durch den Verlust der einfallenden Sonnenstrahlung infolge zusätzlichen Wasserdampfes.
Und auch das ist noch nicht das Ende der damit zusammenhängenden Phänomene … Abbildung 8 zeigt die Korrelation zwischen TPW und Wolken-Albedo:
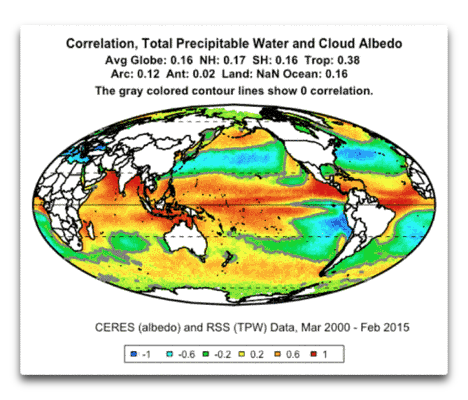
Abbildung 8: Korrelation von TPW und Wolken-Albedo
Wie man sieht, wenn in den Tropen PW zunimmt, nimmt auch die Wolken-Albedo zu (rot-gelb). Das macht Sinn: mehr Wasser in der Luft bedeutet mehr Bewölkung. Auch dies hat einen Abkühlungseffekt zur Folge.
Dies ist auch keine vollständige Liste. Nicht angesprochen habe ich Änderungen der einfallenden langwelligen Strahlung durch Wolken … immer neue Beziehungen.
Schlussgedanken
Das Zentrum der Klimaaktivitäten liegt in den Tropen. Die Hälfte des verfügbaren Sonnenlichtes trifft auf die Erde zwischen 23°N und 23°S. Die wesentlichen Phänomene, die die einfallende Solarstrahlung regulieren, treten in den Tropen auf. Und wie die Graphen oben zeigen, befindet sich die Menge des Wassers in der Atmosphäre im Herzen jener Phänomene.
Ist also die Rückkopplung von Wasserdampf positiv oder negativ? Alles in allem muss ich sagen, dass sie deutlich negativ ist, aus zwei Gründen. Der erste Grund ist die langzeitliche Stabilität des globalen Klimasystems (z. B. betrug die Änderung der globalen Temperatur nur ± 0.3°C während des gesamten 20. Jahrhunderts). Dies impliziert eher eine negative anstatt einer positiven Rückkopplung.
Der zweite Grund sind die relativen Größenordnungen der oben beschriebenen verschiedenen Rückkopplungen. Diese werden dominiert durch Verdunstungsabkühlung infolge Regens und durch die Änderungen des reflektierten Sonnenlichtes infolge der Albedo. Beides ist viel größer als die 3 bis 4 W/m² der von Wasserdampf induzierten Strahlungs-Erwärmung.
Allerdings gibt es eine sehr große Schwierigkeit, wenn man die so genannte „Wasserdampf-Rückkopplung“ von der Myriade anderer Phänomene isolieren will. Diese Schwierigkeit ist eingebettet in etwas, das ich den „Ersten Hauptsatz des Klimas“ nenne, der da lautet:
Im Klimasystem hängt alles mit allem zusammen … was wiederum mit allem zusammenhängt … außer wenn das nicht der Fall ist.
Beispiel: Die Temperatur beeinflusst den [Gehalt von] Wasserdampf – steigt die Temperatur, steigt auch der Wasserdampfgehalt. Steigt der Wasserdampfgehalt, nehmen auch Bewölkung und Regenmenge zu. Wenn Bewölkung und Regenmenge zunehmen, sinken die Temperaturen. Wenn die Temperatur sinkt, verringert sich der Wasserdampf … man erkennt hier das Problem. Anstatt Dinge zu haben, die eindeutig Ursache bzw. eindeutig Folge sind, besteht das gesamte System aus etwas, das ich eine „Zirkelkette von Effekten“ nenne, in der es keine eindeutige Ursache und keine eindeutigen Begrenzungen gibt.
Wie auch immer, das sind die Einsichten, die sich mir mit der Untersuchung des PW-Datensatzes erschlossen haben.
Da ich gerade von ;precipitable water‘ spreche – hier geht gerade die Sonne unter. Wenn ich aus dem Küchenfenster auf den Ozean schaue, sehe ich den vom Pazifik herein treibenden Nebel. Er wabert in Wellen über die fernen Hügel, verschluckt die Bäume auf dem Weg zu unserem Haus … gestern Abend gab es das gleiche Schauspiel.
(Siehe Bild oben rechts).
Ich liebe diesen Seenebel. Er riecht nach meinem geliebten Ozean; trägt den Geruch von Fischerbooten und Muscheln, von versteckten Höhlen und Jugendträumen. Und wenn der Nebel herein treibt, bringt er den Klang des Nebelhorns am Ende der Bodega Bay mit sich. Es sind etwa zehn Kilometer von meinem Haus zu dieser Bucht, aber der Klang scheint in der Nebelschicht gefangen. Dann pausiere ich mit meiner wissenschaftlichen Arbeit – und genieße einfach den Augenblick.
————————————–
Anmerkungen [nicht übersetzt]:
The math … I start with the equation for relationship between absorption (A) and total precipitable water (TPW) shown in Figure 1:
A = 62.8 Log(TPW) – 60
To this I add the inverse sinusoidal relationship between TPW and sea surface temperature, as shown in Figure 2:
TPW = – 13.5 Log[-1 + 1/(0.00368 SST + .887)] -19.1
Combining the two gives us:
A = 62.8 Log[-19.1 – 13.5 Log[-1 + 1/(0.887 + 0.00368 SST)]] – 60
Differentiating with respect to sea surface temperature gives the result as shown in Figure 3:
dA/dT = 3.13/((-1 + 1/(0.887 + 0.00368 SST)) (0.887 + 0.00368 SST)^2 (-19.1 – 13.5 Log[-1 + 1/(0.887 + 0.00368 SST)]))
Further Reading: NASA says water vapor feedback is only 1.1 W/m2 per degree C …
DATA
Reynolds SST data, NetCDF file at the bottom of the page
TRMM data, NetCDF file at the bottom of the page
Link: https://wattsupwiththat.com/2016/07/28/precipitable-water-redux/
Übersetzt von Chris Frey EIKE