Es war eine sehr interessante Konferenz, und als Nebenaspekt nahm ich mit nach Hause, dass der kurzfristige Notfall die islamistische Gewalt ist und der langfristige Notfall, dass irgendwelche Riesen-Meteore auf die Erde stürzen. Aber bitte, gleiten Sie bei der Diskussion zu diesem Vortrag nicht in diese beiden Themen ab.

Abstract: Ursprünglich war das Abstract länger, aber hier folgt die Kurzform. Jene, die die globalen gemittelten Lufttemperaturen zusammenstellen, haben nicht nur systematische Messfehler (siehe auch hier) ignoriert, sondern haben sogar auch die Messgenauigkeit der Instrumente selbst in Abrede gestellt. Seit mindestens dem Jahr 1860 wurde die Thermometer-Genauigkeit nur vage berücksichtigt. Ebenfalls seit jenem Jahr sowie im 95%-Vertrauens-Intervall ist die Rate oder Größenordnung des globalen Anstiegs der Lufttemperatur nicht erkennbar. Gegenwärtiger Streit über die Lufttemperatur und seiner Beispiellosigkeit ist spekulative Theologie.

1. Einführung: Systematischer Fehler

Systematische Fehler treten bei experimentell oder anders gemessenen Ergebnissen auf durch unkontrollierte und oftmals kryptische deterministische Prozesse (1). Diese können so einfach sein wie ein konsistenter Fehler des Bedieners. Typischer jedoch entstehen Fehler aus einer unkontrollierten experimentellen Variable oder Ungenauigkeit der Instrumente. Ungenauigkeit der Instrumente resultiert aus einer Fehlfunktion oder dem Fehlen einer Kalibrierung. Unkontrollierte Variable können die Größenordnung einer Messung beeinflussen und/oder den Verlauf eines Experimentes. Abbildung 1 zeigt die Auswirkung einer unkontrollierten Variable. Sie stammt aus meinen eigenen Arbeiten (2, 3):

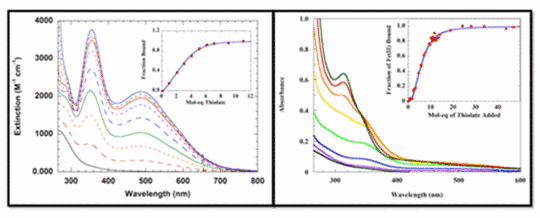
Abbildung 1: Links: Titration gelösten Eisens [ferrous iron] unter Bedingungen, die ungeplant eine Spur Luft in das Experiment gelangen lassen. Kleine Graphik darin: Die inkorrekten Daten folgen präzise der Gleichgewichts-Thermodynamik. Rechts: das gleiche Experiment, aber mit einer angemessen strikten Abwehr von Luft. Die Daten sind total unterschiedlich. Kleine Graphik rechts: die korrekten Daten zeigen eine ausgesprochen unterschiedliche Thermodynamik.

Abbildung 1 zeigt, dass der unbeabsichtigte Eintritt einer Spur Luft ausreichte, um den Verlauf des Experimentes vollkommen zu verändern. Nichtsdestotrotz zeigen die fehlerhaften Daten ein kohärentes Verhalten und folgen einer Trajektorie, die vollkommen konsistent ist mit der Gleichgewichts-Thermodynamik. In allen Erscheinungen war das Experiment gültig. Isoliert betrachtet sind die Daten überzeugend. Allerdings sind sie vollständig falsch, weil die eingetretene Luft das Eisen chemisch modifiziert hat.

Abbildung 1 zeigt exemplarisch die Gefahr eines systematischen Fehlers. Kontaminierte experimentell oder anders gemessene Ergebnisse können sich genau wie gute Daten verhalten und daherkommen sowie rigoros validen physikalischen Theorien folgen. Lässt man hier keine Vorsicht walten, laden solche Daten zu falschen Schlussfolgerungen ein.

Ein systematischer Fehler ist seiner Natur nach schwer zu erkennen und zu entfernen. Zu den Methoden der Entfernung gehören sorgfältige Kalibrierung der Instrumente unter Bedingungen, die mit der Messung oder dem Experiment identisch sind. Methodisch unabhängige Experimente, die das gleiche Phänomen behandeln, bieten eine Möglichkeit, die Ergebnisse zu prüfen. Sorgfältige Aufmerksamkeit bzgl. dieser Verfahren ist Standard in den experimentellen physikalischen Wissenschaften.

Die jüngste Entwicklung einer neuen und höchst genauen Atomuhr zeigt die extreme Vorsicht, die Physiker walten lassen, wenn sie systematische Fehler eliminieren wollen. Kritisch für die Erreichung einer Genauigkeit von 10^-18 Sekunden war die Ausmerzung eines systematischen Fehlers, den die Schwarzkörperstrahlung des Instrumentes selbst erzeugte (4).

Abbildung 2 [oben rechts]: Nahaufnahme der neuen Atomuhr. Das Zeitmess-Element ist ein Cluster fluoreszierender Strontium-Atome, eingehüllt in ein optisches Netz. Thermisches Rauschen wird entfernt mittels Daten eines Sensors, der die Schwarzkörper-Temperatur des Instrumentes misst.

Abschließend hierzu: Ein systematischer Fehler mittelt sich mit wiederholten Messungen nicht heraus. Die Wiederholung kann den Fehler sogar verstärken. Wenn systematische Fehler nicht eliminiert werden können, um deren Existenz man aber weiß, müssen Angaben zur Unsicherheit zusammen mit den Daten angezeigt werden. In graphischen Präsentationen gemessener oder gerechneter Daten wird der systematische Fehler durch Balken der Fehlerbandbreite repräsentiert (1). Jene Balken geben Aufschluss über die Zuverlässigkeit des Ergebnisses.

2. Systematische Fehler bei Temperaturmessungen

2.1 Lufttemperatur auf dem Festland

Während des größten Teils des 20. Jahrhunderts wurden die Temperaturen auf dem Festland mittels eines Thermometers gemessen, in dem sich eine Flüssigkeit hinter Glas befand. Es war eingebettet in eine Wetterhütte (5, 6). Nach etwa 1985 kamen Thermistoren oder Platin-Widerstands-Thermometer (PRT) zum Einsatz, die sich in einer unbelüfteten zylindrischen Plastikumhüllung befanden. Dies erfolgte in Europa, den Anglo-Pazifischen Ländern und den USA. Seit dem Jahr 2000 platzierte das Climate Research Network der USA Sensoren in einer belüfteten Umhüllung, die ein Trio von PRTs enthielten (5, 7, 8, 9). Eine belüftete Schutzhülle enthält einen kleinen Ventilator, der für einen Austausch der Luft im Inneren der Hülle mit der Außenluft sorgt.

Unbelüftete Sensoren stützen sich auf vorherrschenden Wind zur Ventilation. Sonnenstrahlung kann die Umhüllung des Sensors aufheizen, was die Innenluft um den Sensor erwärmt. Im Winter kann aufwärts gerichtete Strahlung durch die Albedo einer schneebedeckten Erdoberfläche ebenfalls einen Warm-Bias erzeugen (10). Zu bedeutenden systematischen Messfehlern kommt es, wenn die Windgeschwindigkeit unter 5 m/s liegt (9, 11).

Abbildung 3: Der Plaine Morte Glacier in der Schweiz. Hier wird gezeigt, wie das Experiment der Kalibrierung des Lufttemperatur-Sensors von Huwald et al. während der Jahre 2007 und 2008 durchgeführt worden ist (12). Eingebettet: Nahaufnahmen der PRT und Schall-Anemometer-Sensoren. Bild: Bou-Zeid, Martinet, Huwald, Couach, 2.2006 EPFL-ENAC.

Bei den während der Jahre 2007 und 2008 durchgeführten Kalibrierungs-Experimenten auf dem Gletscher (Abbildung 3) wurde die Feld-Genauigkeit des RM Young PRT innerhalb einer unbelüfteten Umhüllung über einer schneebedeckten Oberfläche getestet. Im Labor kann der RM Young Sensor mit einer Genauigkeit von ±0,1°C anzeigen. Die Genauigkeit auf dem Feld wurde bestimmt durch den Vergleich von Lufttemperaturen, gemessen mittels eines Schall-Anemometers, wobei der Effekt ausgenutzt wird, dass die Temperatur Einfluss auf die Schallgeschwindigkeit in der Luft hat. Dies ist unabhängig von Strahlung und Windgeschwindigkeit.

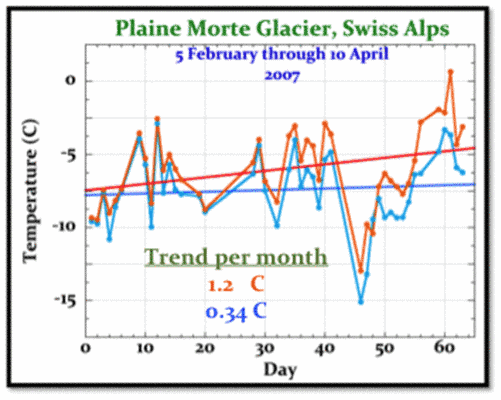
Abbildung 4: Gleichzeitig aufgezeichnete Temperaturtrends auf dem Plaine Morte-Gletscher von Februar bis April 2007. (¾), Sonic anemometer, and; (¾), RM Young PRT probe.

Abbildung 4 zeigt, dass bei identischen Umwelt-Bedingungen der RM Young-Sensor deutlich höhere winterliche Lufttemperaturen aufgezeichnet hat als das Schall-Anemometer. Die Neigung des RM Young-Temperaturtrends ist auch mehr als dreimal größer. Verglichen mit einem üblichen Mittel würde der Fehler von RM Young einen unechten Erwärmungstrend in ein globales Temperaturmittel einbringen. Die noch größere Bedeutung dieses Ergebnisses ist, dass RM Young im Design und der Reaktion sehr ähnlich ist den verbesserten Temperaturmessungen, die weltweit seit etwa 1985 verwendet werden.

Abbildung 5 zeigt ein Histogramm des systematischen Temperaturfehlers, der beim RM Young in Erscheinung tritt.

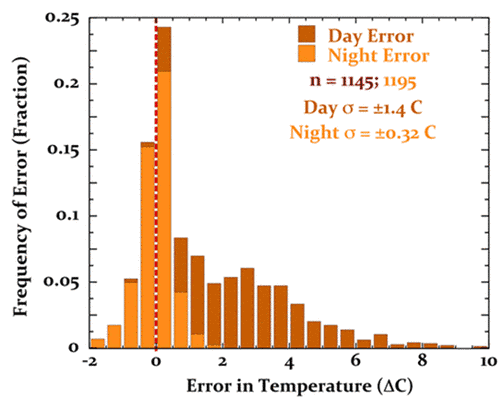
Abbildung 5: Systematischer Fehler von RM Young auf dem Plaine Morte-Gletscher. Der Fehler tagsüber beträgt 2.0°C ± 1.4°C, der Fehler nachts 0.03°C ± 0.32°C.

Die systematischen Fehler von RM Young bedeuten, dass im Falle des Fehlens eines unabhängigen Kalibrierungs-Instrumentes jedwede gegebene tägliche Mitteltemperatur eine damit verbundene Unsicherheit von 1°C ± 1.4°C aufweist [an 1s uncertainty]. Abbildung 5 zeigt, dass diese Unsicherheit weder zufällig verteilt noch konstant ist. Sie kann nicht entfernt werden durch Mittelung individueller Messungen oder wenn man Anomalien heranzieht. Die Subtraktion des mittleren Bias‘ wird nicht die normale 1s-Unsicherheit [?] entfernen. Fügt man die Temperaturaufzeichnung der RM Young-Station in ein globales Mittel ein, wird dies den mittleren Fehler mit hineintragen.

Vor der Inklusion in einem globalen Mittel werden Temperaturreihen individueller meteorologischer Stationen statistischen Tests der Datenqualität unterzogen (13). Von den Lufttemperaturen weiß man, dass sie eine Korrelation von R = 0,5 über Entfernungen von etwa 1200 km zeigen (14, 15). Der erste Test der Qualitätskontrolle jeder gegebenen Stationsaufzeichnung enthält einen statistischen Check der Korrelation mit Temperaturreihen benachbarter Stationen. Abbildung 6 zeigt, dass eine mit dem RM Young-Fehler kontaminierte Temperaturreihe diesen grundlegendsten aller Tests bestehen wird. Außerdem wird die irrige RM Young-Aufzeichnung jeden einzelnen statistischen Test bestehen, der bzgl. der Qualitätskontrolle von Aufzeichnungen meteorologischer Stationen weltweit durchgeführt wird.

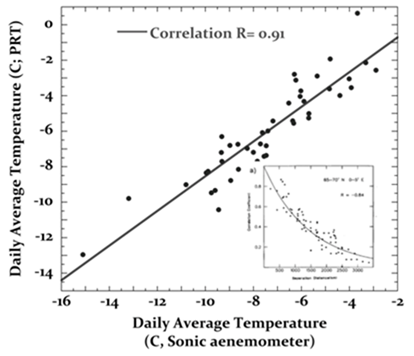
Abbildung 6: Korrelation der RM Young-Temperaturmessungen mit jenen des Schall-Anemometers. Eingebettet: Abbildung 1a aus (14), die Korrelationen von Temperaturaufzeichnungen zeigt von meteorologischen Stationen im terrestrischen Netz 65° bis 70°N, 0° bis 5° E. Bei einer Korrelation von 0,5 beträgt die Länge bis zu 1400 km.

Abbildung 7: Kalibrierungs-Experiment an der University of Nebraska in Lincoln (aus (11), Abbildung 1); E, MMTS shield; F, CRS shield; G, the aspirated RM Young reference.

Abbildung 7 zeigt das screen-type [?] Kalibrierungs-Experiment an der University of Nebraska. Jeder Typ enthielt den identischen HMP45C-Sensor (11). Die Referenz-Temperaturen der Kalibrierung wurden mittels eines belüfteten RM Young PRT erhalten, eingestuft als akkurat bis < ±0.2°C bei einer Sonneneinstrahlung unter 1100 W/m².

Diese unabhängigen Kalibrierungs-Experimente testeten die Auswirkung einer Vielfalt von allgemein verwendeten Typen zur Genauigkeit von Lufttemperatur-Messungen durch PRT (10, 11, 18). Unter den Typen waren auch das allgemeine Cotton Regional Shelter (CRS, Stevenson screen) und der MMTS-Screen, der jetzt allgemein verwendet wird in den USHCN-Daten.

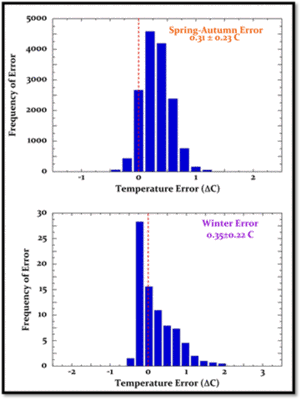
Abbildung 8: Mittlerer systematischer Messfehler eines HMP45C-Sensors innerhalb eines MMTS über einer Gras-Oberfläche (oben) und einer schneebedeckten Oberfläche (unten) (10, 11).

Abbildung 8 oben zeigt den mittleren systematischen Messfehler einer MMTS-Umhüllung, der auf eine PRT-Temperaturmessung angewendet wird. Den Fehler fand man während des Kalibrierungs-Experimentes der Abbildung 7 (11). Abbildung 8 unten zeigt die Ergebnisse einer unabhängigen PRT/MMTS-Kalibrierung über einer schneebedeckten Oberfläche (10). Die mittlere jährliche systematische Unsicherheit, die von dem MMTS erzeugt wird, kann aus diesen Daten berechnet werden zu 1s = 0.32°C ± 0.23°C. Die verzerrte Warm-Bias-Verteilung des Fehlers über Schnee ist größenordnungsmäßig ähnlich der unbelüfteten RM Young-Hülle beim Plaine Morten-Experiment (Abbildung 5).

Abbildung 9 zeigt den mittleren systematischen Messfehler erzeugt von einer PRT-Stichprobe innerhalb einer traditionellen CRS-Umhüllung (11).

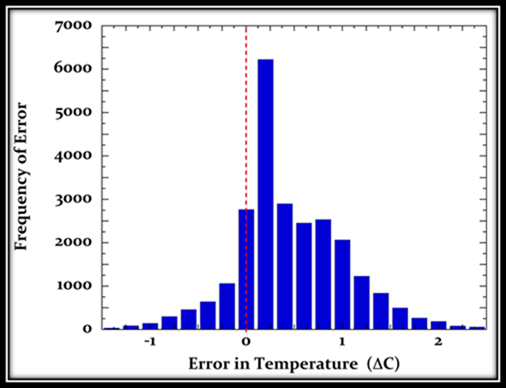
Abbildung 9: der mittlere systematische Tag-Nacht-Messfehler, erzeugt von einer PRT-Temperaturstichprobe innerhalb einer traditionellen CRS-Hütte.

Der Warm-Bias in den Daten ist offensichtlich, ebenso wie die Nicht-Normalverteilung des Fehlers. Die systematische Unsicherheit der CRS-Hütte betrug 1s = 0.44°C ± 0.41°C. Die HMP45C-PRT-Stichprobe ist mindestens genauso akkurat wie das traditionelle LiG-Thermometer innerhalb der Wetterhütte (19, 20). Mittels des PRT/CRS-Experimentes kann man dann eine untere Grenze der systematischen Messunsicherheit abschätzen, der in den Festlands-Temperaturaufzeichnungen im gesamten 19. und fast dem ganzen 20. Jahrhundert enthalten ist.

2.2 Wassertemperatur

Obwohl erhebliche Bemühungen aufgewendet wurden, um die Wassertemperaturen besser zu verstehen (21 bis 28), gab es nur sehr wenige Feld-Kalibrierungs-Experimente der Wassertemperatur-Sensoren. Eimermessungen sowie solche in Kühlwasser von Schiffen ergaben den Hauptanteil von Messungen der Wassertemperatur Anfang und Mitte des 20. Jahrhunderts. Auf Fest- und Treibbojen montierte Sensoren kamen seit etwa 1980 immer stärker zum Einsatz. Inzwischen dominieren sie die Messungen der Wassertemperatur (29). Die Aufmerksamkeit gilt den Kalibrierungs-Studien dieser Instrumente.

Die von Charles Brooks im Jahre 1926 durchgeführten Reihen-Experimente sind bei weitem die umfassendsten Feld-Kalibrierungen von Messungen der Wassertemperatur mit Eimern und im Kühlwasser von Schiffen, die jemals von einem einzelnen individuellen Wissenschaftler durchgeführt worden waren (30). Abbildung 10 zeigt typische Beispiele des systematischen Fehlers dieser Messungen, die Brooks gefunden hatte.

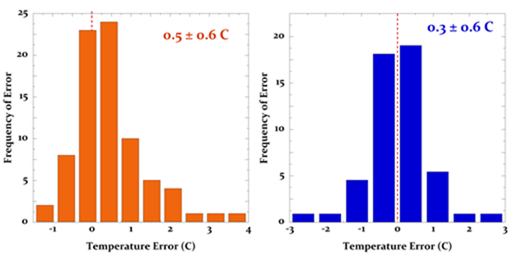
Abbildung 10: Systematischer Messfehler in einem Satz von Messungen der Wassertemperatur im Kühlwasser- (links) und mit Eimermessungen (rechts) wie von Brooks beschrieben (30).

Brooks stellte auch einen Mann ab, der die Messungen an Bord des Schiffes überwachen sollte, nachdem er seine Experimente abgeschlossen hatte und von Bord gegangen war. Die Fehler nach seinem Verlassen des Schiffes waren etwa doppelt so groß als mit ihm an Bord. Die einfachste Erklärung hierfür ist, dass die Sorgfalt schwand, vielleicht zurück zum Normalen, wenn niemand schaute. Dieses Ergebnis verletzt die Standard-Hypothese, dass Fehler von Temperatursensoren für jedes einzelne Schiff konstant sind.

Im Jahre 1963 beschrieb Saur das größte Feld-Kalibrierungs-Experiment von Thermometern in Kühlwasser, durchgeführt von Freiwilligen an Bord von 12 Transportschiffen des US-Militärs, die vor der US-Pazifikküste operierten (31). Das Experiment enthielt auch 6826 Beobachtungs-Paare. Abbildung 11 zeigt die experimentellen Ergebnisse einer Fahrt eines Schiffes.

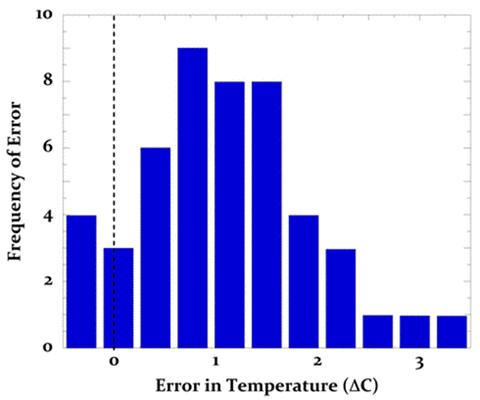
Abbildung 11: Systematischer Fehler in gemessenen Kühlwasser-Temperaturen an Bord eines Militär-Transportschiffes, das im Juni/Juli 1959 operierte. Der mittlere systematische Bias und die Unsicherheit in diesen Daten beträgt 1s = 0.9°C ± 0.6°C.

Saur bezeichnete die Abbildung 11 als „eine typische Verteilung der Unterschiede“, die auf den verschiedenen Schiffen aufgetreten waren. Die ±0.6°C-Unsicherheit hinsichtlich des mittleren systematischen Fehlers ist vergleichbar mit den von Brooks genannten Werten in Abbildung 10.

Saur schloss seinen Bericht mit den Worten: „Der mittlere Bias der gemessenen Meerwasser-Temperaturen beim Vergleich mit den Wassertemperaturen an der Ozeanoberfläche wird innerhalb des 95%-Vertrauensintervalls abgeschätzt mit 0,67°C ± 0,33°C auf der Grundlage einer Stichprobe von 12 Schiffen. Die Standardabweichung der Unterschiede zwischen den Schiffen wird mit 0,9°C geschätzt. Folglich sind die in Gegenwart und Vergangenheit gemessenen Wassertemperaturdaten ohne verbesserte Qualitätskontrolle zum größten Teil nur geeignet für allgemeine klimatologische Studien“. Saurs Sorgfalt ist aufschlussreich, wurde aber offensichtlich von Konsens-Wissenschaftlern missbraucht.

Messungen mittels Bathythermographen (BT) und Einmal-Bathythermographen (XBT) haben ebenfalls bedeutend zu den Wassertemperatur-Aufzeichnungen beigetragen (32). Extensive BT und XBT-Kalibrierungs-Experimente zeigten multiple Quellen systematischer Fehler, hauptsächlich durch mechanische Probleme und Kalibrierungsfehler (33 bis 35). Relativ zu einem reversing Thermometer-Standard [?] zeigten BT-Feldmessungen einen Fehler von ±s = 0.34°C ± 0.43°C (35). Diese Standardabweichung ist mehr als doppelt so groß wie wie die vom Hersteller genannte Genauigkeit von ±0,2°C und reflektiert den Einfluss unkontrollierter Feldvariablen.

Die SST-Sensoren in treibenden und festen Bojen wurden während des 20.Jahrhunderts niemals feld-kalibriert, so dass keine allgemeine Schätzung systematischer Messfehler vorgenommen werden konnte.

Allerdings hat Emery einen 1s = ±0.3°C-Fehler geschätzt mittels eines Vergleichs der Wassertemperatur von Treibbojen, die sich nicht weiter als 5 km voneinander entfernt hatten (28). Wassertemperatur-Messungen bei Entfernungen unter 10 km werden als übereinstimmend betrachtet.

Eine ähnliche Größenordnung des Bojenfehlers von ±0,26°C wurde relativ zu den Wassertemperaturdaten gefunden, die aus Advanced Along-Track Scanning Radiometer (AATSR)-Satellitendaten abgeleitet worden waren. Die Fehlerverteilungen waren nicht-normal.

In noch jüngerer Zeit wurden ARGO-Bojen feld-kalibriert gegen sehr genaue CTD-Messungen (CTD = conductivity-temperature-depth). Sie zeigten mittlere RMS-Fehler von ±0,56°C (37). Dies ist größenordnungsmäßig ähnlich der gemessenen mittleren Differenz von ±0,58°C in buoy-Advanced Microwave Scanning Radiometer (AMSR)-Satellitendaten (38).

3.Diskussion

Bis vor Kurzem (39, 40) waren systematische Temperatursensor-Messfehler niemals erwähnt worden bei der Berichterstattung bzgl. Ursprung, Bewertung und Berechnung der globalen mittleren Lufttemperatur. Auch in Fehleranalysen hatten sie niemals Eingang gefunden (15, 16, 39 bis 46). Selbst nach der Nennung systematischer Fehler in der veröffentlichten Literatur in letzter Zeit wird jedoch das Central Limit Theorem herangezogen um abzuschätzen, dass diese sich zu Null mitteln (36). Allerdings sind systematische Temperatursensor-Fehler weder zufällig verteilt noch zeitlich, räumlich oder von Instrument zu Instrument konstant. Es gibt keinen theoretischen Grund zu erwarten, dass diese Fehler dem Central Limit Theorem folgen (47, 48) oder dass solche Fehler reduziert oder eliminiert werden durch Mittelung multipler Messungen; selbst wenn diese Messungen millionenfach durchgeführt werden. Eine vollständige Inventur der Beiträge zur Unsicherheit in den Aufzeichnungen der Lufttemperatur muss den systematischen Messfehler des Temperatursensors selbst enthalten; tatsächlich muss sie damit beginnen (39).

Die WMO bietet nützliche Ratschläge an hinsichtlich systematischer Fehler (20). Es heißt dort in Abschnitt

1.6.4.2.3 Abschätzung des wahren Wertes – zusätzliche Bemerkungen:

In der Praxis enthalten Messungen sowohl zufällige als auch systematische Fehler. In jedem Falle muss der gemessene mittlere Wert um den systematischen Fehler korrigiert werden, soweit dieser bekannt ist. Wenn man das tut, bleibt die Schätzung des wahren Wertes ungenau wegen der zufälligen Fehler und wegen jedweder unbekannter Komponenten des systematischen Fehlers. Der Unsicherheit des systematischen Fehlers sollten Grenzen gesetzt werden. Sie sollten den Zufallsfehlern hinzugefügt werden, um die Gesamt-Unsicherheit zu ermitteln. Solange jedoch die Unsicherheit des systematischen Fehlers nicht in Wahrscheinlichkeits-Termen ausgedrückt und geeignet mit dem Zufallsfehler kombiniert werden kann, ist das Vertrauensniveau unbekannt. Es ist daher wünschenswert, dass der systematische Fehler vollständig bestimmt wird.

Bei der Erstellung der globalen mittleren Lufttemperatur lagen Angaben der WMO bisher bei der Erstellung der globalen mittleren Temperatur brach.

Systematische Sensorfehler bei Messungen der Luft- und Wassertemperatur waren beklagenswert gering geachtet worden, und es gab nur sehr wenige Feld-Kalibrierungen. Nichtsdestotrotz wird aus den berichteten Fällen klar, dass die Aufzeichnung der Lufttemperatur kontaminiert ist mit einem sehr signifikanten Niveau systematischer Messfehler. Die Nicht-Normalität systematischer Fehler bedeutet, dass die Subtraktion eines mittleren Bias‘ die Messungenauigkeit des globalen Temperaturmittels nicht beseitigen wird.

Außerdem ist die Größenordnung des systematischen Fehlerbias‘ der Messungen von Luft- und Wassertemperatur offensichtlich genauso räumlich und zeitlich variabel wie die Größenordnung der Standardabweichung der systematischen Unsicherheit über den mittleren Fehlerbias. Das heißt, der mittlere systematische Fehlerbias über Schnee auf dem Plaine Morte-Gletscher betrug 2°C, jedoch nur 0,4°C über Schnee in Lincoln, Nebraska. Ähnliche Differenzen wurden von Brooks und Saur auch beim Fehlermittelwert von Kühlwasser gemeldet. Daher wird die Eliminierung eines mittleren Bias‘ um einen geschätzten Betrag immer die Größenordnungs-Mehrdeutigkeit des verbleibenden mittleren Bias‘ hinterlassen. In jeder vollständigen Fehler-Evaluierung wird die verbleibende Unsicherheit des mittleren Bias‘ mit der 1s-Standardabweichung der Messunsicherheit zur Gesamt-Unsicherheit verschmelzen.

Eine vollständige Evaluierung systematischer Fehler liegt jenseits dieser Analyse. Allerdings kann ein Satz geschätzter Unsicherheits-Balken infolge des systematischen Fehlers in der Aufzeichnung der globalen mittleren Lufttemperatur berechnet werden – unter der Voraussetzung, dass die oben beschriebenen Fehler repräsentativ sind (Abbildung 12).

Die Unsicherheits-Bandbreite in Abbildung 12 (rechts) reflektiert ein Verhältnis systematischer Fehler zwischen Wasser- und Festlands-Temperatur von 0,7 zu 0,3. Quadriert bildet die Kombination von Eimer- und Kühlwassermessungen die SST-Unsicherheit vor 1990. Im gleichen Zeitintervall bildete der systematische Fehler der PRT/CRS-Sensoren (39, 40) die Unsicherheit der Festlands-Temperaturen. Treibbojen leisteten einen teilweisen Beitrag (0,25) zu der Unsicherheit bei der Wassertemperatur zwischen 1980 und 1990. Nach 1990 wurde die Fehlerbandbreite weiterhin stetig reduziert, was den zunehmenden Beitrag und die kleineren Fehler der MMTS (Festland) und Treibbojen (Wasseroberfläche) reflektiert.

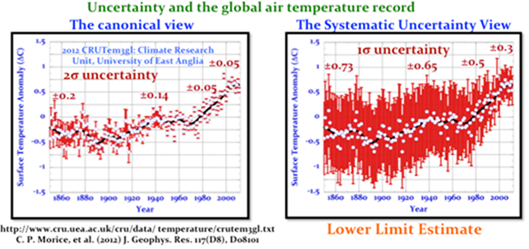
Abbildung 12: Die globale mittlere Lufttemperatur im Jahre 2010, entnommen der Website der Climate Research Unit (CRU), University of East Anglia, UK (hier). Links: Unsicherheits-Bandbreite aufgrund der Beschreibung auf der CRU-Website. Rechts: Fehlerbandbreite der Unsicherheit aufgrund geschätzter systematischer Fehler der Sensormessungen innerhalb der Land- und Wasser-Aufzeichnungen. Weiteres im Text.

Abbildung 12 (rechts) ist sehr wahrscheinlich eine genauere Repräsentation des Wissensstandes als Abbildung 12 (links), jedenfalls was die Rate oder Größenordnung der Änderung der global gemittelten Änderung der Lufttemperatur seit 1850 angeht. Die überarbeitete Unsicherheits-Bandbreite repräsentiert einen nicht-normalen systematischen Fehler. Daher verliert der mittlere Trend der Lufttemperatur jedweden Status als wahrscheinlichster Trend.

Schließlich widmet Abbildung 13 der instrumentellen Auflösung der historischen meteorologischen Thermometer Aufmerksamkeit.

Abbildung 13 provozierte einige wütende Zwischenrufe aus dem Publikum in Sizilien, die nach dem Vortrag gefolgt wurden von einigen sehr groben Angriffen und einer netten E-Mail-Diskussion. Die hier vorgebrachten Argumente waren vorherrschend.

Die instrumentelle Auflösung definiert das Limit der Messgenauigkeit [measurement detection limit]. Beispielsweise waren unter den besten historischen Thermometern vom 19. bis Mitte des 20. Jahrhunderts 1°C-Einteilungen. Die Best-Case-Temperaturauflösung unter Laborbedingungen beträgt daher ±0,25°C. Darüber kann es keinen Streit geben.

Die Standard-Eimermessungen der Wassertemperatur der Challenger-Reise hatte ebenfalls eine 1°C-Abstufung. Damit kommt das gleiche Limit der Auflösung zur Anwendung.

Die besten Thermometer zur Messung des Kühlwassers bei amerikanischen Schiffen enthielten 1°C-Abstufungen; bei britischen Schiffen waren es 2°C. Die beste Auflösung ist demnach ±(0,25 bis 0,5)°C. Dies sind die bekannten Quantitäten. Auflösungs-Unsicherheiten wie systematische Fehler mitteln sich nicht heraus. Kenntnis der Messgrenzen der Instrumente-Klassen gestattet uns die Abschätzung der Auflösungs-Unsicherheit in jeder zusammengestellten historischen Aufzeichnung der Lufttemperatur.

Abbildung 13 zeigt die Grenzen der Auflösung. Darin wird die historische instrumentelle ±2s-Auflösung verglichen mit der ±2s-Unsicherheit in der veröffentlichten Temperatur-Zusammenstellung von Berkeley Earth. Die Analyse lässt sich genauso gut anwenden auf die veröffentlichten Temperaturreihen vom GISS oder der CRU/UKMet, welche die gleichen Unsicherheitsgrenzen aufweisen.

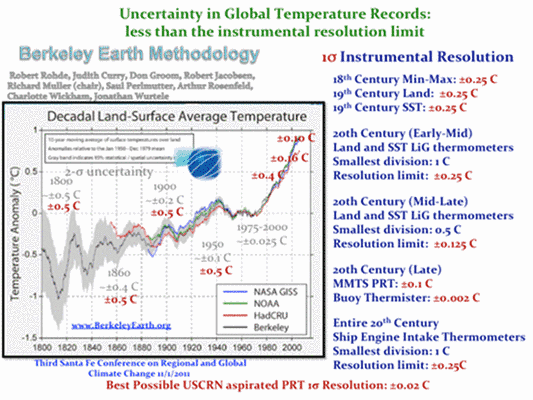
Abbildung 13: Der Trend der globalen gemittelten Lufttemperatur von Berkeley Earth mit den veröffentlichten ±2s-Unsicherheitsgrenzen in grau. Die zeitliche ±2s-Auflösung ist rot eingezeichnet. Rechts findet sich eine Zusammenstellung der best resolution limits in blau der historischen Temperatursensoren, aus denen die globalen Auflösungs-Limits berechnet worden sind.

Die global kombinierte instrumentelle Auflösung wurde mit den gleichen Teilbeiträgen berechnet wie die oben genannte Abschätzung des unteren Limits des systematischen Messfehlers. Das heißt 0,30 zu 0,70 Land- zu Wassertemperatur-Instrumenten, und der veröffentlichte fraktionale Gebrauch jeder Instrumentenart (land: CRS vs. MMTS, and; SS: buckets vs. engine intakes vs. Buoys).

Die Aufzeichnung zeigt, dass während der Jahre von 1800 bis 1860 die veröffentlichten globalen Unsicherheits-Limits von im Feld gemessenen meteorologischen Temperaturen gleich sind der Messungen unter bestmöglichen Laborbedingungen.

Nach etwa 1860 bis zum Jahr 2000 ist die veröffentlichte Auflösung kleiner als die Auflösungs-Limits der Instrumente selbst. Seit mindestens 1860 wurde die Genauigkeit aus dünner Luft hervorgezaubert.

Findet irgendjemand die veröffentlichten Unsicherheiten glaubwürdig?

Alle Ingenieure und Experimentalwissenschaftler könnten nach der Lektüre dieses Beitrags schockiert sein. Zumindest war das bei mir so. Ein Espresso hat mir geholfen.

Die Leute, die die globalen instrumentellen Aufzeichnungen zusammenstellen, haben ein experimentelles Limit stiefmütterlich behandelt, das sogar noch grundlegender ist als systematische Messfehler: Die Messgrenzen [detection limits] ihrer Instrumente. Sie haben dem keinerlei Aufmerksamkeit geschenkt.

Auflösungs-Limits und systematische Messfehler durch das Instrument selbst legen niedrigere Grenzen der Unsicherheit fest. Die in der Konsens-Klimatologie engagierten Wissenschaftler haben beides kaum beachtet.

Das ist fast so, als ob keiner von ihnen jemals eine Messung durchgeführt oder sich jemals mit einem Instrument abgemüht hätte. Es gibt keine andere rationale Erklärung für diese Missachtung als eine ausgeprägte Ignoranz gegenüber experimentellen Verfahren.

Die hier entwickelte Unsicherheits-Abschätzung zeigt, dass die Rate oder die Größenordnung der Änderung der globalen Lufttemperatur seit 1850 nicht genauer bekannt sein kann als mit ±1°C vor 1980 oder innerhalb von ±0,6°C nach 1990, jedenfalls im 95%-Intervall.

Rate und Größenordnung der Temperaturänderung seit 1850 ist buchstäblich unbekannt. Es gibt keinerlei Unterstützung für jedwedes „beispiellos“ in den Aufzeichnungen der Lufttemperatur.

Behauptungen über die höchste Temperatur jemals, selbst auf der Grundlage von 0,5°C-Differenzen, sind völlig unhaltbar und ohne jede Bedeutung.

All diese Debatten um die höchste Lufttemperatur jemals sind nicht besser als theologische Streitereien über das Unaussprechliche. Es sind nach den Worten von William F. Buckley „langweilige Spekulationen über das inhärent Unbekannte“.

Es gibt in den Temperaturaufzeichnungen keinerlei Stützung für irgendwelche Notfälle bzgl. Klima. Außer vielleicht ein Notfall der scheinbaren Kompetenz der AGW-Konsens-Wissenschaftler.

4. Danksagungen: Ich danke Prof. Hendrik Huwald und Dr. Marc Parlange von der Ecole Polytechnique Federale de Lausanne (EPFL), CH-1015 Lausanne, Schweiz, für die großzügige Überlassung der Sensor-Kalibrierungsdaten vom Plaine Morte Gletscher, die Eingang in die Abbildungen 4, 5 und 6 gefunden haben. Diese Arbeit wurde ohne jede externe Zuwendung geleistet.

5. References

[1] JCGM, Evaluation of measurement data — Guide to the expression of uncertainty in measurement 100:2008, Bureau International des Poids et Mesures: Sevres, France.

[2] Frank, P., et al., Determination of ligand binding constants for the iron-molybdenum cofactor of nitrogenase: monomers, multimers, and cooperative behavior. J. Biol. Inorg. Chem., 2001. 6(7): p. 683-697.

[3] Frank, P. and K.O. Hodgson, Cooperativity and intermediates in the equilibrium reactions of Fe(II,III) with ethanethiolate in N-methylformamide solution. J. Biol. Inorg. Chem., 2005. 10(4): p. 373-382.

[4] Hinkley, N., et al., An Atomic Clock with 10-18 Instability. Science, 2013. 341(p. 1215-1218.

[5] Parker, D.E., et al., Interdecadal changes of surface temperature since the late nineteenth century. J. Geophys. Res., 1994. 99(D7): p. 14373-14399.

[6] Quayle, R.G., et al., Effects of Recent Thermometer Changes in the Cooperative Station Network. Bull. Amer. Met. Soc., 1991. 72(11): p. 1718-1723; doi: 10.1175/1520-0477(1991)072<1718:EORTCI>2.0.CO;2.

[7] Hubbard, K.G., X. Lin, and C.B. Baker, On the USCRN Temperature system. J. Atmos. Ocean. Technol., 2005. 22(p. 1095-1101.

[8] van der Meulen, J.P. and T. Brandsma, Thermometer screen intercomparison in De Bilt (The Netherlands), Part I: Understanding the weather-dependent temperature differences). International Journal of Climatology, 2008. 28(3): p. 371-387.

[9] Barnett, A., D.B. Hatton, and D.W. Jones, Recent Changes in Thermometer Screen Design and Their Impact in Instruments and Observing Methods WMO Report No. 66, J. Kruus, Editor. 1998, World Meteorlogical Organization: Geneva.

[10] Lin, X., K.G. Hubbard, and C.B. Baker, Surface Air Temperature Records Biased by Snow-Covered Surface. Int. J. Climatol., 2005. 25(p. 1223-1236; doi: 10.1002/joc.1184.

[11] Hubbard, K.G. and X. Lin, Realtime data filtering models for air temperature measurements. Geophys. Res. Lett., 2002. 29(10): p. 1425 1-4; doi: 10.1029/2001GL013191.

[12] Huwald, H., et al., Albedo effect on radiative errors in air temperature measurements. Water Resorces Res., 2009. 45(p. W08431; 1-13.

[13] Menne, M.J. and C.N. Williams, Homogenization of Temperature Series via Pairwise Comparisons. J. Climate, 2009. 22(7): p. 1700-1717.

[14] Briffa, K.R. and P.D. Jones, Global surface air temperature variations during the twentieth century: Part 2 , implications for large-scale high-frequency palaeoclimatic studies. The Holocene, 1993. 3(1): p. 77-88.

[15] Hansen, J. and S. Lebedeff, Global Trends of Measured Surface Air Temperature. J. Geophys. Res., 1987. 92(D11): p. 13345-13372.

[16] Brohan, P., et al., Uncertainty estimates in regional and global observed temperature changes: A new data set from 1850. J. Geophys. Res., 2006. 111(p. D12106 1-21; doi:10.1029/2005JD006548; see http://www.cru.uea.ac.uk/cru/info/warming/.

[17] Karl, T.R., et al., The Recent Climate Record: What it Can and Cannot Tell Us. Rev. Geophys., 1989. 27(3): p. 405-430.

[18] Hubbard, K.G., X. Lin, and E.A. Walter-Shea, The Effectiveness of the ASOS, MMTS, Gill, and CRS Air Temperature Radiation Shields. J. Atmos. Oceanic Technol., 2001. 18(6): p. 851-864.

[19] MacHattie, L.B., Radiation Screens for Air Temperature Measurement. Ecology, 1965. 46(4): p. 533-538.

[20] Rüedi, I., WMO Guide to Meteorological Instruments and Methods of Observation: WMO-8 Part I: Measurement of Meteorological Variables, 7th Ed., Chapter 1. 2006, World Meteorological Organization: Geneva.

[21] Berry, D.I. and E.C. Kent, Air–Sea fluxes from ICOADS: the construction of a new gridded dataset with uncertainty estimates. International Journal of Climatology, 2011: p. 987-1001.

[22] Challenor, P.G. and D.J.T. Carter, On the Accuracy of Monthly Means. J. Atmos. Oceanic Technol., 1994. 11(5): p. 1425-1430.

[23] Kent, E.C. and D.I. Berry, Quantifying random measurement errors in Voluntary Observing Ships’ meteorological observations. Int. J. Climatol., 2005. 25(7): p. 843-856; doi: 10.1002/joc.1167.

[24] Kent, E.C. and P.G. Challenor, Toward Estimating Climatic Trends in SST. Part II: Random Errors. Journal of Atmospheric and Oceanic Technology, 2006. 23(3): p. 476-486.

[25] Kent, E.C., et al., The Accuracy of Voluntary Observing Ships’ Meteorological Observations-Results of the VSOP-NA. J. Atmos. Oceanic Technol., 1993. 10(4): p. 591-608.

[26] Rayner, N.A., et al., Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. Journal of Geophysical Research-Atmospheres, 2003. 108(D14).

[27] Emery, W.J. and D. Baldwin. In situ calibration of satellite sea surface temperature. in Geoscience and Remote Sensing Symposium, 1999. IGARSS ’99 Proceedings. IEEE 1999 International. 1999.

[28] Emery, W.J., et al., Accuracy of in situ sea surface temperatures used to calibrate infrared satellite measurements. J. Geophys. Res., 2001. 106(C2): p. 2387-2405.

[29] Woodruff, S.D., et al., The Evolving SST Record from ICOADS, in Climate Variability and Extremes during the Past 100 Years, S. Brönnimann, et al. eds, 2007, Springer: Netherlands, pp. 65-83.

[30] Brooks, C.F., Observing Water-Surface Temperatures at Sea. Monthly Weather Review, 1926. 54(6): p. 241-253.

[31] Saur, J.F.T., A Study of the Quality of Sea Water Temperatures Reported in Logs of Ships’ Weather Observations. J. Appl. Meteorol., 1963. 2(3): p. 417-425.

[32] Barnett, T.P., Long-Term Trends in Surface Temperature over the Oceans. Monthly Weather Review, 1984. 112(2): p. 303-312.

[33] Anderson, E.R., Expendable bathythermograph (XBT) accuracy studies; NOSC TR 550 1980, Naval Ocean Systems Center: San Diego, CA. p. 201.

[34] Bralove, A.L. and E.I. Williams Jr., A Study of the Errors of the Bathythermograph 1952, National Scientific Laboratories, Inc.: Washington, DC.

[35] Hazelworth, J.B., Quantitative Analysis of Some Bathythermograph Errors 1966, U.S. Naval Oceanographic Office Washington DC.

[36] Kennedy, J.J., R.O. Smith, and N.A. Rayner, Using AATSR data to assess the quality of in situ sea-surface temperature observations for climate studies. Remote Sensing of Environment, 2012. 116(0): p. 79-92.

[37] Hadfield, R.E., et al., On the accuracy of North Atlantic temperature and heat storage fields from Argo. J. Geophys. Res.: Oceans, 2007. 112(C1): p. C01009.

[38] Castro, S.L., G.A. Wick, and W.J. Emery, Evaluation of the relative performance of sea surface temperature measurements from different types of drifting and moored buoys using satellite-derived reference products. J. Geophys. Res.: Oceans, 2012. 117(C2): p. C02029.

[39] Frank, P., Uncertainty in the Global Average Surface Air Temperature Index: A Representative Lower Limit. Energy & Environment, 2010. 21(8): p. 969-989.

[40] Frank, P., Imposed and Neglected Uncertainty in the Global Average Surface Air Temperature Index. Energy & Environment, 2011. 22(4): p. 407-424.

[41] Hansen, J., et al., GISS analysis of surface temperature change. J. Geophys. Res., 1999. 104(D24): p. 30997–31022.

[42] Hansen, J., et al., Global Surface Temperature Change. Rev. Geophys., 2010. 48(4): p. RG4004 1-29.

[43] Jones, P.D., et al., Surface Air Temperature and its Changes Over the Past 150 Years. Rev. Geophys., 1999. 37(2): p. 173-199.

[44] Jones, P.D. and T.M.L. Wigley, Corrections to pre-1941 SST measurements for studies of long-term changes in SSTs, in Proc. Int. COADS Workshop, H.F. Diaz, K. Wolter, and S.D. Woodruff, Editors. 1992, NOAA Environmental Research Laboratories: Boulder, CO. p. 227–237.

[45] Jones, P.D. and T.M.L. Wigley, Estimation of global temperature trends: what’s important and what isn’t. Climatic Change, 2010. 100(1): p. 59-69.

[46] Jones, P.D., T.M.L. Wigley, and P.B. Wright, Global temperature variations between 1861 and 1984. Nature, 1986. 322(6078): p. 430-434.

[47] Emery, W.J. and R.E. Thomson, Data Analysis Methods in Physical Oceanography. 2nd ed. 2004, Amsterdam: Elsevier.

[48] Frank, P., Negligence, Non-Science, and Consensus Climatology. Energy & Environment, 2015. 26(3): p. 391-416.

[49] Folland, C.K., et al., Global Temperature Change and its Uncertainties Since 1861. Geophys. Res. Lett., 2001. 28(13): p. 2621-2624.

Link: https://wattsupwiththat.com/2016/04/19/systematic-error-in-climate-measurements-the-surface-air-temperature-record/

Übersetzt von Chris Frey EIKE