Wiederholte Versuche zur Autokorrelation und Albedo

Bild rechts: Foto der Szenerie vor dem Haus von Eschenbach (aus seinem Beitrag).

Nehmen wir jetzt einmal an, wir nehmen die gleichen sieben Münzen und werfen alle sieben nicht nur einmal, sondern zehnmal. Wie groß ist die Wahrscheinlichkeit, dass in einem dieser Würfe siebenmal Zahl oben liegt?

Nun kann man auch ohne jede Berechnung sofort erkennen, dass die Chance für ein solches Ergebnis umso größer ist, je öfter man die Münzen wirft. Ich habe die Berechnungen unten als Anhang beigefügt, aber für jetzt wollen wir nur festhalten, dass wenn wir den Münzenwurf nur zehnmal ausführen, die Chance eines zufälligen Ergebnisses von siebenmal Zahl (ein statistisch signifikantes Ergebnis im Signifikanz-Level 99%) von 1% auf 7,5% steigt (nicht im Mindesten statistisch ungewöhnlich).

Kurz gesagt, je mehr Stellen man sich anschaut, umso größer ist die Chance, Seltsamkeiten zu finden, die folglich umso weniger signifikant werden. Praktische Auswirkung hiervon ist, dass man das Signifikanz-Niveau mit der Anzahl der Versuche adjustieren muss. Falls das Signifikanzniveau 95% beträgt, wie es in der Klimawissenschaft üblich ist, dann gilt: Falls man auf 5 Versuche schaut, um ein demonstrativ ungewöhnliches Ergebnis zu bekommen, muss man etwas Bedeutendes im 99%-Niveau finden. Hier folgt eine kleine Tabelle, in der die Anzahl der Versuche mit dem Signifikanz-Niveau verglichen werden, falls man nach dem Äquivalent eines Signifikanz-Niveaus von 95% aus einem einzigen Versuch sucht:

Damit als Prolog folgte ich meinem Interesse am Thema Albedo und untersuchte die folgende Studie mit dem Titel Spring–summer albedo variations of Antarctic sea ice from 1982 to 2009:

Abstract: In dieser Studie wurden die mittleren Albedo-Werte im Frühjahr und Sommer (November bis Februar) sowie deren Trends untersucht unter Verwendung eines Datensatzes, der 28 Jahre lange homogenisierte Satellitendaten für das gesamte Gebiet des antarktischen Meereises enthält sowie für fünf Längengrad-Sektoren rund um die Antarktis: Weddell-See (WS), den Sektor Indischer Ozean (IO), den Sektor Pazifischer Ozean (PO), die Ross-See (RS) und die Bellinghausen-Amundsen-See (BS).

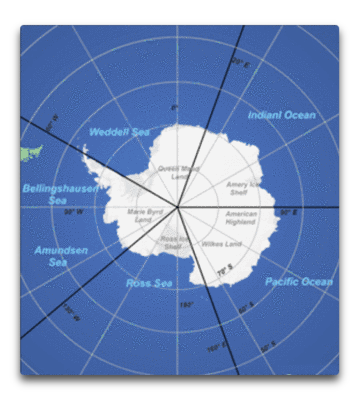
Man erinnere sich: je mehr Stellen man betrachtet, umso wahrscheinlicher wird es, Seltsamkeiten zu finden … wie viele Stellen betrachten sie also?

Nun, zuallererst haben sie den Datensatz offensichtlich in fünf Teile aufgeteilt. Also schauen sie an fünf Stellen. Schon jetzt müssen wir eine Signifikanz von 99% finden, um eine Signifikanz von 95% behaupten zu können.

Allerdings betrachten sie auch nur einen Teil des Jahres. Einen wie großen Teil des Jahres? Nun, das meiste Eis findet sich nördlich von 70°S, so dass messbares Sonnenlicht etwa acht Monate lang darauf fällt. Dies bedeutet, dass sie die Hälfte der zur Verfügung stehenden Albedo-Daten nutzen. Die von ihnen ausgewählten vier Monate sind diejenigen mit dem höchsten Sonnenstand, insofern ist das vernünftig … aber es bleibt die Tatsache, dass sie Daten aussortieren, und dies beeinflusst die Anzahl der Versuche.

Wie auch immer, selbst falls wir die Frage nach der Unterteilung des Jahres vollständig beiseite schieben wissen wir, dass die Karte selbst in fünf verschiedene Teile unterteilt worden ist. Das bedeutet, um eine Signifikanz von 95% zu erhalten muss man etwas finden, dass mit 99% signifikant ist.

Allerdings haben sie tatsächlich gefunden, dass die Albedo in einem der fünf Eisgebiete (der Sektor Pazifischer Ozean) einen Trend aufweist, der beim 99%-Niveau signifikant ist. Ein weiterer Trend (der Sektor Bellinghausen-Amundsen) ist beim 95%-Niveau signifikant. Und dies wären interessante und wertvolle Ergebnisse … außer einem anderen Problem. Das betrifft den Aspekt Autokorrelation.

„Autokorrelation“ bedeutet, wie ähnlich die Gegenwart mit der Vergangenheit ist. Falls die Temperatur an einem Tag -40°C und am nächsten Tag +30°C betragen könnte, würde dies nur eine sehr geringe Autokorrelation zeigen. Aber falls (wie es der Normalfall ist) einem Tag mit einer Temperatur von -40°C ein weiterer eisiger Tag folgt, wäre dies sehr viel Autokorrelation. Und Klimavariablen im Allgemeinen tendieren dazu, autokorreliert zu sein, oftmals erheblich.

Nun, eine Seltsamkeit autokorrelierter Datensätze ist, dass sie dazu tendieren, „trendig“ zu sein. Es ist wahrscheinlicher, einen Trend in autokorrelierten Datensätzen zu finden als in einem Satz mit Zufallsdaten. Tatsächlich fand sich in Zeitschriften vor nicht allzu langer Zeit ein Artikel unter der Überschrift Nature’s Style: Naturally Trendy. (Ich sagte „vor nicht allzu langer Zeit“, aber meine Recherche ergab das Jahr 2005). Es scheint, dass viele Menschen jenes Konzept natürlicher Trendigkeit verstanden haben, wurde doch diese Studie seinerzeit lang und breit diskutiert.

Was weitaus weniger gut verstanden zu sein scheint, ist diese Folgerung:

Da die Natur natürlicherweise trendig ist, ist das Auffinden eines Trends in Messungs-Datensätzen weniger signifikant als es scheint.

In diesem Falle habe ich die Trends digitalisiert. Während ich ihre beiden „signifikanten“ Trends in der Bellinghaus-Amundsen-See bei 95% und im Sektor Pazifischer Ozean bei 99% finden konnte, passend zu meinen eigenen Berechnungen, fand ich unglücklicherweise auch das heraus, was ich vermutet hatte – sie haben Autokorrelation wirklich ignoriert.

Mit ein Grund dafür, warum die Autokorrelation in diesem speziellen Fall so wichtig ist, liegt darin, dass wir mit nur 27 jährlichen Datenpunkten beginnen. Als Ergebnis beginnen wir mit großen Unsicherheiten infolge der geringen Größe der Stichprobe. Der Effekt von Autokorrelation ist, diese schon jetzt unzureichende Stichprobengröße weiter zu reduzieren, so dass das effektive N ziemlich klein ist. Das effektive N [=Anzahl?] für die Bellinghausen-Amundsen-See (BS) beträgt 19 und für den Sektor Pazifischer Ozean (PO) nur 8. Ist Autokorrelation erst einmal berücksichtigt, sind beide Trends überhaupt nicht statistisch signifikant, liegen sie doch beide unter dem 90%-Signifikanz-Niveau.

Führt man zu den Autokorrelations-Effekten noch den Effekt wiederholter Versuche hinzu, bedeutet das im Grunde, dass nicht einer ihrer erwähnten Trends der „Frühjahrs-Sommer-Albedo-Variationen“ statistisch signifikant ist, nicht einmal ansatzweise.

Schlussfolgerungen? Nun, ich muss sagen, dass wir in der Klimawissenschaft unser statistisches Spiel überbieten müssen. Ich bin bei weitem kein Experten-Statistiker. Da sind Personen wie Matt Briggs, Statistician to the Stars, viel besser geeignet. Tatsächlich habe ich nie eine Statistik-Vorlesung besucht. Ich habe mir alles selbst beigebracht.

Falls ich also ein wenig über die Effekte weiß, einen Datensatz nach Signifikanz-Niveaus zu unterteilen, und die Auswirkungen von Autokorrelation auf Trends kenne – wie kommt es dann, dass diese Kerle das nicht wissen? Zur Klarstellung, ich glaube nicht, dass sie es absichtlich tun. Ich glaube, dass es ein echter Fehler ihrerseits war, sie haben einfach nicht den Effekt ihrer Aktionen erkannt. Aber zum Kuckuck, zu sehen, wie Klimawissenschaftler diese gleichen beiden Fehler wieder und immer wieder machen, wird langweilig.

Schließen möchte ich mit einer wesentlich positiveren Anmerkung. Ich erfahre gerade, dass das Magazin Science ein Gremium von Statistikern ins Leben rufen will, das die Einreichungen lesen soll, um ehrliche Fehler vermeiden zu helfen und die Standards von Datenanalysen zu steigern.

Das scheint mir sehr in Ordnung.

—————————————————-

Wiederholte Versuche: Bei der tatsächlichen Berechnung, wie viel besser die Chancen bei wiederholten Versuchen stehen, nutzt man die Tatsache aus, dass falls die Chancen, das etwas passiert, mit X bezeichnet werden (die 1/128 im Falle sieben geworfener Münzen, die dann ,Zahl‘ zeigen), die Chance, dass dann etwas NICHT passiert 1-X, d. h. 1 – 1/128 oder 127/128 beträgt. Es stellt sich heraus, dass die Chance, dass es NICHT passiert bei N Versuchen

(1-X)↑N

ist oder (127/128)↑N. Für N = 10 Würfe von sieben Münzen ergibt sich die Chance, dass NICHT siebenmal ,Zahl‘ erscheint, zu (127/128)↑10oder 92,5%. Dies bedeutet, dass die Chance, dass bei zehn Würfen siebenmal ,Zahl‘ erscheint, 1 minus der Chance ist, dass es nicht passiert, also etwa 7,5%.

Ganz ähnlich, falls wir nach dem Äquivalent eines Vertrauens von 95% in wiederholten Versuchen suchen, beträgt das erforderliche Vertrauensniveau bei N-mal wiederholten Versuchen

0,95↑1/N

Autokorrelation und Trends: Gewöhnlich verwende ich die Methode von Nychka, bei welcher ein „effektives“ N verwendet wird, also eine reduzierte Anzahl von Freiheitsgraden zur Berechnung statistischer Signifikanz.

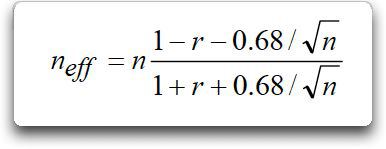
Hier ist n die Anzahl der Datenpunkte, r die Verzögerung minus 1-Autokorrelation und n↓eff das effektive N.

Falls ich jedoch etwas von entscheidender Bedeutung vor mir habe, verwende ich an Stelle von Nychkas heuristischer Methode wahrscheinlich eine Monte-Carlo-Methode. Ich erzeuge beispielsweise 100.000 Beispiele von ARMA (auto-regressive moving-average model) Pseudo-Daten, die gut zur Statistik der aktuellen Daten passen, und ich würde die Verteilung der Trends in jenem Datensatz untersuchen.

Link: http://wattsupwiththat.com/2015/06/27/repeated-trials-autocorrelation-and-albedo/

Übersetzt von Chris Frey EIKE