Können wir eine Aussage darüber machen, ob sich die Ozeane erwärmen?

Die seinerzeitigen Behauptungen zur Genauigkeit, welche heute immer noch unverändert im Raum stehen, kann man in Abbildung 1a (unten) erkennen. Sie stammt aus einer Studie mit dem Titel „Observed changes in top-of-the-atmosphere radiation and upper-ocean heating consistent within uncertainty“ von Norman G.Loeb et al. 2012, paywalled hier, im Folgenden Loeb2012 genannt:

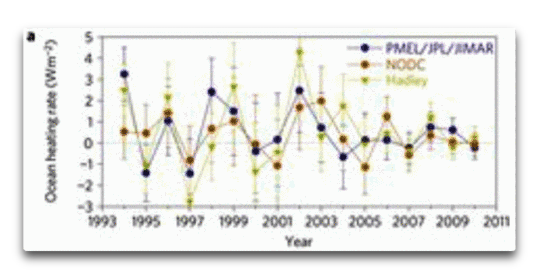
Abbildung 1: Dies ist Abbildung 1(a) aus Loeb2012. Original-Bildunterschrift: a: jährliche gemittelte Erwärmungsraten in den oberen Schichten der Ozeane, berechnet aus Daten von Pacific Marine Environmental Laboratory/Jet Propulsion Laboratory/Joint Institute for Marine and Atmospheric Research (PMEL/JPL/JIMAR), NODC und Hadley, 0–700 m

Ich möchte mich für die Qualität dieser Graphik entschuldigen, aber leider liegt das Dokument hinter einer Zahlschranke. Das ist schon o. k., mich interessierten auch nur deren Fehlerschätzungen.

Wie man sieht, zeigt Loeb2012 die ozeanischen Erwärmungsraten in Watt pro Quadratmeter für jedes Jahr. Alle drei Gruppen nennen die gleiche Fehler-Größenordnung. Der Fehler in den frühsten Daten beträgt etwa 1 W/m². Allerdings beginnt die Größe der Fehler abzunehmen, als die Bojen im Jahre 2006 online gingen. Am Ende ihrer Aufzeichnungen zeigen alle drei Gruppen Fehler deutlich unter einem halben Watt pro Quadratmeter.

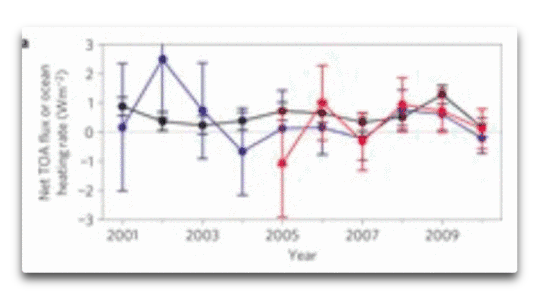
Abbildung 2: Dies ist Abbildung 3(a) aus Loeb2012. In schwarz ist die zur Speicherung verfügbare Wärme dargestellt, abgeleitet aus den CERES-Satellitendaten. In blau sind die Erwärmungsraten bis 1800 m dargestellt und in rot die Erwärmungsraten bis 700 m. Original-Unterschrift: a: globales jährliches Mittel (Juli bis Juni) des Gesamt-TOA-Flusses aus CERES-Beobachtungen sowie die ozeanischen Erwärmungsraten 0 bis 700 sowie 0 bis 1800 m von PMEL/JPL/JIMAR.

Hier erkennt man, dass der Fehler am Ende ihres Datensatzes für die Schicht bis zu einer Tiefe von 1800 Metern ebenfalls unter einem halben Watt pro Quadratmeter lag.

Aber welche Temperaturänderung repräsentiert ein Fehler von einem halben Watt pro Quadratmeter? Meine Faustregel ist einfach.

Ein Watt pro Quadratmeter wärmt einen Kubikmeter Wasser während eines Jahres um 8°C.

(Ja, ich weiß; tatsächlich sind es 8,15°C, aber ich tätige viele allgemeine Berechnungen, so dass ein geringer Fehler-Prozentsatz in Ordnung geht für eine leichtere Berechnung und Speicherung). Das bedeutet, ein halbes Watt pro Quadratmeter schafft in einem Jahr eine Erwärmung von 4°C der gleichen Wassermenge.

Für eine 1800 Meter tiefe Wasserschicht sagt also Loeb2012, dass der Standardfehler ihrer Temperaturmessungen 4°C/1800 m beträgt – macht zwei Tausendstel Grad (0,002°C). Für die dünnere 700 Meter tiefe Schicht – für die der Antriebsfehler der Gleiche, aber die Masse kleiner ist, ergibt sich der gleiche Fehler in W/m² von 4°C/700, was einem alarmierenden Temperaturfehler von 6 Tausendstel Grad (0,006°C) gleichkommt.

Ich sagte zu jener Zeit, dass diese behauptete Genauigkeit um 5 Tausendstel Grad … nun … höchst unwahrscheinlich ist.

Jo Nova weist darauf hin, dass komischerweise die Studie im Jahre 2007 geschrieben worden ist, aber seinerzeit bis heute kaum Aufmerksamkeit erregt hat. Ich hätte sie sicher auch nicht gelesen, als ich meinen o. g. Beitrag geschrieben habe. Die folgenden Abschnitte aus ihrer Studie sind interessant:

Abstract

Wendet man OCCAM auf die typische ARGO-Messdichte an, kommt man zu dem Ergebnis, dass außerhalb der westlichen Begrenzung die monatliche gespeicherte Wärme in der durchmischten Schicht im subtropischen Nordatlantik einen Stichproben-Fehler von 10 bis 20 W/m² aufweist, wenn man über ein Gebiet 10 X 10 mittelt. Dieser Fehler reduziert sich zu weniger als 10 W/m², wenn man die jahreszeitliche Wärmespeicherung berücksichtigt. Fehler dieser Größenordnung zeigen, dass der ARGO-Datensatz interessant ist für die Untersuchung der Variabilität in der durchmischten Schicht in mehrere Jahre langen Zeitmaßstäben. Allerdings erhöht sich der erwartete Stichproben-Fehler auf über 50 W/m² im Gebiet des Golfstromes und nördlich von 40°N, was den Gebrauch von ARGO in diesen Gebieten einschränkt.

Und:

Unsere Analyse von Zufalls-Stichproben von Temperaturfeldern mittels des OCCAM-Modells hat gezeigt, dass das ARGO-Projekt im subtropischen Nordatlantik Temperaturdaten mit einer räumlichen und zeitlichen Auflösung zeigt, dass Ergebnisse einer Stichproben-Unsicherheit bei der Wärmespeicherung in der durchmischten Schicht in einer Größenordnung von 10 bis 20 W/m² liegt. Der Fehler wird kleiner, wenn die betrachtete Periode länger wird und man jahreszeitliche (jährliche) Zeitmaßstäbe nimmt; Reduktion auf 7 ± 1,5 W/m². Innerhalb des Golfstromes und subpolarer Gebiete sind die Stichproben-Fehler viel größer, weshalb der ARGO-Datensatz in diesen Gebieten weniger nützlich ist bei der Untersuchung der Variabilität der Wärmespeicherung in der durchmischten Schicht.

Wieder wollte ich ihre Einheit W/m² in eine Temperaturänderung konvertieren. Das Problem, das ich mit diesen in vielen Studien verwendeten Einheiten habe ist, dass „7 ± 1,5 W/m²“ mir einfach nicht viel sagt. Außerdem messen die ARGO-Bojen nicht W/m², sie messen Temperaturen und konvertieren sie zu W/m². Meine Frage bei der Lektüre der Studie lautete also: um welchen Betrag wird ihr genannter Fehler von „7 W/m²“ die Temperatur der „durchmischten Schicht“ des Nordatlantiks während eines Jahres ändern? Und was meinen sie überhaupt mit durchmischter Schicht?

Nun, sie haben sich ein merkwürdiges Element zum messen ausgesucht. Die „durchmischte Schicht“ ist die oberste Schicht des Ozeans, die sowohl vom Wind als auch dem nächtlichen Umkippen der Ozeane durchmischt wird. Im Klima-Zusammenhang ist dies interessant, weil es sich um den Teil des Ozeans handelt, der auf die sich ändernden Lufttemperaturen darüber reagiert. Die Schicht kann numerisch auf mehrere Arten definiert werden. Im Wesentlichen ist es die Schicht von der Oberfläche bis hinab zur „Thermokline“, also dem Punkt, an dem der Ozean anfängt, sich rasch mit zunehmender Tiefe abzukühlen. Jayne Doucette vom Woods Hole Oceanographic Institute hat eine wunderbare Zeichnung der meisten Dinge angefertigt, die in die durchmischte Schicht eingehen (Aus unbekannten Gründen hat sie eine der wichtigsten Zirkulationen, nämlich das nächtliche Umkippen des oberen Ozeans, weggelassen).

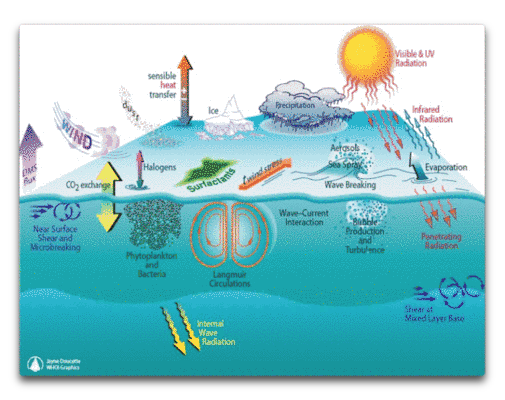
Abbildung 3: Die durchmischte Schicht. Sie zeigt verschiedene physische und biologische Prozesse, die in dieser Schicht ablaufen.

Der Studie zufolge lautet die von ihnen gewählte Definition, dass die durchmischte Schicht bis zu der Tiefe reicht, in der der Ozean um 0,2°C kühler ist als die Temperatur in einer Tiefe von zehn Metern. In Ordnung, kein Problem, das ist eine der Standard-Definitionen … aber wie tief reicht die durchmischte Schicht?

Nun, das Problem ist, dass die Tiefe der durchmischten Schicht sowohl nach Örtlichkeit als auch nach Jahreszeit variiert. Abbildung 4 zeigt typische Variationen in der Tiefe der durchmischten Schicht an einer einzigen Stelle pro Monat.

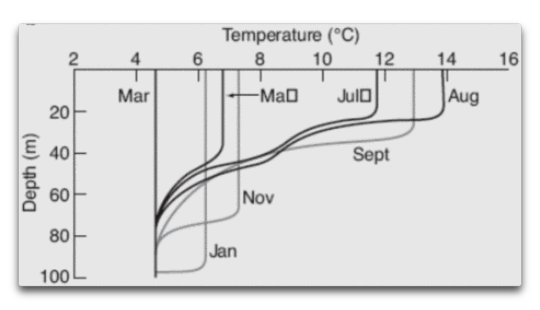
Abbildung 4: Typische Variationen der Tiefe der durchmischten Schicht pro Monat. Tut mir leid, die Stelle für diese Graphik ist nicht bekannt. Hinsichtlich des Temperaturniveaus tippe ich mal auf den Nordatlantik. In jedem Falle ist sie vollständig repräsentativ für die Spezies.

Man erkennt, dass sich die Temperatur bis hinunter zur Thermokline fast gar nicht ändert und danach rasch zurück geht.

Allerdings konnte ich nirgendwo eine Angabe zur mittleren Tiefe der durchmischten Schicht finden. Stattdessen habe ich daher den monatlichen Klimatologie-Datensatz 2°X2° Tiefe der durchmischten Schicht heruntergeladen mit der Bezeichnung „mld_DT02_c1m_reg2.0_Global.nc”. Daraus habe ich das gebietsgewichtete Mittel der Tiefe der durchmischten Schicht entnommen. Es stellte sich heraus, dass die mittleren Tiefen der durchmischten Schicht global etwas unter 60 Metern liegt. Der gesamte Prozess der Berechnungen und des Schreibens des Code nahm eine halbe Stunde in Anspruch … für Interessierte ist der Code beigefügt [im Original!]

Dann habe ich ihren 2°X2°-Datensatz auf ein 1°X1°-Netz umgerechnet, was natürlich hinsichtlich des Mittelwertes die gleiche Antwort lieferte. Aber damit konnte ich meine gewöhnlichen Graphikverfahren verwenden, um die Tiefe darzustellen.

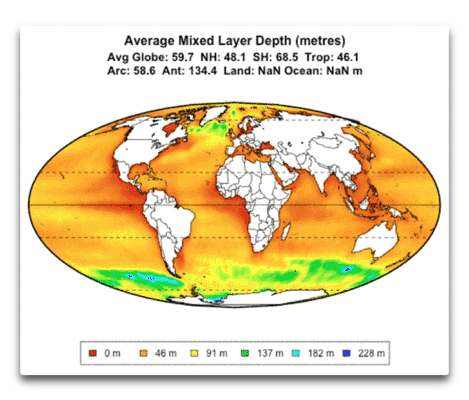
Abbildung 5: Mittlere Tiefe der durchmischten Schicht rund um den Globus. Grüne und blaue Gebiete zeigen tiefer durchmischte Schichten.

Ich liebe die Klimawissenschaft wirklich, weil ich niemals weiß, was ich in Erfahrung bringen muss, um meine Forschungen durchzuführen. Dieses Mal war es die Erkundung der Tiefe der durchmischten Schicht. Wie man sich vorstellen kann, mischen die höchsten Wellen in den stürmischsten Gebieten der Ozeane diesen bis zu größter Tiefe durch, gezeigt in grün und blau. Man erkennt auch das Abbild des El Nino/La Nina entlang des Äquators vor der Küste Ecuadors. Dort blasen die Passatwinde das warme Oberflächenwasser nach Westen und belassen die Thermokline näher an der Oberfläche. So viel kann man daraus lernen … aber ich schweife ab. Ich konnte sehen, dass eine Anzahl seichter Gebiete im Nordatlantik besteht, die zur Durchführung der ARGO-Studie herangezogen wurde. Also berechnete ich die mittlere Tiefe der durchmischten Schicht im Nordatlantik (5°N-65°N, 0°W-90°W). Es ergab sich eine Zahl von 53 Metern, etwa sieben Meter höher als das globale Mittel.

Betrachten wir noch einmal die Faustregel:

Ein Watt pro Quadratmeter über ein Jahr erwärmt einen Kubikmeter Meerwasser um etwa acht Grad.

Berechnet man die Faustregel mit einer Tiefe von 53 Metern, erwärmt ein W/m² über ein Jahr 53 Kubikmeter Wasser (Tiefe der durchmischten Schicht) um etwa 8/53 = 0,15°C. Allerdings geben sie den jährlichen Fehler mit sieben W/m² an (siehe deren obiges Zitat). Dies bedeutet, dass Hadfield2007 sagen, dass die ARGO-Bojen nur die mittlere jährliche Temperatur der durchmischten Schicht im Nordatlantik bestimmen können mit einer Genauigkeit von plus/minus 1°C…

Nun, das scheint mir vernünftig. Es ist sehr, sehr schwierig, die mittlere Temperatur eines stark in Bewegung befindlichen Wasserkörpers genau zu messen, wenn es sich um den Nordatlantik oder irgendeinen anderen Ozean.

So weit, so gut. Jetzt kommt der schwierige Teil. Wir wissen, dass ARGO die Temperatur der durchmischten Schicht im Nordatlantik messen kann mit einem Fehler von ±1°C. Da erhebt sich jetzt folgende Frage: Falls wir den gesamten Ozean mit der gleichen Dichte von Messpunkten wie bei ARGO im Nordatlantik messen könnten, welcher Fehler würde dem finalen Mittelwert innewohnen?

Die Antwort hierauf ruht auf einer seltsamen Tatsache – unter der Annahme, dass die Fehler symmetrisch sind, würde der Fehler des Mittels einer Reihe von Temperaturmessungen, von denen jede seinen eigenen inhärenten Fehler enthält, kleiner sein als der Mittelwert der individuellen Fehler. Falls die Fehler alle gleich – sagen wir – E sind, dann errechnet sich die Größenordnung des Fehlers bei einer Mittelung von N Werten, von denen jeder einzelne den Fehler E aufweist mit

sqrt(N)/N

Beispiel: wenn man 100 Werte mittelt, von denen jeder einzelne den Fehler E aufweist, beträgt der Fehler ein Zehntel E (sqrt(100)/100).

Falls die 118 Fehler andererseits nicht alle gleich sind, dann wird durch sqrt(N)/N nicht der Fehler E angegeben, sondern

sqrt(E^2 + SD^2)

wobei SD die Standardabweichung der Fehler ist.

Jetzt wollen wir für einen Moment annehmen, dass der globale Ozean mit der gleichen Messdichte vermessen wird wie der Nordatlantik in der Studie. Dem ist nicht so, aber ignorieren wir das mal für einen Moment. Betrachtet man die 700 Meter tiefe Schicht, müssen wir bestimmen, wie viel größer das Volumen als das Volumen der durchmischten Schicht im Nordatlantik ist. Folgende Antwort schält sich heraus: der globale Ozean bis zu einer Tiefe von 700 Metern hat 118 mal das Volumen des NA bis 700 m.

Während wir den mittleren Fehler kennen (7 W/m² = 1°C), kennen wir unglücklicherweise nicht die Standardabweichung jener Fehler. Allerdings sagen sie, dass es viele Gebiete mit größeren Fehlern gibt. Falls wir also etwas wie eine Standardabweichung von 3,5 W/m² = 0,5°C annehmen, ist dies vermutlich ein konservativer Wert, der gut und gern auch größer sein kann.

Alles in allem: FALLS wir dir durchmischte Schicht des Nordatlantiks messen können mit einem mittleren Fehler von 1°C und einer Fehler-Standardabweichung von 0,5°C, dann sollten wir in der Lage sein, mit der gleichen Dichte von Messungen den globalen Ozean zu erfassen mit

sqrt(118)/118 * sqrt( 1^2 + 0.5^2 ) = 0.1°C

Jetzt zurück zu Loeb2012, der einen Fehler von irgendwo bei 0,005°C geltend machte … was um einen Faktor 20 zu optimistisch erscheint.

Und meine Vermutung ist: unterschätzt man den tatsächlichen Fehler um einen Faktor 20, ist dies der beste Fall [best case]. Ich sage dies, weil sie bereits gesagt haben, dass der zu erwartende Stichproben-Fehler auf über 50 W/m² im Gebiet des Golfstromes und nördlich von 40°N steigt“. Also gilt ihre Schätzung nicht einmal für den gesamten Nordatlantik.

Ich rede auch vom Best Case, weil dies nahelegt, dass a) die Fehler symmetrisch sind und b) alle Teile des Ozeans mit der gleichen Frequenz wie die oberen 53 Meter des Mittelmeeres erfasst werden. Ich bezweifle, dass irgendetwas davon stimmt, was die Unsicherheit sogar noch größer machen würde.

In jedem Falle bin ich froh, dass wieder einmal die Mainstream-Wissenschaft die interessante Arbeit verifiziert, die hier bei WUWT geleistet wird. Falls Sie sich fragen, was das alles bedeutet, betrachten Sie Abbildung 1 und bedenken Sie, dass die Fehlerbalken in Wirklichkeit zwanzig mal größer sind … dann ist es eindeutig, dass wir nichts darüber sagen können, ob sich die Ozeane erwärmen, abkühlen oder keines von beiden der Fall ist.

Link: http://wattsupwiththat.com/2015/06/06/can-we-tell-if-the-oceans-are-warming/

Übersetzt von Chris Frey EIKE