Das Rätsel der Eiszeiten, Teil 7, Global Circulation Models I
scienceofdoom
Im sechsten Teil ging es um einige der zahlreichen Theorien, die konfuserweise alle unter dem gleichen Namen laufen: die „Milankovitch“-Theorien.
Die Basis all dieser Theorien ist: Obwohl die Änderungen in der Neigung der Erdachse und der Zeitpunkt, in der die Erde der Sonne am Nächsten ist, nicht die Gesamt-Energieeinwirkung der Sonne auf das Klima verändert, verursacht die sich ändernde Verteilung der Energie massive Klimaänderungen über tausende von Jahren. Eine der „klassischen” Hypothesen lautet, dass zunehmende Einstrahlung im Juli bei 65°N die Eisschilde zum Schmelzen bringt. Oder umgekehrt, abnehmende Einstrahlung dort bringt die Eisschilde zum Anwachsen.
Alle hier beschriebenen Hypothesen können ziemlich überzeugend klingen. Das heißt, wenn man sie einzeln für sich betrachtet, klingt jede ziemlich überzeugend – aber wenn man diese „Milankovitch-Theorien“ in ihrer Gesamtheit nebeneinander stellt, klingen sie sämtlich nicht nach viel mehr als nach hoffnungsvollen Gedanken. In diesem Beitrag fangen wir nun an zu betrachten, was GCMs (global circulatio models – kurz "Klimamodelle") dazu tun können, diese Theorien zu falsifizieren. Zu den Grundlagen der GCMs schaue man hier.
Viele Leser dieses Blogs machen sich in verschiedener Weise so ihre Gedanken über GCMs. Aber wie der regelmäßig Kommentare schreibende Leser DeWitt Payne oft sagt: „Alle Modelle sind falsch, aber einige sind nützlich“. Das heißt, keines dieser Modelle ist perfekt, aber einige können etwas Licht auf Klimamechanismen werfen, die wir verstehen wollen. Tatsächlich sind GCMs eine wesentliche Grundlage zum Verständnis vieler Klimamechanismen und zum Verständnis der Wechselwirkungen zwischen verschiedenen Teilen des Klimasystems.
Exkurs: Eisschilde und positive Rückkopplung
Für Anfänger folgt hier ein kleiner Exkurs zu den Eisschilden und zur positiven Rückkopplung. Das Schmelzen und die Neubildung von Eis und Schnee ist unbestreitbar eine positive Rückkopplung im Klimasystem. Schnee reflektiert etwa 60% bis 90% der einfallenden Sonnenstrahlung. Wasser reflektiert weniger als 10% und die meisten Landoberflächen weniger als 25%. Heizt sich eine Region genügend auf, schmelzen Eis und Schnee. Das bedeutet, dass weniger Strahlung reflektiert und mehr Strahlung absorbiert wird, was eine weitere Aufheizung des Gebietes zur Folge hat. Der Effekt „füttert sich selbst“. Es ist eine positive Rückkopplung.
Im jährlichen Zyklus führt dies jedoch nicht zu irgendeiner Art „Runaway“ oder zu einer Schneeball-Erde, weil die Solarstrahlung einen viel größeren Zyklus durchläuft. Über viel längere Zeiträume ist es vorstellbar, dass das (regionale) Abschmelzen von Eisschilden zu mehr (regional) absorbierter Sonnenstrahlung führt, was wiederum mehr Eis zum Schmelzen bringt mit der Folge, dass noch mehr Eis schmilzt. Und umgekehrt gilt das Gleiche für das Anwachsen von Eisschilden. Der Grund, warum dies vorstellbar ist, ist ganz einfach der, dass es der gleiche Mechanismus ist.
Exkurs Ende.
Warum Global Circulation Models (GCM)?
Die einzige Alternative zu GCM’s ist, die Berechnung im Kopf oder schriftlich durchzuführen. Man nehme ein Blatt Papier, plotte den Verlauf der einfallenden Strahlung in allen Breiten während des uns interessierenden Zeitraumes – sagen wir von vor 150 ky bis vor 100 ky (ky = kilo-years = 1000 Jahre) – aufgeschlüsselt nach Jahren, Dekaden oder Jahrhunderten in Abhängigkeit von der Menge des schmelzenden Eises. Dann bestimme man die neue Albedo für jedes Gebiet. Man berechne die Änderung der absorbierten Strahlung und dann die regionalen Temperaturänderungen. Dann berechne man den neuen Wärmetransport von niedrigen in höhere Breiten in Abhängigkeit vom Temperaturgradienten in der jeweiligen Breite, den transportierten Wasserdampf sowie Regen- und Schneemenge. Man vergesse dabei nicht, die Eisschmelze in hohen Breiten zu verfolgen sowie deren Einfluss auf die Meridional Overturning Circulation (MOC), die einen großen Teil des Wärmetransportes vom Äquator zu den Polen treibt. Dann gehe man zum nächsten Jahr, zur nächsten Dekade oder zum nächsten Jahrhundert und wiederhole das Ganze.
Wie machen sich diese Berechnungen?
Ein GCM benutzt einige fundamentale physikalische Gleichungen wie Energie- und Massengleichgewicht. Es benutzt viele parametrisierte Gleichungen, um Dinge zu berechnen wie den Wärmetransport von der Oberfläche in die Atmosphäre abhängig von der Windgeschwindigkeit, Wolkenbildung, Impulstransport durch den Wind in die Ozeane usw. Was immer wir in einem GCM haben, ist besser als die Berechnungen auf einem Blatt Papier (denn dort wird man die gleichen Gleichungen mit viel geringerer räumlicher und zeitlicher Auflösung verwenden müssen).
Falls uns die oben erwähnten „klassischen” Milankovitch-Theorien interessieren, müssen wir die Auswirkungen einer Zunahme von 50 W/m² (über 10.000 Jahre) bei 65°N herausfinden – siehe Abbildung 1 im Teil V. Welche Auswirkungen hat eine simultane Reduktion im Frühjahr bei 65°N? Heben sich die beiden Effekte gegeneinander auf? Ist die sommerliche Zunahme bedeutender als die Reduktion im Frühjahr? Wie schnell sorgt die Zirkulation für eine Verringerung dieser Auswirkungen? Der Wärmetransport von Äquator zu Pol wird getrieben durch die Temperaturdifferenz – wie jeder Wärmetransport. Heizt sich also die Nordpolarregion infolge schmelzenden Eises auf, wird sich die Zirkulation im Ozean und in der Atmosphäre ändern, und weniger Wärme wird polwärts transportiert. Welche Auswirkungen hat das?
Wie schnell schmilzt ein Eisschild bzw. bildet es sich neu? Können die Zu- und Abnahmen der absorbierten Sonnenstrahlung die massiven Eisvorstöße und –rückzüge erklären? Falls die positive Rückkopplung so stark ist, wie geht dann eine Eiszeit zu Ende und wie kann sie 10.000 Jahre später erneut einsetzen? All dies können wir nur mit einem allgemeinen Zirkulationsmodell GCM abschätzen.
Nun gibt es da jedoch ein Problem. Ein typischer GCM-Lauf erstreckt sich über ein paar Modell-Jahrzehnte oder ein Modell-Jahrhundert. Wir brauchen aber einen GCM-Lauf über 10.000 bis 50.000 Jahre. Also brauchen wir 500 mal höhere Rechenleistung – oder wir müssen die Komplexität des Modells reduzieren. Alternativ können wir ein Modell im Gleichgewicht zu einer bestimmten Zeit in der Geschichte laufen lassen um zu sehen, welche Auswirkungen die historischen Parameter auf die uns interessierenden Änderungen hatten.
Frühe Arbeiten
Viele Leser dieses Blogs sind häufig verwirrt durch meinen Ausdruck „alte Arbeiten“ zur Behandlung eines Themas. Warum nimmt man nicht die aktuellste Forschung?
Weil ältere Studien normalerweise das Problem klarer umreißen und detaillierter beschreiben, wie man sich diesem Problem nähert.
Die jüngsten Studien wurden für Forscher vor Ort geschrieben und setzen den größten Teil der bisherigen Erkenntnisse als bekannt voraus – Erkenntnisse, die jedermann vor Ort bereits hat. Ein gutes Beispiel hierfür ist die Studie von Myhre et al. (1998) zum Thema „logarithmische Formel“ für den Strahlungsantrieb durch zunehmenden CO2-Gehalt. Sie wurde auch im IPCC-Zustandsbericht 2001 erwähnt. Diese Studie hat sehr viele Blogger verwirrt. Ich habe viele Blogbeiträge gelesen, in denen die jeweiligen Autoren und Kommentatoren wegen der fehlenden Rechtfertigung des Inhalts dieser Studieihre die metaphorischen Hände gehoben haben. Es ist aber nicht mehr verwirrend, wenn man mit der Physik von Strahlungstransporten vertraut ist sowie mit den Studien aus den siebziger bis zu den neunziger Jahren, in denen das Strahlungs-Ungleichgewicht als Folge von mehr oder weniger „Treibhausgasen“ berechnet wird. Es kommt eben immer auf den Zusammenhang an.
Wir wollen jetzt einen Spaziergang durch einige Jahrzehnte von GCMs machen. Wir beginnen dazu mit Rind, Peteet und Kukla (1989). Sie umreißen die klassische Denkweise des Problems:
Kukla et al. (1981) beschreiben, wie die orbitalen Konfigurationen anscheinend zu den großen Klimavariationen der letzten 150 Millenien passen. Als Ergebnis dieser und anderer geologischer Studien besteht der Konsens, dass orbitale Variationen für die Auslösung eiszeitlicher bzw. zwischeneiszeitlicher Bedingungen verantwortlich sind. Der offensichtlichste Unterschied zwischen diesen beiden Regimes, nämlich die Existenz subpolarer kontinentaler Eisschilde scheinen mit der Sonneneinstrahlung in hohen Breiten der Nordhemisphäre im Sommer korreliert zu sein. Zum Beispiel war die Sonneneinstrahlung im August und September, verglichen mit den heutigen Werten, abgeschwächt, und zwar etwa 116.000 Jahre vor heute (116 ky). Während dieser Zeit begann anscheinend das Wachstum des Eises. Die Sonneneinstrahlung war erhöht um etwa 10.000 Jahre vor heute, während einer Zeit also, in denen sich die Eisschilde rapide zurückzogen (Berger 1978).
Und nun zur Frage, ob Grundlagen-Physik die angenommenen Ursache und Wirkung in Zusammenhang bringen kann:
Sind die solaren Strahlungsvariationen selbst ausreichend, um kontinentale Eisschilde wachsen oder schmelzen zu lassen?
Die Sonneneinstrahlung im Juli bei 50°N und 60°N während der letzten 170.000 Jahre zeigt Abbildung 1, zusammen mit den Werten von August und September bei 50°N (wie der Juli zeigt, traten Fluktuationen bei der Einstrahlung in verschiedenen Breiten in ähnlicher Form auf). Die Spitzen-Variation liegt in der Größenordnung von 10%. Überträgt man dies mit gleicher Prozentzahl auf Änderungen der Lufttemperatur, würden diese in der Größenordnung von 30°C liegen. Das wäre mit Sicherheit ausreichend, um Schnee in den nördlichsten Gebieten von Nordamerika den ganzen Sommer über zu halten, wo die Juli-Temperatur heute nur etwa 10°C über dem Gefrierpunkt liegt. Allerdings ignoriert die direkte Übertragung alle anderen Phänomene, die die Lufttemperatur im Sommer beeinflussen, als da wären Wolkenbedeckung und Albedo-Variationen, langwellige Strahlung, Flüsse am Boden und Advektion.
Verschiedene Energiebilanz-Klimamodelle wurden verwendet, um abzuschätzen, wie groß die Abkühlung in Verbindung mit veränderten Orbitalparametern sein würde. Während sich mit dem Beginn von Eisausdehnung die Oberflächen-Albedo verändert und eine Rückkopplung zur Klimaänderung liefern wird, müssen die Modelle auch grobe Schätzungen einbeziehen, wie die Eisbedeckung sich mit dem Klima ändert. Mit der geeigneten Wahl von Parametern, von denen einige durch Beobachtungen gestützt sind, kann man die Modelle dazu bringen, die großen Klimaänderungen von Eis- und Zwischeneiszeiten zu simulieren.
Allerdings berechnen diese Modelle aus Prinzip nicht all die oben beschriebenen verschiedenen Einflüsse auf die Lufttemperatur, und sie enthalten auch keinen hydrologischen Zyklus, der es zulassen würde, dass sich eine Schneedecke bildet oder ausdehnt. Die tatsächlichen Prozesse, unter denen sich den Sommer über eine Schneedecke halten kann, involvieren komplexe hydrologische und thermische Einflüsse, für welche die einfachen Modelle nur grobe Annäherungen liefern können.
Sie gehen dann näher auf die praktischen Probleme ein, die sich aus der Verwendung von GCMs für Läufe über Tausende von Jahren ergeben, und die wir oben angesprochen haben. Das Problem wird angegangen durch die Verwendung vorgegebener Werte für bestimmte Parameter und durch Verwendung eines groben Gitters von 8 mal 10 Grad und 9 vertikalen Schichten.
Die verschiedenen Modellläufe der GCMs sind typisch für dieses Vorgehen, GCMs zu verwenden, um „das Zeug herauszufinden“ – man versucht, mit verschiedenen Läufen und verschiedenen Änderungen der Parameter zu erkennen, welche Variationen die größten Auswirkungen haben und welche Variationen, falls überhaupt welche, zu den realistischsten Antworten führen:
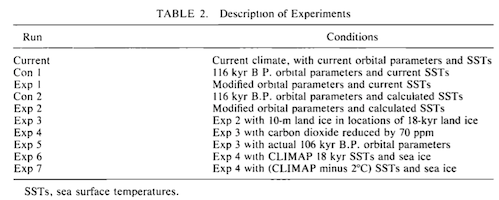
Wir haben also das GCM des GISS für eine Reihe von Experimenten verwendet, in welchen orbitale Parameter, die atmosphärische Zusammensetzung und die Wassertemperaturen verändert worden sind. Wir untersuchen, wie die verschiedenen Einflüsse die Schneebedeckung und Eisschilde beeinflussen, und zwar in den Regionen der Nordhemisphäre, wo während des letzten glazialen Maximums (LGM) Eis gelegen hatte. Soweit wir wissen, ist das GCM generell nicht in der Lage, den Beginn des Wachstums der Eisschilde zu simulieren oder Eisschilde auf dem Niveau des Meeresspiegels, unabhängig von den verwendeten orbitalen Parametern oder der Wassertemperatur.
Und das Ergebnis:
Die Experimente zeigen, dass es eine große Diskrepanz gibt zwischen den Modell-Reaktionen auf Milankovitch-Störungen und der geophysikalischen Beweise des Beginns der Bildung eines Eisschildes. Da das Modell das Wachstum oder den Erhalt von Eisschilden während der Zeit der größten Reduktion der Sonneneinstrahlung in hohen Breiten nicht simulieren konnte (120.000 bis 110.000 Jahre vor heute), ist es unwahrscheinlich, dass es dies zu irgendeiner anderen Zeit innerhalb der letzten vielen hunderttauend Jahre vermocht hätte.
Wenn die Modelläufe korrekt sind, zeigt dies, dass das Wachstum des Eises in einer extrem Wärme absorbierenden Umgebung stattfand. Folglich bedurfte es irgendeiner komplizierten Strategie oder auch irgendwelcher anderen Klimatreiber zusätzlich zum Einfluss der orbitalen Variation (und CO2-Reduktion). Dies würde implizieren, dass wir die Ursache von Eiszeiten und den Zusammenhang mit Milanlovitch nicht wirklich verstehen. Falls das Modell nicht annähernd sensitiv genug auf Klimaantriebe anspricht, kann das Implikationen auf Projektionen künftiger Klimaänderungen haben.
Das grundlegende Modellexperiment hinsichtlich der Fähigkeit von Milankovitch-Variationen, selbst Eisschilde in einem GCM zu bilden (Experiment 2), zeigt, dass im GISS-GCM nicht einmal übertriebene Strahlungsdefizite im Sommer dazu ausreichen. Lässt man ausgedehnte Eisschilde in einer Höhe von 10 m ü. NN eingehen sowie eine CO2-Reduktion um 70 ppm, Zunahme des Meereises bis zu vollen Eiszeitbedingungen und Wassertemperaturen, die auf CLIMAP-Schätzungen vor 18.000 Jahren oder noch niedriger reduziert wurden, ist das Modell kaum in der Lage, diese Eisschilde in begrenzten Gebieten vor dem Schmelzen zu bewahren. Wie wahrscheinlich ist es, dass diese Ergebnisse den aktuellen Stand der Dinge repräsentieren?
Das waren die GCMs des Jahres 1989.
Phillips und Held (1994) hatten im Wesentlichen das gleiche Problem. Das ist der berühmte Isaac Held, der extensiv über Klimadynamik gearbeitet hat sowie über Wasserdampf-Rückkopplung und GCMs. Er betreibt einen sehr lesenswerten exzellenten Blog.
Während paläoklimatische Aufzeichnungen deutliche Beweise zur Stützung der astronomischen oder Milankovitch-Theorie von Eiszeiten liefern (Hays et al. 1976), sind die Mechanismen, mit denen orbitale Änderungen das Klima beeinflussen, immer noch ziemlich schlecht verstanden. Für diese Studie nutzen wir das gemischte Atmosphäre-Ozean-Modell [the atmosphere-mixed layer ocean model]. Bei der Untersuchung der Sensitivität dieses Modells auf unterschiedliche Kombinationen orbitaler Parameter haben wir drei numerische Experimente miteinander verglichen.
Sie beschreiben die Vergleichsmodelle:
Angefangen haben wir mit der Auswahl der beiden Experimente, die vermutlich die größten Unterschiede hinsichtlich des Klimas zeitigen unter Vorgabe der Bandbreite von berechneten Variationen von Parametern, die sich während der letzten paar hunderttausend Jahre ereignet haben. Die Exzentrizität wird in beiden Fällen mit 0,04 gleich gesetzt. Das ist deutlich größer als der gegenwärtige Wert von 0,016, aber vergleichbar mit dem, was es vor 90.000 bis 150.000 Jahren gegeben hat.
Im ersten Experiment werden das Perihel zur Sommer-Sonnenwende der Nordhemisphäre und die Neigung auf den hohen Wert von 24° gesetzt. Im zweiten Fall liegt das Perihel zum Zeitpunkt der Wintersonnenwende auf der Nordhemisphäre, und die Neigung entspricht 22%. Perihel und Neigung begünstigen beide warme Sommer der Nordhemisphäre im ersten Fall und kühle nördliche Sommer im zweiten Fall. Diese Experimente werden jetzt jeweils mit WS bzw. CS bezeichnet.
Dann haben wir eine weitere Berechnung durchgeführt, um zu bestimmen, wie viel der Differenz zwischen diesen beiden Integrationen der Verschiebung des Perihel geschuldet ist und wie viel davon der Änderung der Neigung. In diesem dritten Modell liegt das Perihel zur Sommersonnenwende, aber die Neigung beträgt nur 22°. Die Exzentrizität ist immer noch mit 0,04 angesetzt. Dieses Experiment wird im Folgenden als W22 bezeichnet.
Aber traurigerweise:
Trotz der großen Temperaturänderungen auf dem Festland erzeugt das CS-Experiment keinerlei neue Regionen mit permanenter Schneebedeckung auf der Nordhemisphäre. Die gesamte Schneedecke schmilzt im Sommer vollständig. Folglich ist das Modell, so wie derzeit getrimmt, nicht in der Lage, den Beginn der Bildung von Eisschilden allein aufgrund orbitaler Störungen zu simulieren. Dies ist konsistent mit dem Ergebnissen von Rind mit einem GCM (Rind et al. 1989).
Im nächsten Artikel schauen wir auf günstigere Ergebnisse im ersten Jahrzehnt dieses Jahrhunderts.
http://scienceofdoom.com/2013/11/23/ghosts-of-climates-past-part-seven-gcm-i/
Die bisherigen Teile:
Teil I und II: http://www.eike-klima-energie.eu/climategate-anzeige/das-raetsel-der-eiszeiten-teil-i-und-ii/
Teil III: http://www.eike-klima-energie.eu/climategate-anzeige/das-raetsel-der-eiszeiten-teil-iii-hays-imbrie-shackleton/
Teil IV: http://www.eike-klima-energie.eu/climategate-anzeige/das-raetsel-der-eiszeiten-teil-iv-umlaufbahnen-jahreszeiten-und-mehr/
Teil V: http://www.eike-klima-energie.eu/klima-anzeige/das-raetsel-der-eiszeiten-teil-v-aenderungen-der-ekliptik-und-der-praezession/