Wie es so meine Gewohnheit ist, diese Behauptung zu überprüfen, habe ich mir die Daten besorgt. Also ging ich zum Permanent Service for the Mean Sea Level (PSMSL) und habe alle monatlichen Tidenmessungen von dort heruntergeladen, eine Gesamtzahl von 1413 individuellen Reihen. Nun sagten die Autoren der Studie zu der 60-jährigen Oszillation, sie hätten auf „langzeitliche Tidenaufzeichnungen“ geschaut. Falls wir wirklich nach einem 60-Jahre-Signal suchen, sagt mir meine Daumenregel, dass man einen dreimal längeren Zeitraum dafür braucht, also 180 Jahre, um die Ergebnisse einigermaßen abzusichern. Schlechte Nachrichten … wie sich herausstellt, gibt es nur an zwei der 1413 Zeitreihen, nämlich Brest und Swinemünde, 180 Jahre mit Daten. Also müssen wir uns kürzere Zeitreihen vornehmen, vielleicht die doppelte Zeitspanne von 60 Jahren, die wir untersuchen. Es ist oberflächlich, eine so kurze Zeitreihe zu verwenden, aber vielleicht reicht das ja schon. Es gibt 22 Tiden-Datensätze mit Daten aus 120 oder mehr Jahren. Abbildung 1a zeigt deren erste acht:

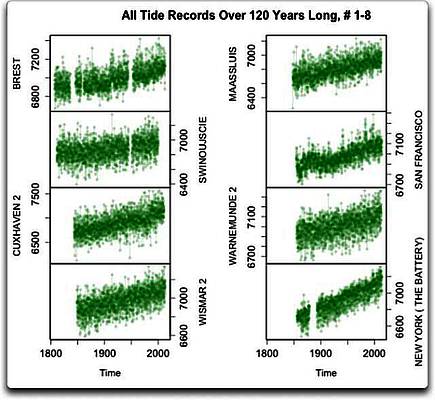
Abbildung 1a: Tidenmessungen über 1440 Monate (120 Jahre) oder mehr. Es handelt sich durchweg um relative Meeresspiegel, das heißt, sie alle beziehen sich auf eine willkürliche Grundlage. Einheiten sind Millimeter. Man beachte, dass die Skalen unterschiedlich und die Trends daher nicht so einheitlich sind wie sie aussehen.
Nun gibt es sicher keinen offensichtlichen 60-Jahres-Zyklus in diesen Tidenaufzeichnungen. Aber vielleicht sind ja die Feinheiten bei dieser Skalierung nicht erkennbar. Daher zeigt die nächste Abbildung die mittleren Gauss-Verteilungen der gleichen Datensätze. Um die darunter liegenden kleinen Änderungen der Mittelwerte zu enthüllen, habe ich zuerst jeden Datensatz trendbereinigt, indem ich jeden linearen Trend entfernt habe. Daher betont Abbildung 1b irgendwelche Zyklen ohne Rücksicht auf deren Größe, und beim Ergebnis muss man die sehr unterschiedlichen Skalierungen zwischen den Abbildungen 1a und 1b beachten.

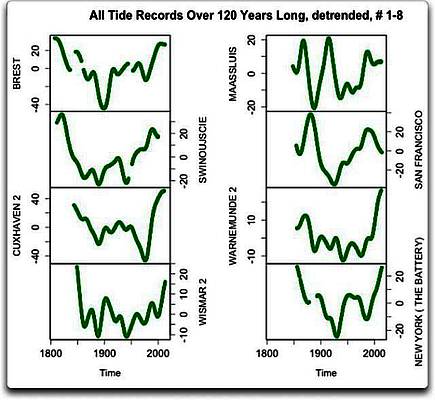
Abbildung 1b: Gauss-Verteilung (14-jährige full-width half-maximum) der linear trendbereinigten acht Zeitreihen von Tidenmessungen aus Abbildung 1a. Man beachte, dass die individuelle Skalierung unterschiedlich zu Abbildung 1a sind.
Nun, sind die Daten erst einmal linear trendbereinigt, zeigen sich alle möglichen Schwingungen. Die dekadischen Schwingungen sind zumeist von der Größenordnung von 20 bis 30 mm von Spitze zu Spitze, obwohl einige etwa doppelt so stark sind. Das große Problem ist, dass die dekadischen Schwingungen unregelmäßig auftreten und völlig verschieden aussehen. Oder für unsere Frage relevant, in keinem dieser Datensätze zeigt sich ein offensichtlicher 60-Jahres-Trend.
Nun können wir noch genauer hinschauen, welche zugrunde liegenden Zyklen in jedem dieser Datensätze vorhanden sind, mit Hilfe einer Periodizitäts-Analyse. Das zeigt, wie stark die einzelnen Zyklus-Längen vertreten sind, in diesem Falle von zwei Monaten bis zu siebzig Jahren. Abbildung 1c zeigt die Periodizitäts-Analyse der gleichen acht langen Datensätze. In jedem Falle habe ich die jahreszeitlichen (jährlichen) Variationen des Meeresspiegels vor der Periodizitäts-Analyse entfernt.

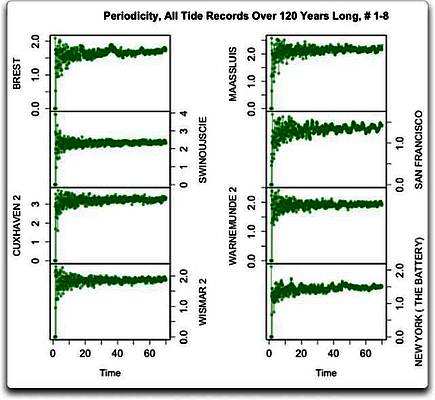
Abbildung 1c: Periodizitäts-Analyse der ersten acht langzeitlichen Tiden-Zeitreihen.
Aber auch da sieht man nicht viel. Oben links in der Zeitreihe von Brest gibt es Hinweise auf einen 38-jährigen Zyklus. New York zeigt eine schwach ausgeprägte Spitze von etwa 48 Jahren. Anderswo zeigt sich durchweg kein Signal in den längerzeitlichen Zyklen, etwa von 30 bis 70 Jahren.
Schauen wir also auf die übrigen 22 Datensätze. Hier folgen die nächsten acht Zeitreihen mit Tidenmessungen in der gleichen Reihenfolge – erst die Rohdaten, dann das Gauss-Mittel und schließlich die Periodizitäts-Analyse.



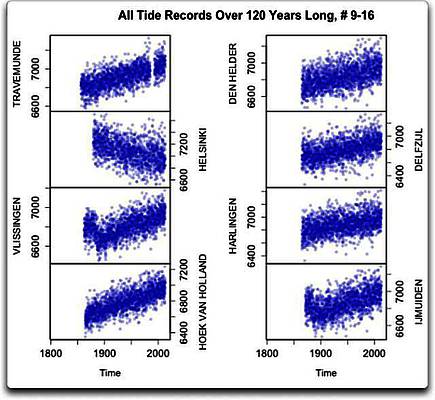
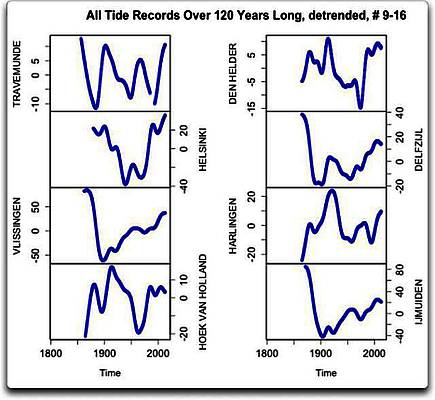
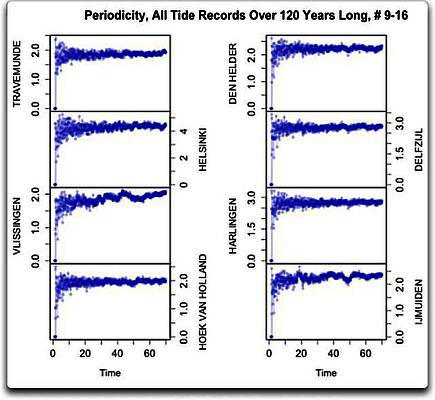
Abbildungen 2a, 2b und 2c: Rohdaten, Gauss-Mittel und Periodizitäts-Analyse der nächsten acht, über 120 Jahre langen Zeitreihen
Und siehe da, es ist das gleiche Problem. Es zeigen sich alle möglichen Arten von Zyklen, aber keiner davon regelmäßig. Das größte Problem ist das Gleiche wie in den ersten acht Datensätzen – die Zyklen sind unregelmäßig und passen außerdem auch nicht zueinander. Mit Ausnahme einer kleinen Spitze bei etwa 45 Jahren in Vlissingen zeigen sich in keinem der längeren Zyklen ausgeprägte Wellen. Also weiter. Jetzt folgen die letzten sechs der 22 über 120 Jahre langen Datensätze:



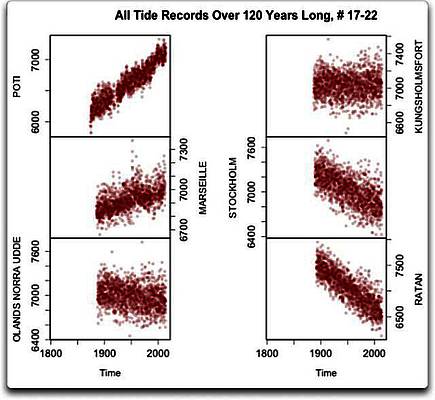
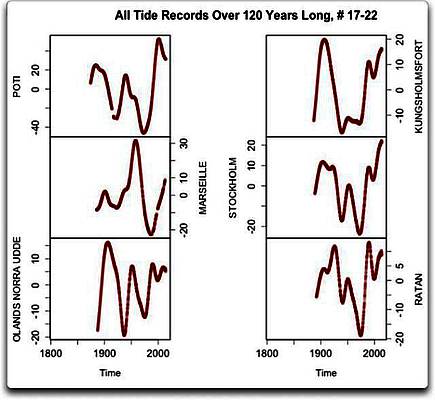
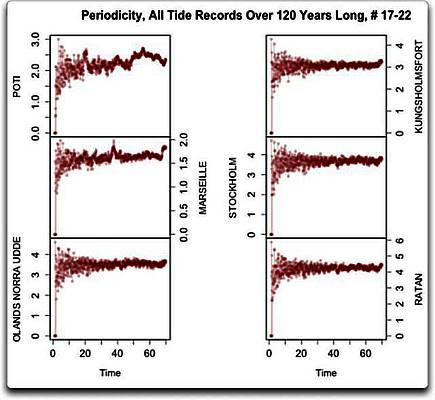
Abbildungen 3a, 3b und 3c: Daten, Gauss-Mittel und Periodizitäts-Analyse wie oben für die letzten sechs der über 120 Jahre langen Tiden-Datensätze.
Da! Fallende relative Meeresspiegel in Abbildung 3a. Offensichtlich haben wir hier einige Tiden-Datensätze vor uns von Stellen mit einer nacheiszeitlichen Landhebung (PGR), das heißt, das Land hebt sich immer noch nach dem Verschwinden von Billionen Tonnen Eis aus der letzten Eiszeit. Folge: das Land hebt sich schneller als der Ozean…
Wie bizarr ist dass denn! Soeben bemerke ich, dass sich die Menschen um den Anstieg des Meeresspiegels als Folge der globalen Erwärmung Sorgen machen – dabei haben wir es hier mit der Hebung der Landmasse als Folge einer globalen Erwärmung zu tun… aber ich schweife ab. Das Gesamtergebnis der PGR in bestimmten Gebieten ist das relative Absinken des Meeresspiegels in vier der sechs Datensätze.
Wie auch in den anderen Datensätzen gibt es in diesen letzten sechs Datensätzen viele Zyklen unterschiedlicher Art, und wie zuvor sind sie nicht regelmäßig und passen auch nicht zueinander. Nur zwei von ihnen zeigen irgend eine Art stärkeres Signal in den längeren Zyklen. In Marseille zeigt sich so etwas mit einer Länge  von etwa 40 Jahren. Und da schau her, in Poti, dem Datensatz links oben, gibt es tatsächlich Hinweise auf einen 60-Jahres-Zyklus… nicht viel, aber von den 22 Datensätzen ist es der einzige, der auch nur einen vagen Hinweis auf ein Signal in der Größenordnung von 60 Jahren zeigt.
Und das ist alles. Das ist das Ergebnis aus allen Datensätzen, die mindestens zweimal so lang sind wie der 60-jährige Zyklus, nach dem wir suchen. Und wir haben grundsätzlich kein Anzeichen eines signifikanten 60-Jahres-Zyklus‘ entdecken können.
Nun nehme ich an, dass man noch weiter graben könnte. Allerdings sind alle verbleibenden Datensätze kürzer – und es tut mir leid, aber in einem Datensatz über 90 Jahre nach einem 60-jährigen Zyklus zu suchen entspricht nicht meiner Ansicht von Wissenschaft auf diesem Planeten. Man kann nicht behaupten, dass es einen Zyklus gibt, wenn man nur Daten der eineinhalbfachen Zykluslänge heranzieht. Das ist einfach Wunschdenken. Ich mag nicht einmal Daten über zwei Zykluslängen, sondern bevorzuge drei davon, aber in dieser Hinsicht gibt es eben nur zwei Datensätze.
Schließlich kann man fragen, ob es möglich ist, alle 22 Datensätze zu mitteln, um so den mysteriösen 66-Jahres-Zyklus zu entdecken? Vielleicht, aber wenn man sich das Durcheinander der oben gezeigten Aufzeichnungen ansieht – würde man es glauben, selbst wenn ich einen solchen Zyklus finden würde? Ich mag nicht einmal daran denken.
Aber als Wissenschaftler fühle ich mich immer durch unbeantwortete Fragen herausgefordert, also mache ich mich an die Arbeit. Ich plane, alle 22 langzeitlichen Datensätze heranzuziehen, diese linear trendbereinigen, sie zu mitteln und die drei Graphen zu zeigen (Rohdaten, Gauss-Mittel und Periodizitäts-Analyse. Das dauert nur einen Moment.
…
Zuerst kommt das Mittel aller trendbereinigten Aufzeichnungen, überlagert mit dem Gauss-Mittel.

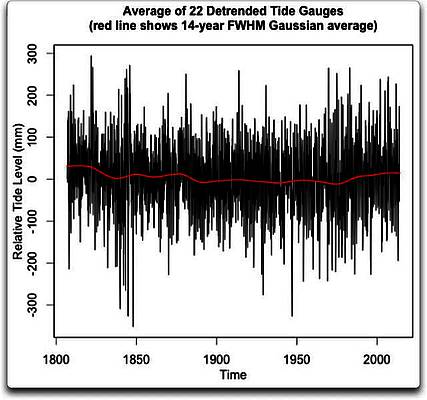
Abbildung 4a: Mittel der trendbereinigten langzeitlichen Tiden-Aufzeichnungen. Die rote Linie zeigt ein full-width half-maximum [?] (FWHM) Gauss-Mittel der Daten, so wie es auch in den Abbildungen 1b, 2b und 3b der Fall war.
Ich sehe nichts, das wie eine Art 60-Jahres-Zyklus aussieht. Hier folgt die Periodizitäts-Analyse der gleichen 22 Stationsdaten:

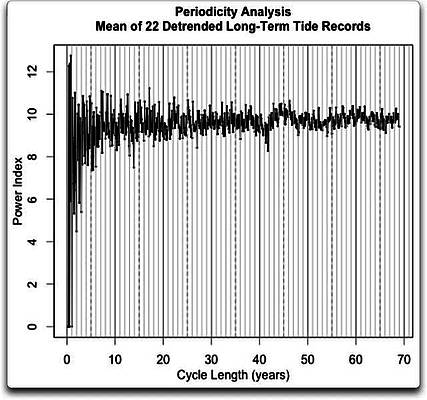
Abbildung 4b: Periodizitäts-Analyse der Daten aus Abbildung 4a.
Wieder nichts! Eine sehr schwache Spitze zeigt sich bei etwa 45 Jahren, die wir auch in einer Einzel-Aufzeichnung gesehen haben. Das ist der einzige langzeitliche Zyklus, den ich erkennen kann.
Schlussfolgerungen? Nun, ich finde den 60-Jahres-Zyklus nicht, über den sie reden, weder in den individuellen noch in den mittleren Daten. Tatsächlich kann ich, wenn überhaupt, nur sehr geringe Anzeichen irgendwelcher langzeitlichen Zyklen erkennen. (Ich finde auch keine Zyklen um 11 Jahre, die in Einklang stehen könnten mit den Zyklen der Sonnenflecken, wie einige Leute behaupten, aber das ist eine andere Frage). Zur Erinnerung, die Autoren haben gesagt:
„Wir kommen zu dem Ergebnis, dass es eine signifikante Oszillation mit einer Periode von rund 60 Jahren bei der Mehrheit der im 20. Jahrhundert durchgeführten Tidenmessungen gibt…“
Tut mir leid, ich kann nichts dergleichen finden. Es gibt in den Einzel-Datensätzen dekadische Schwingungen von etwa 25 bis 50 mm. Ich glaube, man könnte dies „signifikante Oszillationen in der Mehrheit der Tidenmessungen“ nennen, obwohl das sehr weit hergeholt ist.
Aber die „signifikanten Oszillationen” sind nicht gleichmäßig. Man betrachte noch einmal die Gauss-Mittel in den ersten drei Gruppen von Abbildungen. Die „signifikanten Oszillationen“ zeigen sich überall. Selbst innerhalb jeder Einzelaufzeichnung variieren die Schwingungen erheblich hinsichtlich Zykluslänge und Amplitude. Also stimmen die Zyklen in jeder Einzelaufzeichnung nicht einmal mit sich selbst überein.
Auch untereinander stimmen sie nicht überein. Die Schwingungen in den verschiedenen Einzelaufzeichnungen passen weder zeitlich noch hinsichtlich der Größenordnung zusammen.
Und noch mehr auf den Punkt gebracht: keiner zeigt auch nur annähernd ein 60-Jahre-Signal. Nur einer der 22 Datensätze (Poti, oben links in den Abbildungen 3a, 3b und 3c) zeigt ein halbwegs erkennbares 60-Jahres-Signal bei der Periodizitäts-Analyse.
Also sage ich: Ich kann in den 22 langzeitlichen Tiden-Datensätzen keinerlei Anzeichen irgendeines 60-Jahres-Zyklus‘ erkennen. Man beachte, dies unterscheidet sich von der Aussage, dass ein solcher Zyklus in den Datensätzen nicht existiert. Ich sage, dass ich jeden einzelnen auseinander genommen und individuell nach bestem Wissen untersucht habe, und ich war nicht in der Lage, die behauptete „signifikante Oszillation mit einer Periode um 60 Jahre“ in irgendeiner dieser Aufzeichnungen zu finden.
Also gebe ich die Frage jetzt an Sie weiter. Ich habe alle relevanten Dinge verlinkt [siehe Original!] und gebe auch keine Empfehlung für eine bestimmte Analyse. Schauen Sie selbst, ob Sie die Existenz eines vermeintlichen 60-Jahres-Zyklus‘ in den 22 Aufzeichnungen finden.
Viel Glück bei der Suche!
[Es folgen die Hinweise und Links]
Aktualisierung: Ein aufmerksamer Kommentator schrieb dazu Folgendes:
Beim Googeln des Titels fand ich diesen frei zugänglich im Internet hier:
http://www.nc-20.com/pdf/2012GL052885.pdf.
Ich finde ihn überhaupt nicht überzeugend. Sie verwenden die kürzeren Zeitreihen in den PSMSL-Datensätzen und behaupten, 64-jährige Oszillationen zu erkennen, selbst wenn die Zeitreihen nur 110 Jahre lang sind.
Es gibt keinerlei Fourier- oder Periodizitäts-Analysen in dem Artikel.
Jan Kjetil Andersen
Vielen Dank, Jan, ich habe mir diese Studie mal angesehen. Sie verwenden jährlich gemittelte Daten … eine sehr eigenartige Auswahl. Warum sollte man jährliche Mittelwerte verwenden, wenn man bei PSMSL monatliche Datensätze findet?
In jedem Falle besteht das Problem in ihrer Analyse darin, dass man eine Sinus-Kurve an jede zeitliche Periode in den Tiden-Datensätzen anpassen kann und eine Nicht-Null-Antwort erhält. Als Ergebnis ist ihre Methode (Anpassen einer 55-jährigen Sinuswelle an die Daten) bedeutungslos ohne irgendetwas, mit dem man die Daten vergleichen kann.
Nach ein wenig Untersuchung erhält man beispielsweise das folgende Ergebnis. Ich habe ihre Methode verwendet und einen Sinus-Zyklus an die Daten angepasst. Hier folgen die Ergebnisse für Cascais, Aufzeichnung Nr. 43. In ihrer Studie geben sie die Amplitude (von Spitze zu Spitze, wie sich zeigt) der angepassten Sinuskurve mit 22,3 an. Ich erhalte eine ähnliche Antwort, was vermutlich einem etwas unterschiedlichen Optimierungs-Programm geschuldet ist.
Als Erstes möchte ich die von ihnen verwendeten Daten zeigen:

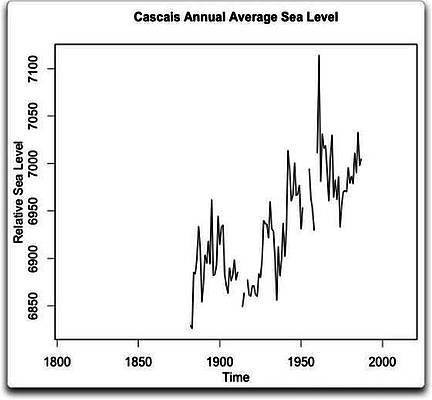
Falls irgendjemand glaubt, daraus einen „~60-Jahres-Zyklus” ableiten zu können, fürchte ich um seinen Geisteszustand…
Nicht nur das, aber nach all ihrem Geschwafel über einen „etwa 60-jährigen Zyklus“ analysieren sie in Wirklichkeit einen 55-jährigen Zyklus. Ist das nicht unlauterer Wettbewerb?
Als Nächstes folgen hier die Ergebnisse ihrer Analyse nach dem Typ einer Sinuswelle für die Perioden von 20 bis 80 Jahren. Die folgende Graphik zeigt die Amplitude von Spitze zu Spitze der angepassten Sinuskurve für jede Periode.

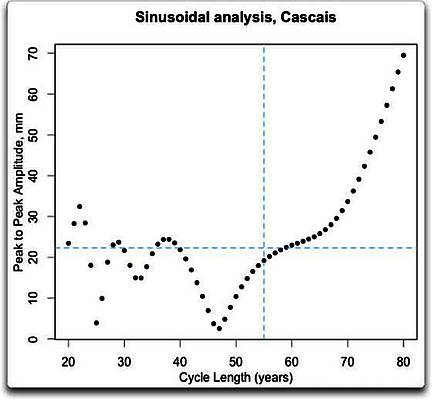
Und tatsächlich zeigt sich ein sinusartiger Zyklus von etwa der Größenordnung von 55 Jahren… aber das unterscheidet sich nicht von den Perioden auf beiden Seiten. Als solches ist das daher bedeutungslos.
Das wirkliche Problem ist: wenn die Zykluslänge im Vergleich zu den Daten so lang wird, ist die Antwort sehr, sehr vage… sie haben weniger als 100 Jahre mit Daten und suchen nach einem 55-jährigen Zyklus. Beklagenswert, um nicht zu sagen unmöglich.
In jedem Falle zeigt ihre Analyse, dass ihre Methode (Anpassen einer 55-jährigen Sinuskurve an die Daten) absolut unbrauchbar ist, weil uns dies nichts über die relative Stärke der Zyklen sagt.
Was natürlich erklärt, warum sie glauben, einen solchen Zyklus gefunden zu haben… ihre Methode ist einfach Unsinn. Wie sich zeigt, ist das Originaldokument noch schlimmer als ich gedacht habe.
Link: http://wattsupwiththat.com/2014/04/25/the-elusive-60-year-sea-level-cycle/
Übersetzt von Chris Frey EIKE

Update 2.5.14:

Autor Willis Eschenbach hat die Behauptung des Auffindens eines etwa 60 jährigen Zyklus nochmals mit einem schärferen Werkzeug ungtersucht: http://wattsupwiththat.com/2014/05/01/the-sea-level-cycles-get-more-elusive/
Er fand alle möglichen Zyklen, doch fast immer verschieden voneinander, nur nicht den behaupteten gemeinsamen 60 jährigen Zyklus