Das Rätsel der Eiszeiten – Teil IV – Umlaufbahnen, Jahreszeiten und mehr
In Teil III haben wir einen kurzen Blick auf die orbitalen Faktoren geworfen, die die Sonneneinstrahlung beeinflussen. Hier nun wollen wir diese Faktoren detaillierter betrachten. Wir beginnen mit der derzeitigen Lage.
Jahreszeitliche Verteilung der einfallenden Sonnenstrahlung
Die Erdachse ist relativ zur Ebene der Umlaufbahn geneigt, so dass im Juli der Nordpol und im Januar der Südpol von der Sonne beschienen wird. In Bild 1 sind die Graphiken der einfallenden Sonnenstrahlen an der Obergrenze der Atmosphäre (TOA), monatlich und auf verschiedenen geographischen Breiten gezeigt:
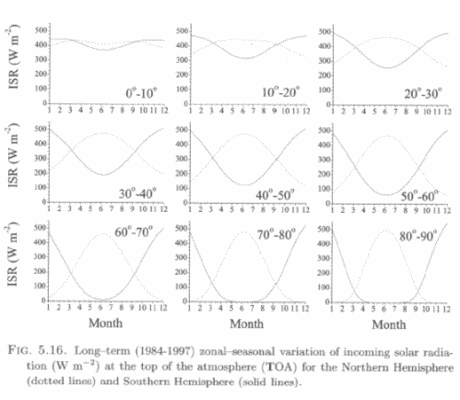
From Vardavas & Taylor (2007)
Abbildung 1: Langzeitliche (1984 bis 1997) zonal-jahreszeitliche Variation der einfallenden TOA-Solarstrahlung (W/m²) der Nordhemisphäre (gepunktete Linie) und der Südhemisphäre (durchgezogene Linie).
Und jetzt die Mittelwerte, zuerst nach Breite für das Jahr, dann Monat für Monat in der Nord-, der Südhemisphäre und des gesamten Globus’:
Figure 2
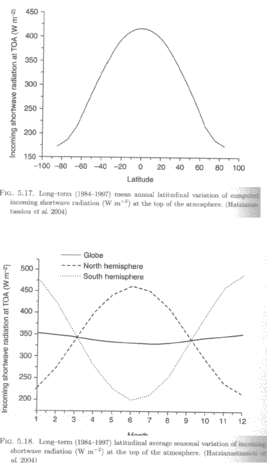
Fig. 2 (5.17): Langzeitliche (1984 bis 1997) mittlere jährliche breitenabhängige Variation der berechneten einfallenden kurzwelligen Strahlung (W/m²) an der TOA (Hatzianatassiou et al. 2004)
Fig. 2 (5.18): Langzeitliche (1984 bis 1997) mittlere jährliche jahreszeitliche Variation der berechneten einfallenden kurzwelligen Strahlung (W/m²) an der TOA (Hatzianatassiou et al. 2004)
Man erkennt, dass die Südhemisphäre einen höheren Spitzenwert aufweist – dies liegt daran, dass die Erde am 3. Januar der Sonne am nächsten ist (Perihel), also während des Sommers der Südhemisphäre. Es spiegelt sich auch im globalen Wert wieder, der zwischen 330 W/m² im Aphel und 352 W/m² im Perihel schwankt.
Exzentrizität
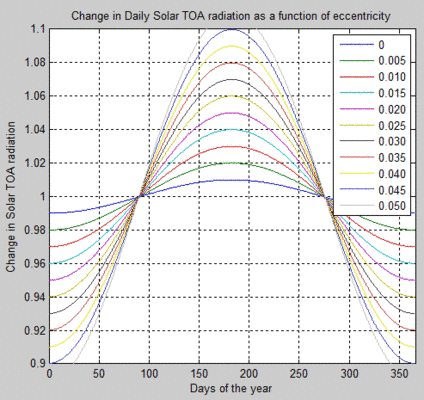
Es gibt eine gute Einführung über planetare Orbits bei Wikipedia. Ich wurde von der langweiligen Aufgabe befreit auszuarbeiten, wie man einen elliptischen Orbit mit der Zeit vermittels Matlab implementiert, hat dies doch freundlicherweise schon Jonathan Levine getan. Er lieferte auch die Lösung des viel schwierigeren Problems der Einstrahlung mit der Breite an irgendeinem Tag während der Quarternary-Periode, auf die wir später schauen werden. In Bild 3 ist die Einstrahlung an der TOA pro Tag des Jahres als Funktion der Exzentrizität des Orbits gezeigt:
Abbildung 3 – aktualisiert
Der Erdorbit weist gegenwärtig eine Exzentrizität von 0,0167 auf. Dies bedeutet, dass die maximale Variation der Solarstrahlung 6,9% beträgt. Im Perihel ist die Erde 147,1 Millionen km von der Sonne entfernt, im Aphel 152,1 Millionen km. Die Menge der Solarstrahlung, die wir empfangen, folgt dem „Umgekehrtes-Quadrat-Gesetz“ – soll heißen, wenn man sich zweimal so weit entfernt, reduziert sich die Sonnenstrahlung um den Faktor vier. Damit kann man die Differenz zwischen Minimum und Maximum sehr einfach berechnen: (152.1/147.1)² = 1.069 oder eine Änderung um 6,9%. Während der letzten Million Jahre oder mehr hat der Erdorbit seine Exzentrizität verändert, und zwar von einem Tiefstwert nahe Null bis zum einem Maximum von etwa 0,055. Die Periode eines jeden Zyklus‘ beträgt etwa 100.000 Jahre.
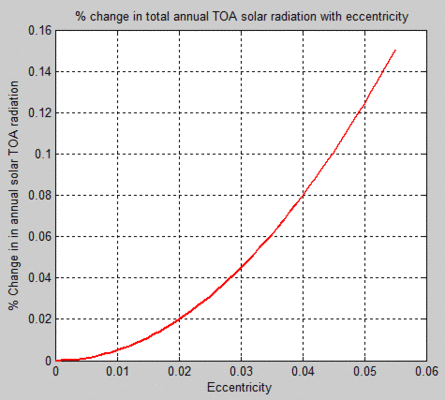
Hier folgt meine eigene Berechnung der Änderung der Gesamtsolarstrahlung an der TOA in Abhängigkeit von der Exzentrizität:
Figure 4
Schaut man auf Abbildung 1 von Imbrie & Imbrie (1980), zeigt sich über den Daumen gepeilt, dass sich die Exzentrizität über einen Zeitraum von 50.000 Jahren von 0,05 auf 0,02 geändert hat (von vor etwa 220.000 Jahren bis vor 170.000 Jahren). Dies bedeutet, dass die solare jährliche Einstrahlung über 50.000 Jahre um 0,1% oder 3 mW/m² pro Jahrhundert zurückgegangen ist. (Dieser Wert ist eine Überschätzung, weil es sich um den Spitzenwert der Sonne senkrecht über uns handelt. Falls wir stattdessen die Sommermonate in höheren Breiten betrachten, ergibt sich eine Änderung von 0,8 mW/m² pro Jahrhundert).
Das ist ein erstaunlicher Rückgang, und da ist es kein Wunder, dass es so schwierig ist, den starken 100.000-Jahres-Zyklus in der Klimahistorie mit den Milankovitch eccentricity cycles in Einklang zu bringen.
Neigung & Präzession
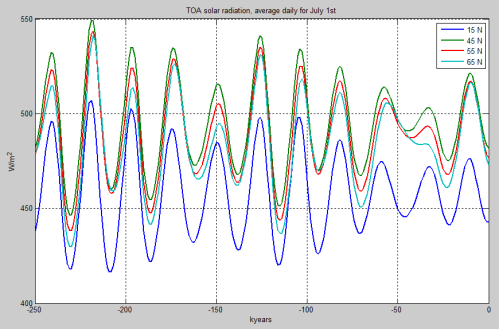
Um die Grundlagen dieser Änderungen zu verstehen, schaue man auf den Milankovitch-Artikel. Keiner dieser beiden Effekte, Neigung und Präzession, ändert die gesamte jährliche Solarstrahlung an der TOA. Sie ändern lediglich deren Verteilung. Die folgende Abbildung 5 zeigt die letzten 250.000 Jahre der solaren Einstrahlungen am 1. Juli – für einige Breiten:
Figure 5
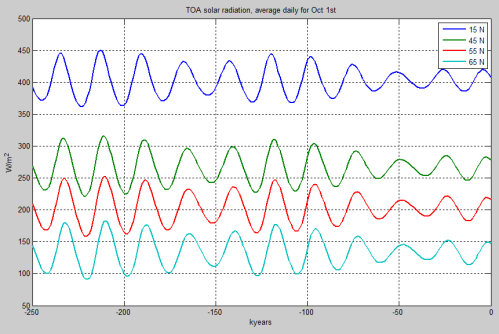
Man beachte, dass im Mittsommer die äquatoriale Einstrahlung natürlich geringer ist als die polare Einstrahlung. In Bild 6 folgt der gleiche Plot für den 1. Oktober. Jetzt ist der äquatoriale Wert höher:
Figure 6
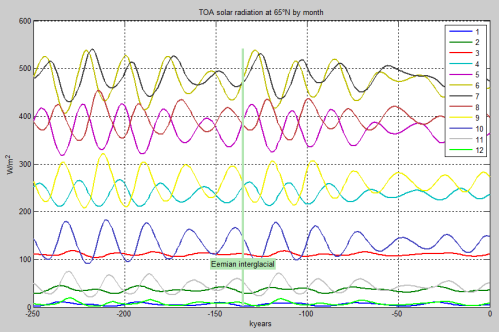
In Bild 7 wollen wir die Werte bei 65°N betrachten, die oft bei Studien zum Thema Eiszeit eine Rolle spielen, dieses Mal jedoch für den Anfang jeden Monats. Das heißt für die Legende: 1 = 1. Januar, 2 = 1. Februar und so fort:
Figure 7
Nur interessehalber habe ich ein Datum der letzten Zwischeneiszeit markiert – die Eemian-Zwischeneiszeit, soweit sie bekannt ist.
Man bilde eine Theorie aus den folgenden Daten:
● Spitzenwert der Einstrahlung bei 65°N
● Höchste Änderungsrate
● minimale Einstrahlung
● Mittelwert der Sommermonate
● Mittelwert des Winterhalbjahres
● Mittelwert der 3 Herbstmonate
Dann gehe man damit in die Graphik. Schwierigkeiten? Man wähle eine andere Breite. Oder Südhemisphäre – auch kein Problem. Wie wir sehen werden, gibt es eine Menge Theorien, die sich alle „Milankovitch“ nennen, aber jede einzelne ist offensichtlich nicht kompatibel mit anderen Theorien gleichen Namens „Milankovitch“.
Endlich haben wir ein Tool, freundlicherweise zur Verfügung gestellt von Jonathan Levine, das es uns erlaubt, jedweden Wert zu berechnen. Wenn also irgend ein Leser einen Wunsch nach anderem output hat, einfach nachfragen. Aber: Warnung an aufstrebende Theoretiker hinsichtlich Eiszeiten (hoffentlich gibt es solche schon) von Kukla et al (2002):
Das marine Isotop wird normalerweise an die astronomische Chronologie angepasst, repräsentiert durch die TAA-Einstrahlung im Juni auf einer Breite von 60° oder 65°N. Das war ausreichend gerechtfertigt, weil die Frequenz der globalen Klimazustände im Pleistozän zu den Frequenzen orbitaler Variationen passt.
Der Mechanismus der Reaktion des Klimas auf die Einstrahlung bleibt unklar, und die Rolle der Einstrahlung in den hohen Breiten im Gegensatz zu derjenigen in niedrigen Breiten ist immer noch Gegenstand von Diskussionen.
In jedem Falle scheint die Verbindung zwischen den globalen Klimata und orbitalen Variationen kompliziert zu sein und ist nicht direkt abhängig von der Einstrahlung im Juni bei 65°N. Wir raten dringend davon ab, lokale Klimaproxys mit Hilfe von unbegründeten astronomischen Variationen vorzunehmen.
Ich bin hinsichtlich historischer Aufzeichnungen und wie sie konstruiert worden sind, ein Novize. Aber ich verstehe, dass SPECMAP zu einer Milankovitch-Theorie gemacht worden ist, das heißt, die Höhepunkte der Eis- und Zwischeneiszeiten wurden zeitlich durch astronomische Werte bestimmt.
Die bisherigen Teile:
Teil I und II: http://www.eike-klima-energie.eu/climategate-anzeige/das-raetsel-der-eiszeiten-teil-i-und-ii/