Ein Modell, eine Wahl

Durch die gute Arbeit von Nic Lewis und Piers Forster, denen ich sehr danke, habe ich ein Set von 20 passenden Modell-Antriebs-Inputs und korrespondierende Temperatur-Outputs erhalten, wie sie vom IPCC benutzt werden. Das sind die individuellen Modelle, deren Mittelwert ich in meinem Beitrag mit dem Titel Model Climate Sensitivity Calculated Directly From Model Results [etwa: Klimasensitivität der Modelle direkt berechnet aus Modellergebnissen] behandelt habe. Ich dachte mir, zuerst die Temperaturen zu untersuchen und die Modellergebnisse mit dem Datensatz HadCRUT und anderen zu vergleichen. Begonnen habe ich mit dem Vergleich der verschiedenen Datensätze selbst. Eine meiner bevorzugten Werkzeuge zum Vergleich von Datensätzen ist der „Violin-Plot“. Abbildung 1 zeigt einen Violin-Plot eines Datensatzes mit Zufallswerten, also eine Gauss’sche Normalverteilung.

Abbildung 1 (rechts): Violin-Plot von 10.000 Zufalls-Datenpunkten mit einem Mittel von Null und Standardabweichung.

Man erkennt, dass die Form einer „Violine“, also der orangefarbene Bereich, aus zwei bekannten „Glockenkurven“ zusammengesetzt ist, die vertikal Rücken an Rücken angeordnet sind. In der Mitte gibt es einen „Kasten-Plot“, welches der Kasten ist, dessen whiskers sich nach oben und unten erstrecken. Die Ausreißer, die sich oben und unten über den Kasten hinaus erstrecken, haben die gleiche Höhe wie der Kasten, eine Distanz, die bekannt ist unter der Bezeichnung „interquartiler Bereich“, weil er sich vom ersten bis zum letzten Viertel der Daten erstreckt. Die dicke schwarze Linie zeigt nicht das Mittel, sondern den Median der Daten. Der Median ist der Wert in der Mitte des Datensatzes, wenn man den Datensatz nach Größe sortiert. Als Folge wird er weniger durch Ausreißer beeinflusst als das Mittel des gleichen Datensatzes.

Kurz gesagt, ein Violin-Plot ist ein Paar spiegelbildlicher Dichteplots, das zeigt, wie die Daten verteilt sind, hinterlegt mit einem Kasten-Plot. Mit diesem Prolog wollen wir uns jetzt ansehen, was uns Violin-Plots über den Temperatur-Output der zwanzig Klimamodelle sagen können.

Für mich ist eines der bedeutendsten Merkmale [metrics] jedes Datensatzes der „erste Unterschied“. Dabei handelt es sich um die Änderung eines gemessenen Wertes zum nächsten. In einem Jahres-Datensatz wie den Temperatur-Modelloutputs besteht der erste Unterschied eines Datensatzes aus einem neuen Datensatz, der die jährliche ÄNDERUNG der Temperatur zeigt. Mit anderen Worten, um wie viel wärmer oder kälter ist die gegebene Temperatur eines Jahres im Vergleich zum Vorjahr? Sehen wir in der realen Welt und in den Modellen große oder kleine Änderungen?

Diese Änderung bei einigen Werten wird oft mit dem Symbol Delta „∆” bezeichnet, was die Differenz in einigen Messungen im Vergleich zum vorigen Wert bedeutet. Zum Beispiel würde man die Änderung der Temperatur mit „∆T” bezeichnen.

Fangen wir also an mit der Betrachtung der ersten Unterschiede der modellierten Temperaturen ∆T. Abbildung 2 zeigt einen Violin-Plot des ersten Unterschiedes ∆T in jedem der 20 Modell-Datensätze, also mit 1 : 20, plus dem HadCRUT-Datensatz und den Zufalls-Normal-Datensätzen.

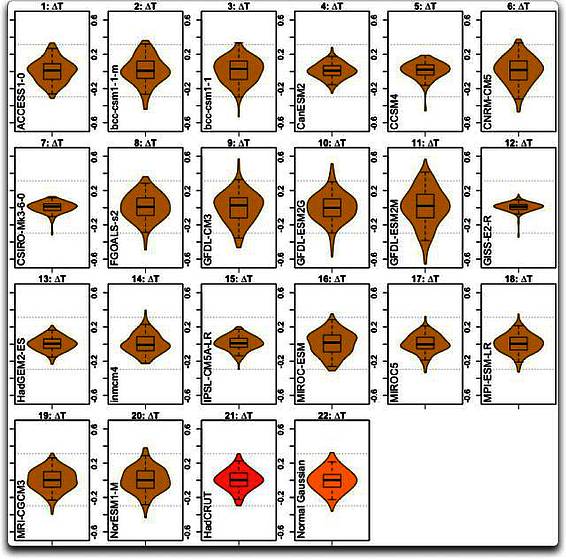
Abbildung 2: Violin-Plots von 20 Klimamodellen (beige) plus dem Beobachtungs-Datensatz HadCRUT (rot) und einem normalverteilten Gauss’schen Datensatz (orange) zum Vergleich. Horizontale gepunktete Linien in jedem Fall zeigen die Gesamt-Bandbreite des HadCRUT-Datensatzes.

Nun… als Erstes fällt auf, dass wir hier sehr, sehr unterschiedliche Verteilungen sehen. Man betrachte zum Beispiel GDFL (11) und GISS (12) im Vergleich zu den Beobachtungen…

Was bedeuten nun die Unterschiede zwischen den Mittelwerten von GDFL und GISS, wenn wir auf die Zeitreihe ihrer modellierten Temperaturen schauen? Abbildung 3 zeigt die beiden Datensätze, GDFL und GISS zusammen mit meiner Nachbildung jedes Ergebnisses.

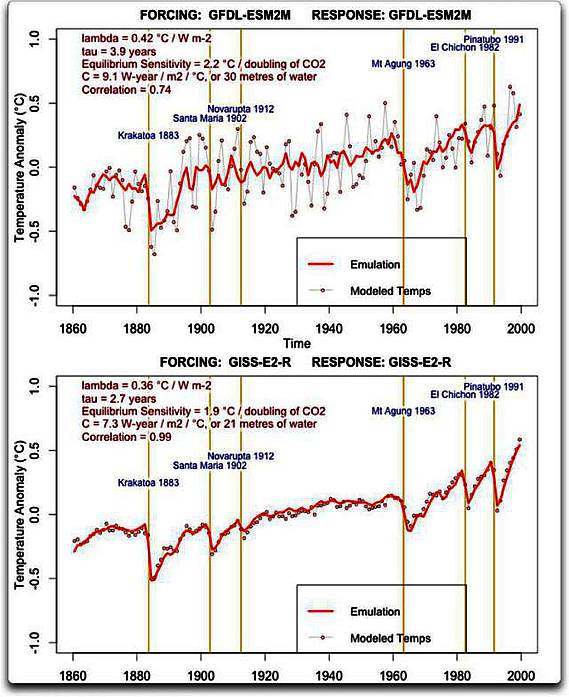
Abbildung 3: Modellierte Temperaturen (gepunktete graue Linien) und Nachbildungen von zwei Modellen, GDFL-ESM2M und GISS-E2-R. Das Verfahren der Nachbildung wird im ersten Link oben des Beitrags erläutert. Zeitpunkte zwei wesentlicher Vulkanausbrüche sind als vertikale Linien eingezeichnet.

Der Unterschied zwischen den beiden Modell-Outputs tritt ziemlich deutlich hervor. Es gibt nur eine geringe Variation von Jahr zu Jahr bei den GISS-Ergebnissen, halb so groß oder noch kleiner, als wir es in der realen Welt beobachten. Andererseits zeigen sich sehr große Variationen von Jahr zu Jahr bei den GDFL-Ergebnissen, bis zu zweimal so groß wie die größte jährliche Änderung, die jemals in den Aufzeichnungen aufgetreten war…

Nun ist es offensichtlich, dass die Verteilung jedweder Modellergebnisse nicht identisch sein wird mit den Beobachtungen. Aber einen wie großen Unterschied können wir erwarten? Um dies zu beantworten, zeigt Abbildung 4 einen Satz mit 24 Violin-Plots von Zufalls-Verteilungen, und zwar mit der gleichen Anzahl von Datenpunkten (140 Jahre mit ∆T) wie die Modell-Outputs.

Abbildung 4: Violin-Plots verschiedener Randwert-Datensätze mit einer Beispielgröße von N = 140, und die gleiche Standardabweichung wie im HadCRUT-∆T-Datensatz.

Wie man sieht, kann man schon mit einer kleinen Beispiel-Auswahl von 140 Datenpunkten eine Vielfalt von Formen erhalten. Das ist eines der Probleme bei der Interpretation von Ergebnissen aus kleinen Datensätzen: man kann kaum sicher sein, was man sieht. Allerdings gibt es ein paar Dinge, die sich nicht groß ändern. Die interquartile Distanz (die Höhe des Kastens) variiert nicht sehr stark. Und auch nicht die Stellen, an denen die Ausreißer enden. Wenn man jetzt die modellierten Temperaturen von GDFL (11) und GISS (12) untersucht (wie sie in Abbildung 5 der Bequemlichkeit halber noch einmal gezeigt werden), kann man sehen, dass sie in keiner Weise irgendeinem der Beispiele normalverteilter Datensätze ähneln.

Es gibt noch einige weitere Merkwürdigkeiten. Abbildung 5 enthält drei andere Beobachtungs-Datensätze – den globalen Temperaturindex von GISS sowie die Datensätze von BEST und CRU ausschließlich vom Festland.

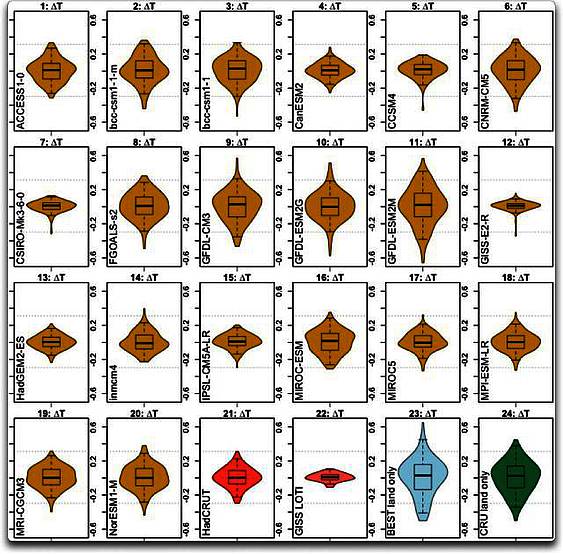
Abbildung 5: Wie Abbildung 2, aber diesmal mit den Temperatur-Datensätzen GISS, BEST und CRUTEM unten rechts. Die horizontalen gepunkteten Linien zeigen die Gesamt-Bandbreite des HadCRUT-Beobachtungs-Datensatzes.

Hier können wir eine merkwürdige Konsequenz der Manipulation der Modelle erkennen. Ich habe noch nie gesehen, wie stark das gewählte Ziel die Ergebnisse beeinflusst. Man bekommt unterschiedliche Ergebnisse abhängig davon, welchen Datensatz man auswählt, an den man das Klimamodell anpasst … und das GISS-Modell (12) wurde offensichtlich frisiert, um die GISS-Temperaturaufzeichnung zu spiegeln (22). Es sieht so aus, als hätten sie sie ziemlich gut frisiert, um zu jenen Aufzeichnungen zu passen. Und mit CSIRO (7) könnte es das Gleiche sein. In jedem Falle sind das die einzigen beiden, die eine ähnliche Form haben wie die globale Temperaturaufzeichnung von GISS.

Und schließlich sehen die beiden Datensätze nur mit Festlandswerten (23, 24, in Abbildung 5 unten rechts) ziemlich ähnlich aus. Man beachte jedoch die Unterschiede zwischen den beiden globalen Datensätzen HadCRUT (21) und GISS LOTI (22) sowie den beiden Festlands-Datensätzen BEST (23) und CRUTEM (24). Man erinnere sich, das Land erwärmt sich schneller als die Ozeane und kühlt sich auch schneller wieder ab. Wie man also erwarten würde, gibt es größere jährliche Schwingungen in den beiden Festlands-Datensätzen, was repräsentiert wird durch die Größe des Kastens und der Position der Endpunkte der Ausreißer.

Allerdings passen einige Modelle (z. B. 6, 9 und 11) viel besser zu den Festlands-Datensätzen als zu den globalen Temperatur-Datensätzen. Dies würde auf Probleme hindeuten mit der Repräsentation der Ozeane in diesen Modellen.

Schlussfolgerungen? Nun, die größte Änderung von Jahr zu Jahr der Temperatur der Erde während der letzten 140 Jahre hat 0,3°C betragen, sowohl für steigende als auch für fallende Temperatur.

Sollten wir also einem Modell vertrauen, das eine doppelt so große Änderung von Jahr zu Jahr zeigt wie beispielsweise GFDL (11)? Welchen Wert hat ein Modell, deren Ergebnisse nur halb so groß sind wie die Beobachtungen, wie GISS (12) und CSIRO (7)?

Meine wesentliche Schlussfolgerung lautet: an irgendeiner Stelle müssen wir den Gedanken der Klimamodelle-Demokratie verwerfen und alle Modelle über Bord werfen, die nicht die Realität abbilden, die nicht einmal ansatzweise die Beobachtungen spiegeln.

Mein letzter Punkt ist ein Seltsamer. Er betrifft die merkwürdige Tatsache, dass sich ein Ensemble (ein origineller Ausdruck für einen Mittelwert) der Klimamodelle im Allgemeinen besser macht als irgendein ausgewähltes Einzelmodell. Ich habe das aus folgendem Grunde verstanden.

Nehmen wir einen Haufen kleiner Kinder an, die noch nicht so gut werfen können. Man zeichnet ein Ziel an einer Scheune, und die Kinder werfen Schlammbälle auf das Ziel.

Was wird nun näher am Zentrum des Zieles liegen – das Mittel aller Würfe der Kinder oder ein speziell ausgewählter individueller Wurf?

Es scheint eindeutig, dass das Mittel aller schlechten Würfe die bessere Wahl ist. Eine Folge davon ist, je mehr Würfe es gibt, desto genauer wird das Mittel wahrscheinlich sein. Also ist dies vielleicht die Rechtfertigung in den Köpfen der IPCC-Leute für die Einbeziehung von Modellen, die die Wirklichkeit gar nicht abbilden … sie wurden mit einbezogen in der Hoffnung, dass sie ein genauso schlechtes Modell auf der anderen Seite ausbalancieren.

ABER – es gibt Probleme bei dieser Annahme. Ein Problem ist, falls alle oder die meisten Fehler in die gleiche Richtung gehen, dann würde das Mittel nicht besser sein als ein Einzelwert-Ergebnis. In meinem Beispiel nehme man an, dass das Ziel sehr hoch auf die Scheune gemalt wurde, und die meisten Kinder treffen einen Bereich darunter. Dann würde das Mittel nicht besser aussehen als irgendein individuell ausgewählter Wurf.

Ein weiteres Problem ist, dass viele Modelle große Teile der Codierung gemeinsam haben, und noch wichtiger, sie teilen eine ganze Reihe theoretischer (und oftmals nicht untersuchter) Annahmen, die hinsichtlich des Klimas stimmen können oder nicht.

Ein tiefer gehendes Problem in diesem Falle ist, dass die verbesserte Genauigkeit nur für die Nachhersage der Modelle gilt … Und sie sind ohnehin schon sorgfältig frisiert worden, um diese Ergebnisse zu zeigen. Keine Frisierung nach Art des „Drehens am Knopf“, sondern wieder und immer wieder evolutionäre Frisierung. Als Folge zeigen sie alle ziemlich gut die Temperaturvariationen der Vergangenheit, und das Mittel ist sogar besser als die Nachhersage … lediglich diese blöde Vorhersage ist immer das Problem.

Oder wie es die Börsianer an den US-Börsen ausdrücken: „Das Verhalten der Vergangenheit ist keine Garantie für zukünftige Erfolge“. Es spielt keine Rolle, wie gut ein individuelles Modell oder eine Modellgruppe die Vergangenheit abbilden kann – das bedeutet absolut nichts hinsichtlich ihrer Fähigkeit, die Zukunft vorherzusagen.

Anmerkungen:

Datenquelle: Die Modell-Temperaturdaten stammen aus einer Studie von Forster, P. M., T. Andrews, P. Good, J. M. Gregory, L. S. Jackson, and M. Zelinka, 2013, Journal of Geophysical Research, 118, 1139–1150 mit dem Titel Evaluating adjusted forcing and model spread for historical and future scenarios in the CMIP5 generation of climate models, dankenswerterweise zur Verfügung gestellt von Piers Forster. Sie steht hier und ist des Lesens wert.

Daten und Codierung: Wie üblich ist mein R-Code ein Gewirr, aber zu was das taugt, steht hier. Die Daten finden sich in einer Excel-Tabelle hier.

Link: http://wattsupwiththat.com/2013/11/21/one-model-one-vote/

Übersetzt von Chris Frey EIKE

Anmerkung des Übersetzers: Ich bitte um Verständnis, dass ich diesem Text inhaltlich manchmal nicht ganz folgen konnte.