Das R. W. Wood-Experiment

Zu Beginn möchte ich ein kurioses Beispiel eines Treibhauseffektes zeigen, nämlich den eines Stahl-Treibhauses. Man stelle sich einen Planeten im Vakuum des Weltalls vor. Ein Überbleibsel nuklearen Materials, das im Erdkern zerfällt, erwärmt den Planeten so weit, dass er eine Strahlung von, sagen wir, 235 W/m² abstrahlt. Abbildung 1 verdeutlicht das.

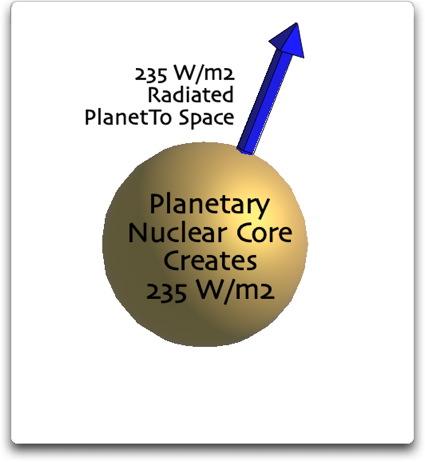
Abbildung 1: Planet im freien Weltraum, erwärmt aus seinem Inneren. Die Zeichnung zeigt die Lage im Gleichgewicht.
Dieser Planet befindet sich im Gleichgewicht. Der natürliche Reaktor im Kern des Planeten erzeugt Energie, die sich an der Oberfläche des Planeten auf 235 W/m² beläuft. Die Strahlungsmenge ist immer gleich, so dass sich dieser Planet weder erwärmt noch abkühlt.
Jetzt stellen wir uns vor, dass wir, ohne sonst irgendetwas zu verändern, einen Stahlmantel um den Planeten legen. Abbildung 2 zeigt diese Situation, wobei eine Seite der Hülle zeitweise entfernt wird, damit man nach innen schauen kann.

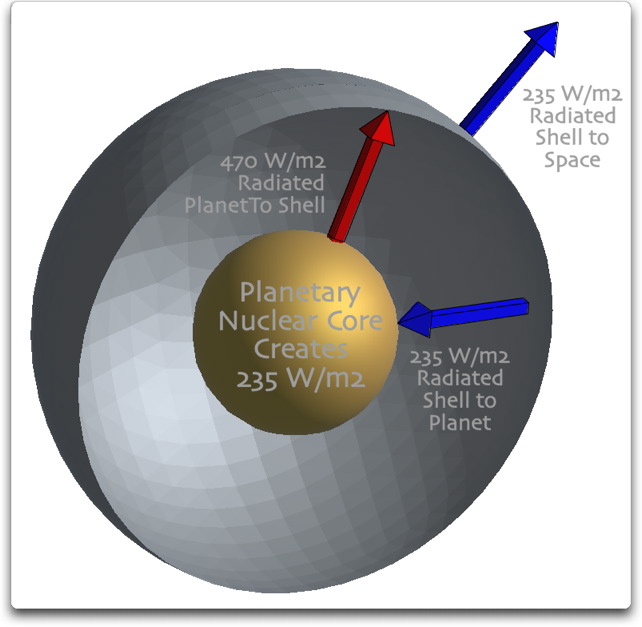
Abbildung 2: Wie in Abbildung 1, aber jetzt mit einer soliden Stahlhülle um den Planeten. Eine Seite der Hülle wurde zeitweise entfernt, um nach innen sehen zu können. Die vertikale Distanz zwischen der Hülle und der Oberfläche des Planeten ist der Anschaulichkeit halber stark übertrieben – in Wirklichkeit haben die Oberfläche und die Hülle* fast die gleiche Oberfläche. (Eine Hülle 10 km über der Erde hat nur eine um 0,3% größere Oberfläche als die Erde).
(Aktualisierung: In den Kommentaren zum Vorschein kommende Missverständnisse glauben, dass ich Klarheit vermissen lasse. Hierzu möchte ich Folgendes sagen: Weil die Differenz der äußeren Oberfläche der Hülle und der Planetenoberfläche nur etwa 0,3%* ausmacht, mache ich die vereinfachende Annahme, dass beide Oberflächen gleich sind. Dies klärt die Lage um großen Teil. Ja, damit kommt ein gewaltiger Fehler von 0,3% in die Berechnungen. Über diesen Fehler haben sich die Kommentatoren lang und breit ausgelassen, als ob er etwas bedeuten würde… Wirklich, Leute, 0,3%? Ich mache auch die vereinfachende Annahme, dass sowohl der Planet als auch die Hülle „Schwarzkörper“ sind, soll heißen, sie absorbieren die gesamte auftreffende Infrarotstrahlung).
[*Vielleicht war der Autor Eschenbach hier nicht so in Form. Im Original steht an dieser Stelle die Zahl 0,03%. Auch hier scheint es sich eindeutig um einen Schreibfehler im Original zu handeln. A. d. Übers.]
Betrachten wir jetzt, was passiert, wenn wir eine Hülle um den Planeten legen. Die Hülle erwärmt sich und beginnt nun ihrerseits zu strahlen… aber sie strahlt nach innen und nach außen die gleiche Menge ab. Die nach innen gerichtete Strahlung erwärmt die Oberfläche des Planeten, bis er mit 470 W/m² strahlt. An diesem Punkt befindet sich das System wieder im Gleichgewicht. Der Planet empfängt 235 W/m² aus seinem Inneren plus 235 W/m² von der Hülle, und strahlt die Gesamtmenge ab, 470 W/m². Die Hülle empfängt 470 W/m² vom Planeten und strahlt die gleiche Menge ab, 470 W/m², zur Hälfte nach innen zum Planeten und zur Hälfte nach außen in den Weltraum. Man beachte auch, dass obwohl die Oberfläche des Planeten jetzt wärmer ist (und 470 W/m² abstrahlt) trotzdem Energie gespart wird. Die gleichen 235 W/m² Energie wie in Abbildung 1 werden in den Weltraum abgestrahlt.
Und das ist alles, was es mit dem Treibhauseffekt auf sich hat. Er erfordert kein CO2 oder eine Atmosphäre, er kann sich aus Stahl einstellen. Es hängt vollständig von der Tatsache ab, dass die Hülle zwei Seiten hat und ein fester Körper nur eine.
Dieses Zaubersystem funktioniert, weil es zwischen dem Planeten und der Hülle ein Vakuum gibt. Als Folge können der Planet und die Hülle sehr unterschiedliche Temperaturen annehmen. Wenn sie das nicht könnten, wenn zum Beispiel die Hülle durch gewaltige Säulen gehalten werden würde, die effektiv die Weiterleitung der Wärme von der Oberfläche zur Hülle gewährleisten würden, würden die beiden immer die gleiche Temperatur aufweisen, und die Temperatur wird von einer Größe sein. Dass das System 235 W/m² abstrahlt. Es gäbe keine unterschiedliche Erwärmung der Oberfläche, und es gäbe keinen Treibhauseffekt.
Ein anderer Weg, die Effizienz des Systems zu verringern, wäre die Einführung einer Atmosphäre. Jedes Watt Energie, das durch die atmosphärische Wärmekonvektion von der Oberfläche zur Hülle verloren geht, reduziert die Strahlungstemperatur der Oberfläche um den gleichen Betrag. Falls die Atmosphäre die Oberflächentemperatur effektiv genug an die Hülle weiterleiten kann, wird die Oberfläche nur wenig wärmer als die Hülle.
Zusammenfassend: Wenn der Treibhauseffekt funktionieren soll, muss die Hülle thermisch von der Oberfläche isoliert sein, so dass die Temperaturen der beiden substantielle Unterschiede annehmen können. Falls die Atmosphäre oder irgendetwas Anderes die Wärme der Oberfläche effektiv zur Hülle transferiert, wird die Temperatur zwischen beiden nur geringe Unterschiede aufweisen.
Und jetzt erinnern wir uns daran, dass ich das Experiment von R. W. Wood betrachten wollte. Hier folgt der Bericht von diesem Experiment vom Autor. Ich habe den experimentellen Aufbau in den Mittelpunkt gerückt.
Bemerkungen zur Treibhaus-Theorie
Professor R. W. Wood
Es scheint der Glaube weit verbreitet, dass die vergleichsweise hohe Temperatur, die in einem der Sonnenstrahlung ausgesetzten Treibhaus erzeugt wird, durch eine Transformation von Wellenlängen erfolgt, das heißt, dass die Wärmestrahlen von der Sonne, die das Glas durchdringen können, auf die Wände des Treibhauses treffen und deren Temperatur erhöhen: Die Wärmeenergie wird von den Wänden in Form viel längerer Wellen rückgestrahlt. Sie können das Glas nicht durchdringen, so dass das Treibhaus als Wärmefalle fungiert.
Ich habe immer meine Zweifel gehabt, ob dieser Vorgang wirklich eine so große Rolle beim Steigen der Temperatur gespielt hat. Viel wahrscheinlicher schien es mir, dass die Rolle des Glases darin bestand zu verhindern, dass die vom Boden innerhalb des Treibhauses erwärmte Luft nach außen entweicht. Wenn wir die Türen des Treibhauses  an einem kalten und windigen Tag öffnen, wird das Zurückhalten der Strahlung viel von seiner Effektivität verlieren. Tatsächlich bin ich der Meinung, dass ein aus Glas bestehendes Treibhaus, das für Wellen jeder möglichen Wellenlänge durchlässig wäre, fast die gleiche, wenn nicht genau die gleiche Temperatur annehmen würde wie in einem Glashaus beobachtet. Die transparente Abschirmung erlaubt es der Sonnenstrahlung, den Boden zu erwärmen, und der Grund wiederum erwärmt dann die Luft, aber nur den begrenzten eingeschlossenen Teil. Im „Freien“ steht der Boden kontinuierlich im Kontakt mit kalter Luft infolge von Konvektiosströmen.
Um das mal zu überprüfen, habe ich zwei Gehäuse aus tiefschwarzem Karton konstruiert, eines abgedeckt mit einer Glasplatte, das andere mit einer Platte Steinsalz [rock-salt] von gleicher Dicke. Der Messfühler eines Thermometers wurde in jedes Gehäuse eingeführt und das Ganze in Baumwolle verpackt mit Ausnahme der transparenten Platten, die frei lagen. Setzte man dies dem Sonnenlicht aus, stieg die Temperatur allmählich bis 65°C, wobei das mit der Salzplatte abgedeckte Gehäuse dem anderen etwas voraus war. Dies ist der Tatsache geschuldet, dass es die längeren Wellen von der Sonne passieren ließ, die durch das Glas zurück gehalten wurden. Um diesen Umstand zu eliminieren, wurde das Sonnenlicht zunächst durch eine Glasplatte geschickt.
Jetzt zeigte sich eine kaum wahrnehmbare Differenz von einem Grad zwischen den Temperaturen in den beiden Gehäusen. Die maximale erreichte Temperatur betrug 55°C. Mit dem, was wir über die Energieverteilung in einem von einem Körper mit 55°C emittierten Strahlungsspektrum wissen, wird klar, dass die Steinsalz-Platte praktisch alles davon hindurch lässt, während die Glasplatte das vollständig verhindert. Dies zeigt uns, dass der Temperaturverlust am Boden durch Strahlung sehr klein ist im Vergleich zum Verlust durch Konvektion. Mit anderen Worten, wir erreichen nur sehr wenig mit dem Umstand, dass die Strahlung gefangen ist.
Ist es daher erforderlich, bei der Ableitung der Temperatur eines Planeten der gefangenen Strahlung Aufmerksamkeit zu zollen, wenn er durch seine Atmosphäre beeinflusst wird? Die Sonnenstrahlen durchdringen die Atmosphäre, erwärmen den Boden, der wiederum die Atmosphäre durch Kontakt erwärmt sowie durch Konvektionsströme. Die empfangene Wärme wird folglich in der Atmosphäre gespeichert und verbleibt dort wegen der sehr geringen Strahlungskraft eines Gases. Es scheint mir sehr zweifelhaft, dass eine Atmosphäre in größerem Umfang durch Absorption von Strahlung von der Oberfläche erwärmt werden kann, selbst unter günstigsten Bedingungen.
Ich sage nicht, dass ich sehr tief in diese Materie eingestiegen bin, und veröffentliche dieses Papier nur, um auf die Tatsache aufmerksam zu machen, dass gefangene Strahlung nur eine sehr kleine Rolle zu spielen scheint in aktuellen Fällen, die uns vertraut sind.
Hier würde meine Interpretation dieses experimentellen Aufbaus stehen:  

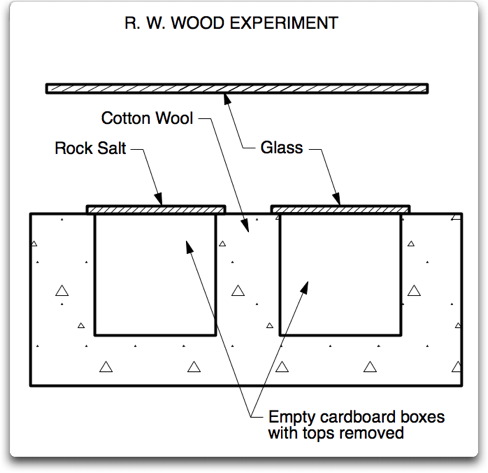
Abbildung 3: Querschnitt durch das Wood-Experiment. Die zwei Kartons sind schwarz gezeichnet. Einer ist mit Glas bedeckt, das Infrarot absorbiert und re-emittiert. Der andere ist abgedeckt mit Steinsalz, welches für Infrarot durchlässig ist. Sie sind in Baumwolle verpackt. Die Thermometer sind nicht gezeigt.
Mit der Diskussion über das Stahl-Treibhaus oben überlasse ich es als eine Übung für interessierte Leser herauszubekommen, warum dies kein stichhaltiger Test der infraroten Gegen-Strahlung im planetarischen Maßstab ist… bitte beachten Sie die Existenz von Luft in den Kartons, die Effizienz des Wärmetransports durch diese Luft von den Kartons zu den Abdeckplatten, das vertikale Temperaturprofil dieser Luft, den Transfer von Energie von der „Oberfläche“ zur „Hülle“ durch die Wände der Schachtel und die relativen Temperaturen der Luft, des Kartons und der transparenten Abdeckung.
Mir scheint allerdings, dass es mit einigen kleinen Änderungen doch ein stichhaltiger Test sein könnte.
Willis Eschenbach
Link: http://wattsupwiththat.com/2013/02/06/the-r-w-wood-experiment/#more-78966
Übersetzt von Chris Frey EIKE