Das Mysterium von Gleichung 8 oder John v. Neumanns Elefant* - EIKE - Europäisches Institut für Klima & Energie

„Warum versuchen Sie alle nicht, unsere WUNDERgleichung zu widerlegen, anstatt Ihre Köpfe gegen die Wand zu schlagen bei dem Versuch, zu beweisen oder zu widerlegen, wer was weiß und zu betonen, dass Sie mit diesem oder jenem Probleme haben? Die Frage lautet, wie wir das haben machen können – keine Frage ist, dass unsere Gleichungen funktionieren – wenn Sie nicht verifiziert haben, dass sie funktionieren, warum haben Sie nicht? (…) Warum denken Sie nicht „hmmmm, N&Z haben uns eine Gleichung gegeben. Wenn man darin den gemessenen Druck eingibt und Tgb wie vorgeschlagen berechnet, erhält man einen berechneten Wert von Ts, der selbst zu gemessenen Werten passt! Sie können die Gleichung nicht widerlegen? Also kochen wir vielleicht irgendwie die richtigen Daten?“
Dies soll der Beweis sein, dass ihre Theorie korrekt ist, und Leute sagen mir immer wieder ‚aber sie haben einen wirklichen Beweis, sie können planetarische Temperaturen vorhersagen, schau mal nach!‘ Außerdem fällt es schwer, eine Einladung nach Art von Dr. Zeller zu ignorieren, also habe ich nachgeschaut.
Abbildung rechts: Es sind nicht diese Gleichungen, nach denen Sie suchen.
Zuerst postulieren sie etwas, das sie den „Atmospheric Thermal Enhancement“- oder „ATE“-Effekt nennen, der die Erde wärmer macht, als sie ohne Atmosphäre wäre.
Der ATE-Effekt” wird durch etwas gemessen, das Nte(Ps) genannt wird, was in ihrer Studie wie folgt definiert und abgeschätzt worden ist.

Darin ist Nte(Ps) ein Maß für den „oberflächennahen Atmospheric Thermal Enhancement“-Effekt.
Nte(Ps) wird definiert als die tatsächliche mittlere Lufttemperatur des Planeten Ts geteilt durch die theoretische „Graukörper“-Temperatur des Planeten Tgb, berechnet aus der totalen solaren Einstrahlung So des Planeten. Nte(Ps) wird abgeschätzt durch Verwendung einer angepassten Funktion des Bodendrucks des Planeten Ts.
Lassen Sie mich das ein wenig vereinfachen. Symbolisch lässt sich der rechte Teil der Gleichung (7) schreiben als
Nte(Ps) = e^(t1 * Ps ^ t2 + t3 * Ps ^ t4) (7Sym)
worin „e“ die Basis des natürlichen Logarithmus‘ und Ps der Bodendruck des Planeten oder Mondes ist. Es gibt vier regelbare Parameter (t1 bis t4), die an die Daten „angepasst“ oder danach ausgerichtet werden. Mit anderen Worten, diese Werte werden wiederholt justiert und ausgerichtet, bis die gewünschte Anpassung erreicht ist. Diese Anpassung kann leicht in Excel mit dem Menüpunkt „Löse…“ vorgenommen werden. Wie zu erwarten war, ist die Anpassung mit vier Parametern und nur acht Datenpunkten ziemlich gut, und ihre Schätzung kommt dem tatsächlichen Wert von Nte(Ps) ziemlich nahe.
Lustigerweise wird das Ergebnis von Gleichung (7) danach in einer anderen angepassten Gleichung verwendet, Nummer (8). Sie lautet:

wobei So die Gesamtsolarstrahlung ist.
Dies ist ihre WUNDERgleichung, von der sie sagen, dass man damit die Oberflächentemperatur von acht verschiedenen Planeten und Monden mit nur zwei Variablen berechnen kann – Pr, der Bodendruck und So, die Gesamtsolarstrahlung. Das ist es, was die Menge der Leute so fasziniert, dass sie mir schreiben, dass es „Beweise“ gibt, dass N&Z recht haben.
Offensichtlich gibt es einen weiteren angepassten Parameter in Gleichung (8), so dass wir sie symbolisch umschreiben können zu:
Ts = t5 * (Solar + adjustment ) ^ 1/4 * Nte(Ps). (8Sym)
Halten wir hier mal einen Moment inne und gestatten uns eine Bemerkung zu Gleichung (8). Die gesamte Sonneneinstrahlung reicht von über 9000 W/m² für den Merkur bis 1,51 W/m² für Triton. Man betrachte Gleichung (8). Wie wird der Faktor 0,0001325 auf jeden dieser Werte vor dem Ziehen der vierten Wurzel im Ergebnis auch nur einen winzigen Unterschied machen? Das ist einfach bizarr. Sie sagen, dass sie es in die Formel einbringen, damit die Formel richtig ist, wenn keine Solarstrahlung vorhanden ist, so dass eine Hintergrundstrahlung von 3 Kelvin herauskommt. Wen kümmert das? Wirklich, es verändert Ts maximal durch ein Tausendstel Grad für Triton. Also wollen wir es für den Moment entfernen, da es keinen praktischen Unterschied und die Dinge nur konfuser macht.
Zurück zu unserer Geschichte. Entfernt man die Anpassung und setzt Gleichung (7) in Gleichung (8) ein, erhält man:
Ts = t5 * Solar^0.25 * e^(t1 * Ps ^ t2 + t3 * Ps ^ t4) (eqn 9)
Das ist faszinierend. Diese Burschen behaupten allen Ernstes, dass sie mit nur acht Datenpunkten und nicht weniger als fünf veränderbaren Parametern die Oberflächentemperatur der acht Planeten berechnen können, nur mit Kenntnis des Bodendrucks und der Sonneneinstrahlung. Und mit so vielen Drehknöpfen bin ich auch sicher, dass sie das tun können. Ich habe es selbst unter Verwendung ihrer Zahlen gemacht. Ich bekomme die gleichen Werte für alle Zahlen von t1 bis t5. Aber das beweist überhaupt nichts.
Ich meine … ich kann nur mit Bewunderung vor der schieren Unverfrorenheit dieser Behauptung stehen. Sie benutzen nur acht Datenpunkte und fünf veränderbare Parameter mit einer speziell gebildeten ad-hoc-Gleichung ohne physikalische Grundlage. Und sie denken nicht im Mindesten daran, wie merkwürdig dies ist.
Ich werde auf diese Frage der Anzahl der Parameter gleich noch einmal zurückkommen, denn obwohl es verblüffend ist, was sie hier gemacht haben, ist es nicht der Höhepunkt der Geschichte. Wir können Gleichung (7) auch auf etwas andere Art in Gleichung (8) einsetzen, indem wir den mittleren Term von Gleichung (7) verwenden. Das ergibt:
Ts = t5 * Solar^0.25 * Ts / Tgb (eqn 10)
Dies bedeutet: wenn wir mit der Kenntnis der Bodentemperatur Ts auf der rechten Seite der Gleichung anfangen, können wir Ts auf der linken Seite berechnen … erschreckend, ich weiß, wer hätte das gedacht. Wir wollen den Rest der Mathematik in Gleichung 10 checken, um zu sehen, warum das herauskommt.
Man kann bei näherem Hinsehen erkennen, dass der erste Teil der rechten Seite von Gleichung (10)
t5 * Solar^0.25
eine andere Form der bekannten Stefan-Boltzmann-Gleichung ist, die den Zusammenhang von Strahlung und Temperatur beschreibt. Diese S-B-Gleichung kann auch geschrieben werden als
T = (Solar / c1) ^ 0.25.
wobei T die Temperatur ist und c1 eine Konstante, die gleich ist der S-B-Konstanten multipliziert mit der Emissivität. Wir können das umschreiben zu
T = 1/(c1^0.25) * Solar^0.25
Setzt man eine andere Konstante c2 = 1/(c1^0.25) ergibt sich die Stefan-Boltzmann-Gleichung zu:
T = c2 * Solar^0.25
Aber das ist genau die Form des ersten Teils der rechten Seite von Gleichung (10). Oder auf den Punkt gebracht, es ist eine Approximation der Graukörper-Temperatur des Planeten Tgb.
Wir können das prüfen, und zwar wenn wir die Emissivität mit 0,9 annehmen, dann beträgt die Konstante c1 5,103E-8, und c2 daher 66. Allerdings reduziert sich dieser Wert durch die Rotation des Planeten. Mit Hilfe der N&Z-Formel in ihrem jüngsten Beitrag ergibt sich ein Wert um 27.
Ihr angepasster Wert ist 25, nicht weit vom tatsächlichen Wert. Also kommt komischerweise heraus, dass sie nichts anderes getan haben als die Stefan-Boltzmann-Konstante mit einer bizarren Methode der Kurvenanpassung abzuschätzen. Und das haben sie gut gemacht. Tatsächlich sogar ziemlich eindrucksvoll, wenn man die Anzahl der Rechenschritte und der involvierten Parameter bedenkt.
Aber da t5  * Solar^0.25 eine Schätzung der Graukörper-Temperatur des Planeten Tgb ist, bedeutet das, dass sich die Gleichung (10) reduziert, und zwar von
Ts = t5 * Solar^0.25 * Ts / Tgb (eqn 10)
zu
Ts = Tgb * Ts / Tgb.
Und schließlich zu
Ts = Ts
TA-DA!
Schlussfolgerung
Lassen Sie mich den zugrunde liegenden Effekt dessen wiederholen, was sie getan haben. Sie betrachteten acht Planeten und Monde.
1.      Sie haben eine Gleichung verwendet
e^(t1 * Ps ^ t2 + t3 * Ps ^ t4)
mit vier freien Parametern für eine Abschätzung von Ts/Tgb, basierend auf dem Bodendruck. Wie man unter der Tatsache erwarten würde, dass es halb so viele freie Parameter wie Datenpunkte gibt und dass sie freie Auswahl haben, irgendeinen davon für ihre Gleichung unbegrenzt auszusuchen, ist das überhaupt kein Problem und kann mit fast jeden Datensatz durchgeführt werden.
2.      Sie haben eine Gleichung verwendet
t5 * Solar^0.25
mit einem freien Parameter, um eine Schätzung von Tgb zusammenzubekommen, die auf der Gesamteinstrahlung des Planeten basiert. Da Tgb unter anderem von der planetarischen Einstrahlung abhängt, gibt es auch hier kein Problem.
3. Sie haben die beiden Schätzungen miteinander multipliziert. Da das Ergebnis eine Schätzung nach der Gleichung Tgb mal einer Schätzung von Ts/Tgb ist, hat das natürlich zur Folge, dass diese Operation Tgb aus der Gleichung hinauswirft.
4. Sie merken an, dass der Rest Ts ist, und erklären das zu einem WUNDER.
Sehen Sie, es wird Ts vorhergesagt, indem man bei Ts anfängt? Überhaupt nicht schwierig, und mit fünf freien Parametern und der Auswahl irgendeiner Gleichung, egal wie nicht-physischer Natur, ist das überhaupt kein WUNDER irgendeiner Art, sondern lediglich ein weiterer Fall einer zügellosen Kurvenanpassung…
Schließlich gibt es eine berühmte Geschichte in der Wissenschaft über diese Art der pseudowissenschaftlichen Verwendung von Parametern und Gleichungen, erzählt von Freeman Dyson:

Wir begannen mit der Berechnung der Mesonen-Protonen-Verteilung unter Verwendung einer Theorie der starken Kräfte, die als pseudoskalare Mesonentheorie bekannt ist. Im Frühjahr 1953 haben wir nach heroischen Bemühungen theoretische Graphen der Mesonen-Protonen-Verteilung geplottet. Wir haben mit Freuden festgestellt, dass unsere berechneten Zahlen ziemlich gut mit den von Fermi gemessenen Zahlen übereinstimmten. Also vereinbarte ich mit Fermi ein Treffen und zeigte ihm unsere Ergebnisse. Stolz fuhr ich im Greyhound-Bus [Greyhound, das führende nationale Busunternehmen in den USA. A. d. Übers.] von Ithaca nach Chicago mit einem Packen unserer theoretischen Graphen, um sie Fermi zu zeigen.
Als ich in Fermis Büro ankam, übergab ich ihm sofort die Graphen, aber er warf kaum einen Blick darauf. Er bat mich, Platz zu nehmen und fragte mich dann freundlich nach der Gesundheit meiner Frau und unseres neugeborenen Sohnes, der heute fünfzig Jahre alt ist. Dann gab er sein Urteil mit einer ruhigen Stimme ohne Höhen und Tiefen ab. Es gibt zwei Möglichkeiten, Berechnungen in theoretischer Physik durchzuführen“, sagte er. „Ein Weg, und zwar der, den ich bevorzuge, besteht darin, ein klares physikalisches Bild des Prozesses vor Augen zu haben, den man berechnet. Der zweite Weg besteht darin, einen präzisen und einen in sich widerspruchsfreien mathematischen Formalismus zu haben. Sie haben keins von beiden“.

Ich war ein wenig geschockt, wagte es aber, ihn zu fragen, warum er die pseudoskalare Mesonentheorie nicht als widerspruchsfreien mathematischen Formalismus sieht. Er erwiderte: „Die Quanten-Elektrodynamik ist eine gute Theorie, weil die Kräfte schwach sind, und wenn der Formalismus mehrdeutig ist, haben wir ein klares physikalisches Bild, das uns leitet. Hinsichtlich der pseudoskalaren Mesonentheorie gibt es kein klares physikalisches Bild, und die Kräfte sind so stark, dass nichts konvergiert. Um Ihre berechneten Ergebnisse zu erlangen mussten Sie frei wählbare Prozeduren [cut-off procedures] einführen, die weder auf solider Physik noch auf solider Mathematik basieren“.
Verzweifelt fragte ich Fermi, ob er nicht wegen der Übereinstimmung zwischen unseren berechneten Zahlen und seinen gemessenen Werten beeindruckt sei. Er erwiderte: „Wie viele frei wählbare Parameter haben Sie für Ihre Berechnungen verwendet?“
Ich dachte einen Moment nach und sagte: „Vier“.
Er sagte: Ich erinnere mich, wie mein Freund Johnny von Neumann zu sagen pflegte, mit vier Parametern kann ich einen Elefanten anpassen, und mit fünf kann ich ihn dazu bringen, mit seinem Rüssel zu wackeln“. Damit war die Unterhaltung beendet. Ich dankte Fermi für seine Zeit und seine Bemühungen und nahm traurig den nächsten Bus zurück nach Ithaca, um den Studenten die schlechten Nachrichten zu überbringen.

Die Gleichung von Nikolov und Zeller enthält fünf Parameter und nur acht Datenpunkte. Wenn ich sagte, dass es kein WUNDER ist, dass sie den Elefanten mit seinem Rüssel wackeln lassen, sondern ein zu erwartendes und triviales Ergebnis ihrer betrügerischen Prozeduren ist, dann habe ich damit alles gesagt.
P.S. – Es gibt natürlich eine technische Bezeichnung für das, was sie getan haben, da es keine neuen Fehler unter der Sonne gibt. Man nennt es „Überanpassung“. Laut Wikipedia: „Überanpassung erfolgt immer dann, wenn ein Modell exzessiv komplex ist, zum Beispiel wenn man zu viele Parameter im Verhältnis zur Anzahl der Beobachtungen hat.“ Fünf Parameter ist ein viel, viel zu großes Verhältnis zu acht Datenpunkten, das ist garantiert überangepasst.
P.P.S. – Ein Problem mit der WUNDERgleichung von N&Z liegt darin, dass sie sie in keiner Weise statistisch getestet haben.
Ein Weg, um zu sehen, ob ihre Anpassung wenigstens vage gültig ist, besteht darin, einige Datenpunkte außen vor zu lassen und die Anpassung noch einmal vorzunehmen. Natürlich ist das mit nur acht Datenpunkten problematisch… aber in jedem Falle kommen die angepassten Parameter radikal unterschiedlich heraus, wenn man das macht, und das weckt viele Zweifel an der Anpassung. Ich ermutige N&Z, das zu tun und über die Ergebnisse zu berichten. Ich werde es tun, aber sie glauben mir nicht, also was soll das?
Ein anderer Weg, ihre Anpassung zu überprüfen, besteht darin, den Datensatz zu halbieren und die eine Hälfte anzupassen und die Ergebnisse mit der anderen Hälfte zu überprüfen. Dies ist so, weil angepasste Gleichungen von der Art, wie sie N&Z verwendet haben, dafür bekannt sind, „außerhalb des Bereichs“ nur sehr bedingt gültig zu sein, das heißt auf Daten, die nicht verwendet wurden, um die Parameter anzupassen. Hat man lediglich acht Datenpunkte und vier Parameter in Gleichung (7), ist dies natürlich wieder problematisch, weil man bei der Teilung des Datensatzes durch zwei genauso viele Parameter wie Datenpunkte hat … nun könnte man denken, dass dies ein Hinweis darauf ist, dass das Verfahren lückenhaft ist, aber was weiß ich schon, ich wurde gestern geboren. In jedem Falle ermutige ich N&Z, auch diesen Test durchzuführen. Meine Ergebnisse eines solchen Tests sagen, dass ihre Anpassung bedeutungslos ist, aber vielleicht sind ja ihre Testergebnisse unterschiedlich.
Aktualisierung Einer der Kommentatoren unten sagte:
Willis – mach weiter – passe einen Elefanten an. Bitte!
Ernsthaft, N&Z zeigen nur mit Hilfe der Algebra, was in Experimenten beobachtet worden ist, nämlich dass das Erwärmen eines Gases in einem geschlossenen Behälter zur Erhöhung sowohl des Drucks als auch der Temperatur führt.
OK, hier kommt meine Nachbildung der Oberflächentemperatur unter Verwendung von nichts weiter als den Daten in der Darstellung von N&Z bzgl. der Eigenschaften planetarischer Körper:

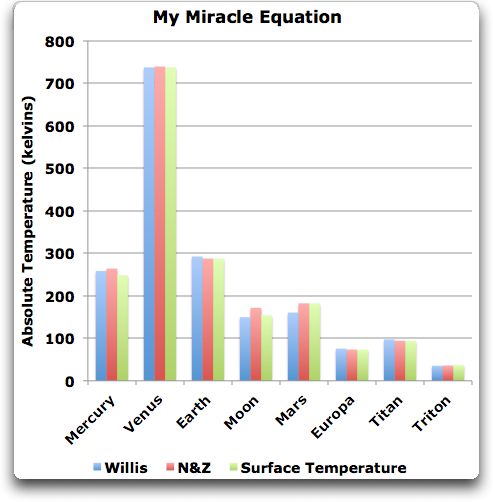
Abbildung 1: Willis’ Nachbildung der Oberflächentemperatur planetarischer Körper.
Meine Gleichung enthält eine Variable mehr und zwei Parameter weniger als die Gleichung von N&Z. Zur Erinnerung, ihre Gleichung lautete:
Ts = 25.3966 * Solar^0.25 * e^(0.233001 * Pressure ^ 0.0651203 + 0.0015393 * Pressure ^ 0.385232)
Meine Gleichung andererseits sieht so aus:
Ts = 25.3966 * Solar^0.25 * e^(0.233001 * Pressure ^ 0.0651203 + 0.0015393 * Pressure ^ 0.385232)
Man beachte, dass ich absolut nicht behaupte, dass die Temperatur durch Dichte und Schwerkraft bestimmt wird. Ich zeige lediglich, dass die Anpassung einiger Punkte mit einigen Variablen und einigen Parametern überhaupt nicht schwierig ist. Es zeigt auch, dass man die Antwort auch ganz ohne Verwendung des Bodendrucks erhalten kann. Und schließlich zeigt es, dass weder meine Nachbildung noch die Nachbildung planetarischer Temperaturen von N&Z auch nur einen Pfifferling wert ist!*
*Im Original steht hier ein Kraftausdruck, den ich lieber nicht direkt übersetzen möchte! A. d. Übers.
2. Aktualisierung Ich habe mir gedacht, dass ich nach den Wundern, die ich mit der Wundergleichung von N&Z angestellt hatte, hier nicht aufhören sollte. Ich sollte schauen, ob ich sie nicht mit ihren eigenen Spielregeln schlagen könnte und ein einfacheres Wunder zu tun. Hier nochmal ihre Gleichung:
Ts = 25.3966 * Solar^0.25 * e^(0.233001 * Pressure ^ 0.0651203 + 0.0015393 * Pressure ^ 0.385232)
Meine vereinfachte Version ihrer Gleichung sieht so aus:
Ts = 25.394 * Solar^0.25 * e^(0.092 * Pressure ^ 0.17)
Komischerweise enthält meine vereinfachte Version einen etwas geringeren RMS-Fehler als die Version von N&Z, also habe ich sie wirklich mit ihren eigenen Spielregeln geschlagen. Meine Gleichung ist nicht nur einfacher, sie ist auch genauer. Es steht ihnen frei, meine vereinfachte Wundergleichung zu benutzen, ohne Honorar. Hier sind die Anpassungen:

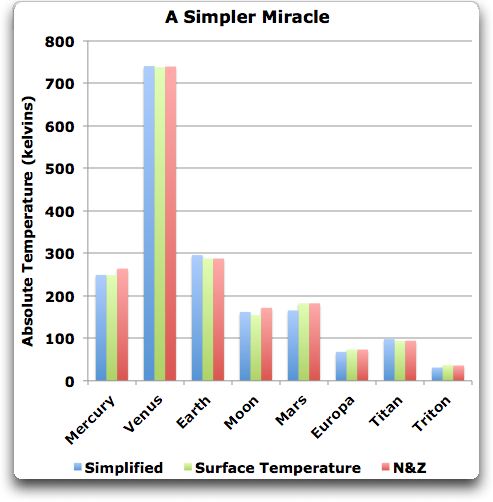
Abbildung 2 Eine einfachere Version der Gleichung 8 von N&Z
Wieder behaupte ich nicht, dass dies die Dinge verbessert. Die bloße Tatsache, dass ich das mit zwei einstellbaren Parametern weniger tun kann (drei anstatt fünf), heißt nicht, dass sie nicht überangepasst ist.
Sowohl die vereinfachte als auch die kompliziertere Form der Gleichungen von N&Z sind nichts weiter als eine Kurvenanpassung. Dies wird durch die Tatsache belegt, dass wir bereits drei einfache und sehr unterschiedliche Gleichungen haben, die die planetarischen Temperaturen bestimmen. Das ist das Gute an einer angepassten Gleichung – wenn man schlau ist, kann man Vieles mit nur etwas finden … aber DAS HEISST NICHT, DASS DER DRUCK DIE TEMPERATUR BESTIMMT .
Zum Beispiel kann ich das gleiche tun, ganz ohne den Druck, sondern stattdessen die Dichte zu verwenden. Diese Gleichung sieht so aus:
Ts = 25.491 * Solar^0.25 * e^(0.603 * Density ^ 0.201)
Und hier sind die Ergebnisse:

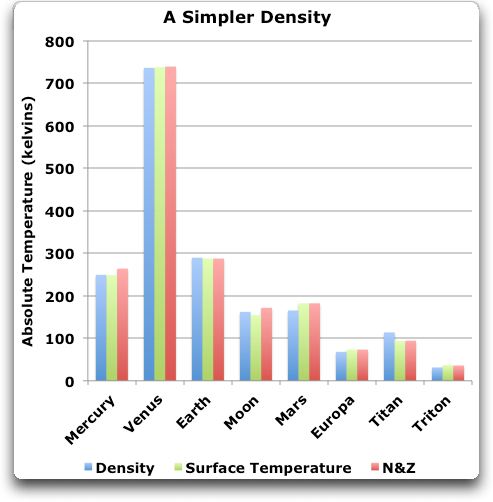
Abbildung 3: Eine Nachbildung der planetarischen Temperaturen unter Verwendung der Dichte anstelle des Drucks.
Heißt das jetzt, dass die planetarische Temperatur wirklich von der Dichte abhängt? Natürlich nicht, das Ganze ist eine Übung zur Anpassung von Kurven.
Link: http://wattsupwiththat.com/2012/01/23/the-mystery-of-equation-8/
Eine ausführliche Erwiderung samt Klarstellung der von W. Eschenbach angegriffenen Autoren finden Sie hier http://tallbloke.wordpress.com/2012/02/09/nikolov-zeller-reply-eschenbach/
Mit Dank an Leser Kieser!
Übersetzt von Chris Frey
* Der berühmte Mathematiker und Erfinder der modernen Computerarchitektur John v. Neumann pflegt zu sagen:"Geben Sie mir vier Variable und ich baue ihnen damit einen Elefanten. Geben Sie mir eine fünfte, dann wackelt er auch noch mit dem Rüssel".