Grundmodell der Erde als Schwarzkörper – Ein ganz schweres Problem

Grundmodell der Erde als Schwarzkörper – Ein ganz schweres Problem

Robert G. Brown, Duke University

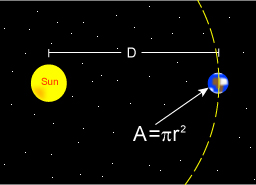
Die Erde hat nur eine Absorptionsfläche, die einer zweidimensionalen Scheibe gleicht, nicht einer Kugeloberfläche.
Eine halbe Nacht lang habe ich im Lern-Halbschlaf über dem Buch von Caballero zum Thema des Strahlungstransfers gebrütet und bin zu zwei Einsichten gekommen:
Erstens: das Grundmodell des Schwarzkörpers (es führt zu T_b = 255K) ist physikalisch ein schreckliches Grundmodell. Es behandelt den Planeten wie einen nicht rotierenden Wärme-Supraleiter ohne Wärmekapazität. Warum das so schrecklich ist? Weil es absolut falsch ist, 33K als Treibhauserwärmung in Bezug auf den Ausgangswert zu setzen. Dieser Ausgangswert ist ein völlig unphysikalischer Ausgangswert.
Zweitens, die 33K bedeuten nichts. Sie werfen Erwärmungs- und Abkühlungseffekte zusammen, absolut nichts mit dem Treibhauseffekt zu tun haben. Mehr dazu später.
Jetzt verstehe ich den Treibhauseffekt viel besser. Ich möchte das jetzt mit meinen eigenen Worten schreiben, weil mir einige von Caballeros Aussagen nicht gefallen, und weil ich denke, dass meine Darstellung einfacher und einleuchtender ist. Ich denke auch daran, sie vielleicht später für einen Modellbausatz zu verwenden, von der Art, wie man sie als Lernspielzeuge kaufen kann.
Fangen wir mit einer nicht rotierenden supraleitenden Kugel an, null Albedo, einheitliche Emissivität, vollständige Schwarzkörper-Strahlung von jedem Punkt der Kugel. Wie hoch ist die Durchschnittstemperatur?
Jetzt behandeln wir die nicht rotierende Kugel als vollständigen Nicht-Leiter, dergestalt, dass sich ein Teil der Oberfläche im Strahlungsgleichgewicht befindet. Wie hoch ist die Durchschnittstemperatur jetzt? Das ist für den Mond ein besseres Modell als das vorhergehende, aber immer noch nicht gut genug. Verbessern wir es!
Wir geben der Oberfläche nun einige thermische Wärme-Kapazität – wir machen sie Wärme-supraleitend, aber nur in vertikaler Richtung und wir nehmen noch eine Masseschale von einiger Dicke an, die eine vernünftige spezifische Wärme hat. Das ändert am vorherigen Ergebnis nichts, solange wir die Kugel nicht rotieren lassen. Oho, nun erhalten wir doch eine andere durchschnittliche (Oberflächen-) Temperatur, diesmal ist es der sphärische Durchschnitt einer Verteilung, die von der sphärischen Breite abhängig ist. Dabei liegt die höchste Temperatur auf der Tagseite nahe beim Äquator kurz nach dem „Mittag“ (verzögert, weil es Zeit braucht, um die Temperatur jedes Blockes zu erhöhen, weil die Einstahlung den Schwarzkörper-Verlust übersteigt, und weil es Zeit zur Abkühlung braucht, weil der Schwarzkörper-Verlust die Strahlung übersteigt, und die Oberfläche hat niemals und nirgends eine konstante Temperatur außer an den Polen (ohne axiale Kippung). Das ist wahrscheinlich ein recht passendes Modell für den Mond, wenn man rückschreitend eine Albedo hinzufügt (damit wird der Anteil der hereinkommenden Energie vermindert, der thermisch ausbalanciert werden muss).
Man kann für jede dieser Veränderungen tatsächlich die exakte parametrische Temperatur-Verteilung errechnen als Funktion des sphärischen Winkels und des Radius, und (durch Integration) die Veränderung berechnen in z. B. der durchschnittlichen Temperatur aufgrund der Annahme eines vollständigen Schwarzkörpers. Beim Übergang von einem supraleitenden, aber im Übrigen perfekt isolierenden (nicht rotierenden), Planeten zu einer lokal detaillierten Balance fällt die nachtseitige Temperatur einfach von ½ der Kugel Ihrer Wahl von 3 K, oder von null K nach sehr langer Zeit (das ist leichter zu idealisieren). Das ist die untere Grenze, unabhängig von Sonneneinstrahlung oder Albedo (in diesem Sinne hier: der Emissivität). Die tagseitige Temperatur hat eine polare Verteilung, wobei ein Pol auf die Sonne blickt, sie variiert nicht-linear mit der Einstrahlung, Albedo, und (wenn Sie sie verändern wollen) mit der Emissivität.
Das vermaledeite T^4 verkompliziert alles! Ich möchte noch nicht einmal das Vorzeichen der Veränderung der Durchschnittstemperatur zuweisen, wenn ich vom ersten Modell zum zweiten übergehe! Jedesmal, wenn ich meine, ein gutes heuristisches Argument für die Aussage von einer niedrigeren Durchschnittstemperatur zu haben, sagt eine innere Stimme – T^4 – bilde lieber das verflixte Integral, weil die Temperatur im Übergangsbereich von der Tagseite her allmählich auf Null gehen muss. und da gibt es eine ganze Menge von geringer Einstrahlung in einem Gebiet (und daher mit niedriger Temperatur), wo die Sonne auf fünf Uhr steht, sogar mit null Albedo und der Emissivität von einer Einheit! Leicht ist nur, den sphärischen Durchschnitt zu erhalten: Wir nehmen einfach den sphärischen Tagseiten-Durchschnitt und teilen durch zwei.
Mit dem Vorzeichen für die rotierende Kugel bin ich auch nicht glücklich, weil es auf vom Zusammenspiel zwischen der erforderlichen Zeit zur Erwärmung der thermischen Last (engl: „thermal ballast“) abhängt, bei gegebener Differenz zwischen Einstrahlung und ausgehender Strahlung und der Rotationsrate. Wenn man mit unendlicher Geschwindigkeit rotieren lässt, ist man wieder bei der supraleitenden Kugel. Wenn man dazwischen rotieren lässt, und – verdammt noch mal – indem man nur die Größe der thermischen Last verändert (die thermische Last bestimmt die Thermisierungszeit), kann man es sogar so einrichten, dass sich eine rasch rotierende Kugel wie die statische nicht-leitende Kugel verhält, oder wie eine langsam rotierende (jeweils zwischen null Wärme-Kapazität und sehr hoher Wärme-Kapazität).
Schlimmer noch, wenn man die Geometrie der axialen Pole verändert (die noch in Bezug auf die Ekliptik als ungekippt angenommen werden). Während zuvor die Tag/Nacht Grenze sich allmählich an T = 0 von der Tagseite annäherte, gilt das nun nur noch an den Polen! Das Integral des polaren Gebietes (bei einem gegebenen Polarwinkel dtheta) ist viel kleiner als das Integral des Äquator-Winkels, und zudem hat man nun auch noch einen darüber verschmierten Satz von festen Temperaturen, die alle Funktionen des Azimut-Winkels phi und des Pol-Winkels theta sind, der verändert sich nicht-linear, wenn man einen der folgenden Parameter ändert: Einstrahlung, Albedo, Emissivität, omega (Winkelgeschwindigkeit der Rotation) und Wärmekapazität der Oberfläche.
Und dabei ist noch nicht einmal eine Atmospäre berücksichtigt! Oder Wasser. Aber wenigstens bis zu diesem Punkt kann man die Temperaturverteilungsrechnung T (theta,phi,alpha,S,epsilon,c) exakt lösen, denke ich.
Darüberhinaus kann man tatsächlich so etwas wie das Wasser recht gut modellieren. Wenn wir uns nun die Erde als mit einer Schicht von Wasser bedeckt anstelle von Luft vorstellen, mit einem Schwarzkörper auf dem Grund und einer dünnen Schicht einer völlig transparenten Frischhaltefolie drauf, um die vermaledeite Verdampfung zu verhindern, dann wird das Wasser zu einem Teil des thermischen Ballasts. Nun braucht es viel viel länger, um die Temperatur einer ein-Meter-dicken Wasserschicht (bei gegebenem Ungleichgewicht zwischen der einfallenden Strahlung) zu erhöhen oder zu vermindern, als die Temperatur im vielleicht oberen Zentimeter eines Felsens, von Dreck oder von Sand. Es dauert viel länger.
Wenn man das alles einigermaßen im Griff zu haben meint, könnte man das Modell mit Meeren und Landmassen füllen (aber immer noch den lateralen Energie-Transfer verbieten, und einen unmittelbaren vertikalen Ausgleich unterstellen). Man könnte dem Wasser die richtige Albedo zuschreiben und es beim Erreichen der richtigen Temperatur gefrieren lassen.
Danach wird es aber wirklich schwer.
Jetzt muss nämlich eine Atmosphäre dazukommen. Auch das noch!
Die Meere müssen Konvektionsfähigkeit erhalten, Dichte und unterschiedliche Tiefen. Und das alles auf einer rotierenden Kugel, wo alles was nach oben geht (Luftmassen) gegen die Erddrehung (relativ zur Oberfläche) abgelenkt wird, wo alles, was herunterkommt, in Richtung der Erddrehung angelenkt wird, was nach Norden geht auf der Nordhalbkugel in Drehrichtung abgelenkt wird (es wird schneller), was nach Süden geht, gegen die Drehrichtung abgelenkt wird, als Funktion von Winkel, Geschwindigkeit und Drehgeschwindigkeit. Verdammte Coriolis-Kraft, sie lenkt die Küstenartillerie ab, usw. Und jetzt erwärmen wir mal dieses verdammte Ding differentiell so, dass überall und über alle Entfernungen Turbulenzen vorkommen, für die wir kaum noch die einfachste Symmetrie für das differentielle Erwärmen haben. So ungefähr, wenn wir ein fünfjähriges Kind Farbe auf die Kugel spritzen lassen, um anzuzeigen, wo Landmassen und Ozeane sind, oder wir hätten ihm auch Spielzeuglastwagen geben und es im sphärischen Sandkasten spielen lassen können, bis eine schöne unregelmäßige Oberfläche entstanden wäre. Und diese Oberfläche hätten wir mit Wasser auffüllen können, bis die Oberfläche ungefähr zu 70 % unter Wasser gestanden hätte.
O weh! Mein armer Kopf raucht!
Wohlgemerkt – Wir haben immer noch keinen Treibhauseffekt dabei! Nur eine Heuristik für die Abkühlung durch Abstrahlung in einem idealen Zustand, der ist ganz wörtlich genommen destilliert; in Temperatur und Höhe aufgebrochen, noch ohne die Präsenz von CO2. Wolken. Luft verteilt sich mit nicht-trivialer kurzer Wellenlänge über den Querschnitt. Energietransfer satt!
Bevor wir uns nun mit dem CO2 auseinandersetzen, müssen wir die Quantenmechanik und das Inzidenzspektrum berücksichtigen, dazu auf die bislang ignorierten Details des Erdbodens, der Luft und des Wassers blicken. Für die Luft brauchen wir einen Temperatur-Gradienten, der sich mit der Feuchtigkeit, der Albedo, der Bodentemperatur verändert, usw. … Die Luftmoleküle üben einen Rückstoß aus, wenn sie die einfallenden Photonen verteilen, und wenn es eine Kollision mit einem anderen Luftmolekül im rechten Zeitintervall gibt, werden sie beide einen Teil oder die gesamte Energie absorbieren und die Luft erwärmen, anstatt sie elastisch zu verteilen. Ein Molekül kann auch eine Wellenlänge absorbieren und eine Kaskade von Photonen mit einer anderen Wellenlänge emittieren (abhängig von seinem Spektrum).
Und zum Schluss müssen die Treibhausgase dazukommen, vor allem CO2, (Wasser ist schon drin). Sie bewirken eine Zunahme der ausgehenden Strahlung von der (wärmeren) Oberfläche in einigen Bändern und transferieren etwas davon auf das CO2, wo sie eingefangen bleibt, bis sie zur Spitze der CO2-Säule diffundiert ist, von wo sie mit kühlerer Temperatur emittiert wird. Die gesamte hinausgehende Kraft wird auf diese Weise aufgespalten, dabei wird das vermaledeite Schwarzkörperspektrum so moduliert, dass verschiedene Frequenzen verschiedene Wirktemperaturen haben, lokal moduliert – von nahezu allem. Temperaturgradient, Feuchtigkeitsgehalt. Wolken. Massentransport von Wärme nach oben oder unten qua Konvektion! Massentransport von Wärme nach oben oder unten qua eingefangener Strahlung in Teilen des Spektrums. Und bitte nicht die Umgehungen vergessen! Alles fließt jetzt, Wind und Verdampfung sind gekoppelt, die Zeitdauer für den Temperaturausgleich des Meeres erstreckt sich nun von „im gleichen Maß wie die Rotationsperiode“ für flache Meere bis zu tausend oder mehr Jahren. Der Ozean ist niemals im ausgeglichenen Zustand, er zieht immer an den Oberflächentemperaturen in die eine oder andere Richtung mit nennenswerter thermischer Last, die Wärme wird nicht für einen Tag, sondern für eine Woche, einen Monat, ein Jahr, eine Dekade, ein Jahrhundert, ein Jahrtausend gespeichert.
Jawohl, eine verdammt harte Nuß! Wer auch immer so etwas „gesichertes Wissen“ (settled science) nennt, muss wirklich nicht mehr ganz bei Trost sein.
Wohlgemerkt: ich habe noch nicht den solaren Magnetismus oder ernsthaftere Modulationen der Sonneneinstrahlung einbezogen, noch nicht die Neigung der Erdachse, die noch einmal alles verändert, weil damit die Zeitskalen an den Polen jährliche werden, Nord- und Südpol sind überhaupt nicht gleich. Man beachte die enormen Unterschiede ihrer thermischen Last und den ozeanischen und atmosphärischen Wärmetransport!
Eine harte Nuß. Vielleicht nehme ich sie mir einmal zum Knacken vor, wenn ich Zeit habe, wenigstens für die ersten wenigen Schritte zu Anfang. Ich möchte zumindest eine bessere Vorstellung von der Richtung der ersten kleinen Schritte gewinnen zum Bau eines Spielzeug-Modells für die Durchschnittstemperatur. (Der Begriff „Durchschnittstemperatur“ meint hier etwas Bestimmtes, nämlich bevor das System chaotisch gemacht wird).
Dr. Robert Brown
Der Aufsatz führte auf WUWT zu einer Diskussion mit derzeit über 430 Beiträgen, die wegen des Umfangs leider nicht mehr übersetzt werden können. Wer sich für die Diskussion interessiert, möge die Beiträge und das Original hier lesen.
Übersetzung: Helmut Jäger, EIKE