Frau Luna ist eine kühle Dame

Welche Auswirkungen haben Temperaturwechsel auf die Durchschnittstemperatur eines Planeten? Warum ist der Mond so viel kälter als erwartet? Die Albedo (Reflektivität) des Mondes ist geringer als die der Erde. Man kann den Unterschied in der Albedo in Fig. 1 sehen. Auf der Erde gibt es viele Stellen, die von Wolken, Schnee oder Eis weiß sind. Der Mond aber ist vorwiegend grau. Daher  beträgt die irdische Albedo ungefähr 0,30, die des Mondes nur 0,11. Der Mond müsste also mehr Energie absorbieren als die Erde, und die Temperatur der Mondoberfläche müsste knapp unter dem Gefrierpunkt von Wasser liegen. So ist es aber nicht. Der Mond ist viel kälter.

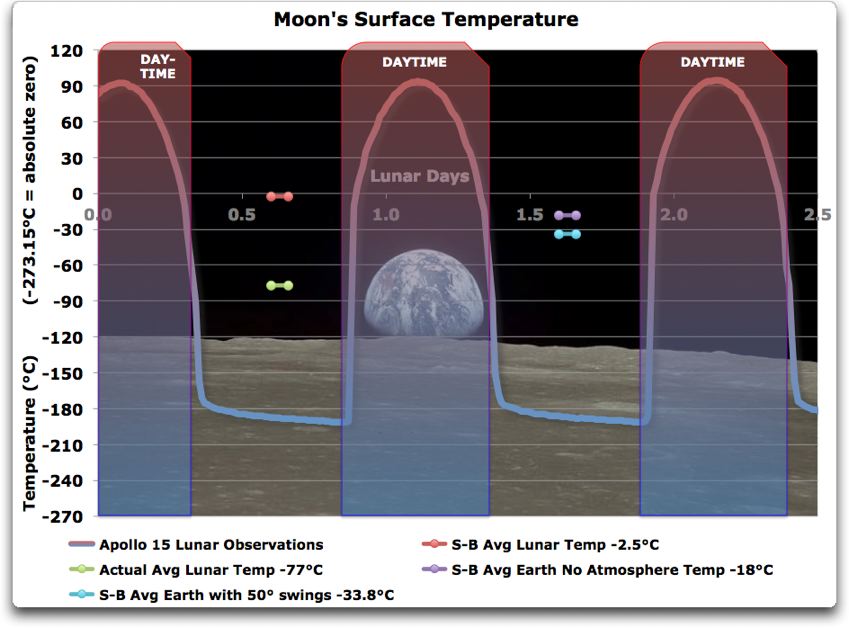
Fig. 1. Beobachtungen Oberflächentemperatur des Mondes von der Apollo15-Mission. Die roten und gelb-grünen kurzen waagerechten Linien links zeigen die theoretischen (rot) und die tatsächlichen (gelb-grün) durchschnittlichen Mondtemperaturen. Die violetten und blauen horizontalen LInien rechts zeigen die theoretische Stefan-Boltzmann-Temperatur der Erde ohne Atmosphäre (violett), und (in hellblau) eine Näherung, um wieviel die Erdtemperatur durch einem ± 50°C Temperaturwechsel vermindert würde infolge der Erdumdrehung. Die Sonnenuntergangstemperatur-Fluktuationen sind aus Gründen der Klarheit der Darstellung ausgelassen. (Daten-Quelle hier)

Wie die Erde empfängt die Mondoberfläche gemittelt etwa 342 Watt/Quadratmeter (W/m2) Sonnenenergie. Wie befinden uns ja im gleichen Abstand von der Sonne. Die Erde reflektiert 30% davon zurück in den Weltraum (Albedo 0,30) und behält etwa 240 W/m2. Der Mond mit seiner geringeren Albedo reflektiert weniger und absorbiert mehr Energie, etwa 304 W/m2.
Und weil der Mond im thermalen Gleichgewicht ist, muss er den gleichen Betrag abstrahlen, wie er von der Sonne erhält, ~ 304 W/m2.
Da gibt es die “Stefan-Boltzmann-Gleichung” (kurz S-B Gleichung, oder einfach S-B), die die Temperatur (in Kelvin) zur thermalen Abstrahlung in Beziehung setzt (in Watt/Quadratmeter). Sie besagt, dass die Abstrahlung proportional zur vierten Potenz der Temperatur ist.
Unter der Voraussetzung, dass der Mond etwa 304 W/m2 Energie in den Weltraum abstrahlt, um die hereinkommende Energie auszubalancieren, beträgt die der S-B Gleichung entsprechende Schwarzkörper-Mondtemperatur etwa 0,5 °C. Das wird auf Fig. 1 durch die kurze horizontale rote Linie dargestellt. Daraus ergäbe sich, dass die Mondtemperatur theoretisch knapp unter dem Gefrierpunkt läge.
Aber die gemessene tatsächliche Durchschnittstemperatur der Mondoberfläche wie in Fig. 1 gezeigt, beträgt minus 77 °C, weit unter dem Gefrierpunkt, wie die kurze waagerechte gelb-grüne Linie zeigt.
Was ist da los? Heißt das, dass die S-B Gleichung falsch ist, oder dass sie auf dem Mond nicht gilt?
Die Lösung des Rätsels ist, dass die Durchschnittstemperatur keine Rolle spielt. Was zählt, ist die Durchschnittsabstrahlung von 304 W/m2. Das ist ein absolutes Muss, das von der Thermodynamik gefordert wird – die durchschnittliche Abstrahlung des Mondes muss gleich der von der Sonne empfangenen Einstrahlung sein: 304 W/m2.
Strahlung ist proportional zur vierten Potenz der Temperatur.  Das bedeutet: Wenn die Temperatur hoch ist, gibt es viel mehr Strahlung, bei Temperaturverminderung ist die Strahlungsverminderung nicht genau so groß. Wenn es also Temperaturwechsel gibt, führen sie zu höherer Energieabstrahlung an der Oberfläche. Als Ergebnis der höheren Energieabstrahlung kühlt sich die Oberflächentemperatur ab. In einer Gleichgewichtssituation wie auf dem Mond, wo der Betrag der abgestrahlten Energie fest ist, reduzieren Temperaturwechsel immer die durchschnittliche Oberflächentemperatur.
Wenn man, wie in Fig. 1 oben, zuerst die nacheinander gemessenen Mondoberflächentemperaturen in die entsprechenden Mengen von Strahlung umrechnet und für diese dann den Durchschnitt bildet, beträgt dieser Durchschnitt 313 W/m2. Das ist nur ein kleiner Unterschied zu den 304 W/m2, die wir aus der ursprünglichen Kalkulation zum einfallenden Sonnenlicht und zur Mond-Albedo haben. Und während diese präzise Berechnung einigermaßen stimmig ist (unter der Voraussetzung, dass unsere Daten von einer einzigen Stelle auf dem Mond stammen), erklärt sie auch die große Differenz zwischen der vereinfachenden Theorie und den tatsächlichen Beobachtungen.
Es besteht also kein Widerspruch zwischen der lunaren Temperatur und der S-B-Kalkulation. Die durchschnittliche Temperatur wird von den Temperaturwechseln vermindert, während die durchschnittliche Strahlung gleichbleibt. Das tatsächliche lunare Temperaturmuster ist eines von vielen möglichen Temperaturveränderungen, die zur selben durchschnittlichen Variation von 304 W/m2 führen können.
Eines ist aber merkwürdig. Die niedrige lunare Durchschnittstemperatur ist die Folge des Ausmaßes der Temperaturwechsel. Je größer der Temperaturumschwung ist, desto niedriger ist die durchschnittliche Temperatur. Wenn der Mond sich schneller drehen würde, wären die Umschwünge kleiner und die Durchschnittstemperatur wärmer. Wenn es keine Temperaturwechsel gäbe und die Mondoberfläche überall gleichmäßig erwärmt würde, läge die Mondtemperatur kaum unter dem Gefrierpunkt. Alles, was die Temperaturveränderungen vermindert, würde die Durchschnittstemperatur auf dem Mond erhöhen.
Die Umschwünge wären kleiner, wenn der Mond eine Atmosphäre hätte, selbst wenn diese Atmosphäre keine Treibhausgase enthielte und für Infrarot völlig durchlässig wäre. Ein Effekt einer  völlig durchlässigen Atmosphäre ist, dass sie Energie von warm nach kalt transportiert. Das würde natürlich die Temperaturwechsel und Differenzen vermindern und schließlich den Mond leicht erwärmen.
Auf eine weitere Art und Weise würde eine sogar völlig durchlässige und treibhausgasfreie Atmosphäre den Mond erwärmen, indem sie dem System thermische Masse zufügte. Weil die Atmosphäre erwärmt und gekühlt werden muss, wie auch die Oberfläche, wird das auch die Temperaturwechsel vermindern und wiederum die Oberfläche leicht erwärmen. Es wäre keine große thermische Masse, und nur der geringste Teil hätte eine signifikante tägliche Temperaturfluktuation. Schließlich beträgt die spezifische Wärme der Atmosphäre nur etwa ein Viertel im Vergleich zu Wasser. Aus dieser Kombination von Faktoren würde nur ein nur ganz geringer Effekt folgen.
Hier möchte ich nun aufhören zugunsten eines wichtigen Arguments: Diese letzten beiden Phänomene bedeuten, dass ein Mond mit einer perfekt transparenten treibhausgasfreien Atmosphäre wärmer wäre als ein Mond ohne eine derartige Atmosphäre. Eine transparente Atmosphäre könnte die Mondtemperatur niemals über die S-B-Schwarzkörpertemperatur von einem halben Grad Celsius heben.
Der Beweis ist trivial einfach und kann durch die Behauptung des Gegenteils erbracht werden:
Die Behauptung würde lauten: Eine perfekt transparente Atmosphäre könnte die durchschnittliche Temperatur des Mondes über die Schwarzkörpertemperatur heben, das ist die Temperatur, bei welcher 304 W/m2 emittiert würden.
Doch nur die Mondoberfläche könnte in diesem System Energie emittieren, weil die Atmosphäre transparent wäre und keine Treibhausgase enthielte. Wenn also die Oberfläche wärmer als die theoretische S-B-Temperatur wäre, würde die Oberfläche mehr als 304 W/m2 in den Weltraum emittieren und nur 304 W/m2 aufnehmen.
Das wäre dann ein „perpetuum mobile“.  Q.E.D. (Quod Erat Demonstrandum – Was zu beweisen war)
Während also eine perfekt transparente Atmosphäre ohne Treibhausgase das Ausmaß der Abkühlung vermindern kann, die von Temperaturwechseln herrühren, kann sie nur die Abkühlung abschwächen. Es gibt eine physikalische Grenze, um wieviel sie den Planeten erwärmen kann. Im äußersten Falle, wenn alle Temperaturwechsel völlig ausgeglichen würden, können wir nur die S-B-Temperatur bekommen, nicht mehr. Das bedeutet, dass zum Beispiel eine transparente Atmosphäre nicht für die derzeitige Erdtemperatur ursächlich sein kann, weil die Erdtemperatur deutlich über der theoretischen S-B-Temperatur von ~ -18 °C liegt.
An diesem Punkt angelangt frage ich mich, wie die Temperaturwechsel der Erde ohne Atmosphäre aussähen. Unter Beachtung der derzeitigen Albedo zeigen grundlegende Kalkulationen, dass eine Erde ohne Atmosphäre eine Schwarzkörpertemperatur von 240 W/m2 ≈ -18°C hätte. Um wieviel würde aber die Erdumdrehung den Planeten abkühlen?
Unglücklicherweise rotiert der Mond so langsam, dass er kein gutes Analogon zur Erde darstellt. Aber es gibt ein Stück lunarer Information, das wir benutzen können. Das ist, wie rasch der Mond nach Sonnenuntergang auskühlt. Für diesen Fall wären Mond und Erde ohne Atmosphäre grob gleichsetzbar, beide würden ganz einfach in den Weltraum abstrahlen. Beim lunaren Sonnenuntergang beträgt die Mondoberflächentemperatur etwa -60° C (Fig. 1). Über die folgenden 30 Stunden fällt sie stetig mit einer Rate von etwa 4° C pro Stunde bis auf etwa –180 °C. Von da an kühlt sie sich leicht während der nächsten zwei Wochen ab, weil die Abstrahlung so gering ist. So beträgt die kälteste Temperatur der Mondoberfläche etwa –191 °C, und dabei strahlt sie sage und schreibe zweieinhalb Watt pro Quadratmeter ab … daher ist die Strahlungsabkühlung sehr, sehr langsam.
Also … machen wir diese Rechnung für die Erde! Wir können grob abschätzen, dass sich die Erde etwa mit der lunaren Rate von 4 °C pro Stunde über die Dauer von 12 Stunden abkühlt. Dabei würde die Temperatur um etwa 50 °C fallen. Tagsüber würde sich sich durchschnittlich auch so erwärmen. Wir könnten uns also vorstellen, dass die Temperaturwechsel auf einer Erde ohne Atmosphäre eine Größenordnung von ± 50°C hätten. (Aber die tatsächlichen Temperaturwechsel auf der Erde sind viel kleiner, im maximum etwa ± 20-25 °C, und das in Wüstengebieten.)
Wie stark würde ein ±50 °C Umschwung eine Erde ohne Atmosphäre abkühlen?
Dank eines Stückchens schöner Mathematik von Dr. Robert Brown (http://wattsupwiththat.com/2012/01/06/what-we-dont-know-etwa-Energie-flow/) wissen wir, dass die Strahlung um 1 + 6 * (dT/T)^2 variiert, unter der Voraussetzung, dass dT die Größe des Temperaturwechsels um den Durchschnitt nach oben und unten ist, wobei T die Mitteltemperatur des Temperaturwechsels ist. Mit ein bisschen mehr Mathematik (im Appendix) würde dies bedeuten, dass die durchschnittliche Temperatur bei – 33 °C läge, wenn der Betrag der eingestrahlten Sonnenenergie 240 W/m2 (≈ -18°C) wäre und die Temperaturwechsel ± 50°C betrügen. Einiges der Erwärmung von dieser kühlen Temperatur käme aus der Atmosphäre selbst und Einiges aus dem Treibhaus-Effekt.
Dabei zeigt sich wieder etwas Interessantes. Ich hatte immer angenommen, dass die Erwärmung von den Treibhausgasen nur auf die direkten Erwärmungseffekte der Strahlung zurückzuführen wären.  Aber ein Charakteristikum der Treibhausgasstrahlung (niedergehende Langwellenstrahlung, auch DLR genannt) ist, dass sie sowohl tagsüber wie nachts wirkt, vom Äquator bis zu den Polen. Aber es gibt sicher Unterschiede in der Strahlung in Abhängigkeit vom Ort und von der Zeit. Insgesamt aber ist einer der großen Effekte der Treibhausgasstrahlung, dass sie die Temperaturwechsel stark reduziert, weil sie zusätzliche Energie zu Zeiten und an Orten bereitstellt, wo die Sonnenenergie nicht da oder stark vermindert ist.
Das bedeutet, dass der Treibhauseffekt die Erde auf zwei Wegen erwärmt – direkt, und indirekt durch die Verminderung der Temperaturwechsel. Das ist neu für mich und es erinnert mich daran, dass das Beste beim Studium des Klimas ist, dass man immer noch etwas dazulernen kann.
Zum Schluss:  Jedes weitere Grad Erwärmung kostet immer mehr Energie im Zuge der Erwärmung der irdischen Systemerwärmung.
Ein Teil dieses Effekts ist darauf zurückzuführen, dass die kühlende Abstrahlung mit der vierten Potenz der Temperatur steigt. Ein Teil des Effekts ist aber auch darauf zurückzuführen, dass Murphys Gesetz immer gilt, dergestalt, dass wie bei Ihrem Automotor parasitäre Verluste (Verluste von fühlbarer und latenter Wärme von der Oberfläche) rascher zunehmen als die Antriebsenergie. Und schließlich gibt es einen Anzahl von homöostatischen Mechanismen im natürlichen Klimasystem, die die Erde vor Überhitzung schützen.
Derartige thermostatische Mechanismen sind z. B.:
• Der zeitliche Verlauf und die Anzahl der Tropengewitter.
• Die Tatsache, dass Wolken die Erde im Winter wärmen und im Sommer abkühlen.
• Der Energieübertragungmechanismus der Ozeane durch El Niño/La Niña.
Diese Mechanismen wirken mit weiteren zusammen, um das Gesamtsystem um etwa ein halbes Grad pro Jahrhundert stabil zu halten. Das bedeutet eine Temperaturvariation von weniger als 0.2%. Man beachte, da steht nicht: weniger als zwei Prozent. Die globale Durchschnittstemperatur hat sich im Verlauf eines Jahrhunderts weniger als um zwei Zehntel eines Prozents verändert, das ist eine erstaunliche Stabilität in einem so unglaublich komplexen System, das von so flüchtigen Ingredienzen wie den Wolken und dem Wasserdampf gesteuert wird. Ich kann diese Temperaturstabilität nur der Existenz von solchen multiplen, einander sich überschneidenden und redundanten thermostatischen Mechanismen zuschreiben.
Als Ergebnis, nachdem der Treibhaus-Effekt die schwere Arbeit des Anhebens der Erdtemperatur auf die gegenwärtige Höhe geleistet hat, werden die Auswirkungen der Veränderungen der Antriebe bei der gegenwärtigen Gleichgewichtslage durch Veränderungen der Albedo und der Wolkenzusammensetzung und die Umschwünge im Energiedurchsatz ausbalanciert mit sehr geringen Veränderungen der Temperatur.
Doch am schönsten ist der Vollmond heute abend, jung und kristallklar. Ich gehe jetzt hinaus und schaue ihn an.

Oh schöner voller Mond,
der du nachts den Teich umkreist,
immerdar und ewig gleich.

Matsuo Basho, 1644-1694

w.
Original mit Anhang auf WUWT
Übersetzung: Helmut Jäger, EIKE