Eine kontroverse Diskussion über Schwarzkörperstrahlung und eine Erde ohne Treibhausgase

Bild rechts via Wikipedia
Da ich nicht sicher bin, wie die „charakteristische Emissionstemperatur der Erde“ definiert ist, kann ich den behaupteten Wert von 255 K nicht in Abrede stellen. Allerdings kann ich – und das ist auch so – mit der Behauptung, dass 255 K „die Temperatur ist, die an der Erdoberfläche beim Fehlen jeglicher Treibhausgase herrscht“ nicht übereinstimmen.
Wenn man die Temperaturdifferenz an der Erdoberfläche „mit und ohne alle Treibhausgase“ berechnet, müssen 1) zwei Temperaturen (A und B) gemessen/abgeschätzt werden und 2) die Differenz beider Werte berechnet werden. Die erste Temperatur A ist die auf der Erde gemessene Temperatur unter Gegenwart einer Atmosphäre, die sowohl Treibhausgase, als auch Nicht-Treibhausgase beinhaltet. Die zweite Temperatur B ist die Temperatur auf der Erde unter Gegenwart einer Atmosphäre ausschließlich ohne Treibhausgase – d. h. eine Atmosphäre, die Gase ohne Treibhauswirkung enthält, aber der Treibhausgase fehlen.
Für Temperaturwert A benutzt fast jeder eine „gemessene Mitteltemperatur“ an der Erdoberfläche. Obwohl der Algorithmus zur Berechnung eines „gemessenen Mittels“ diskussionswürdig ist, möchte ich für diesen Artikel alle solche Diskussionen beiseite schieben und den Wert von 288 K als Wert für Temperatur A akzeptieren (die Temperatur an der Erdoberfläche in Gegenwart einer Atmosphäre, die sowohl Treibhausgase als auch Gase ohne Treibhauswirkung enthält.)
Folglich bleibt nur, einen Weg zu finden, Temperatur B zu messen/abzuschätzen. B können wir nicht direkt messen, weil wir die Treibhausgase aus der Erdatmosphäre nicht entfernen können. Dies bedeutet, dass wir einen Algorithmus (ein Modell) benutzen müssen, um B abzuschätzen. Ich glaube, dass der zur Berechnung der 255-K-Temperatur allgemein benutzte Algorithmus NICHT mit einem Modell „der Temperatur an der Erdoberfläche in einer Atmosphäre, die ausschließlich Gase ohne Treibhauswirkung enthält“ korrespondiert. Wie aus meiner Beschreibung hervorgehen wird (unten), ist dieser Algorithmus, wenn überhaupt, eher repräsentativ für den Modellwert „in einer Atmosphäre, die sowohl Treibhausgase als auch Gase ohne Treibhauswirkung enthält“ als für ein Modell der „Temperatur auf der Erde in einer Atmosphäre, die ausschließlich Gase ohne Treibhauswirkung enthält.“
Wenn ich Recht habe, ist die Verwendung des Wertes 255 K bei der Berechnung der Temperaturdifferenz mit und ohne Treibhausgase ungültig.
Obwohl es viele Algorithmen gibt, die potentiell zu einem Wert von 255 K als Schätzwert für B führen, präsentiere ich hier den Algorithmus, von dem ich annehme, dass er der am meisten Benutzte ist, und diskutiere, warum dieser Algorithmus NICHT „die Temperatur in Gegenwart einer Atmosphäre ist, der Treibhausgase völlig fehlen“. Ich glaube, dass der unten beschriebene Algorithmus die fundamentale Gleichung des Strahlungstransports im System Erde/Sonne repräsentiert, und zwar unter den Annahmen a) einer Absorptionsalbedo der Erde von 0,3 und b) einer irdischen Emissivität von 1.
 (1) Die effektive Temperatur” der Sonne (d. h. die Temperatur eines sonnengroßen sphärischen Schwarzkörpers, für den die ausgestrahlte elektromagnetische Leistung (a) repräsentativ ist für die gesamte abgestrahlte Leistung und (b) für den die Spektraldichte der Strahlung [power spectral density] ähnlich der der Sonne ist) beträgt etwa 5778 K.
(2) Für einen sphärischen Schwarzkörper mit einem Radius von 6,96×10^8 Metern (dem geschätzten Radius der Sonne) bei einer gleichförmigen Oberflächentemperatur von 5778 K (a) beträgt die gesamte abgestrahlte Kraft etwa 3,85 x 10^26 Watt, (b) beträgt die Spektraldichte in einer Entfernung von 1,5 x 10^11 Metern vom Zentrum des Schwarzkörpers (die ungefähre Entfernung des Erdkerns vom Sonnenkern) etwa 1367 Watt pro m².
(3) Falls sich das Zentrum einer Sphäre mit einem Radius von 6,44 x 10^6 Metern (dem ungefähren Erdradius) in einer Entfernung von 1,5 x 10^11 Metern vom Zentrum der Sonne entfernt befindet, beträgt das „effektive Absorptionsgebiet“ dieser Sphäre hinsichtlich der Schwarzkörperstrahlung von der Sonne in guter Näherung 1,3 x 10^14 m²; und darum liegt die Auswirkung der solaren Strahlung auf das effektive Absorptionsgebiet der Sphäre mit einem Radius von 6,44 x 10^6 Metern etwa bei 1,78 x 10^17 Watt (1,3 x 10^14 m² mal 1367 Watt pro m²).
(4) falls die Sphäre mit dem Radius 6,44 x 10^6 Metern elektromagnetische Energie mit einer „effektiven Absorptionsalbedo“ von 0,3 absorbiert, dann beträgt die von der Sphäre absorbierte solare Energie 1,25 x 10^17 Watt (1,78 x 10^17 Watt mal (1-0,3)).
(5) Ein sphärischer Schwarzkörper (d. h. ein sphärischer Körper, dessen Oberfläche wie ein solcher mit einer Emissivität von 1 strahlt) mit einem Radius von 6,44 x 10^6 Metern und einer Temperatur von 254,87 K (hierbei gerundet zu 255 K) wird Energie mit einer geschätzten Rate von 1,25 x 10^17 Watt abstrahlen.
(6) Falls die Oberflächentemperatur der Sphäre unabhängig von der Richtung der einfallenden Strahlung zu jeder Zeit überall gleich ist, dann besitzt die Sphäre die Eigenschaft eines perfekten thermischen Leitvermögens. Folglich ist (a) ein inaktiver (ohne eigene thermale Energiequelle) sphärischer Körper mit einem perfekten thermischen Leitvermögen und einem Radius von 6,44 x 10^6 Metern und einer gleichmäßigen Temperatur von 255 K, dessen Zentrum sich 1,5 x 10^11 Meter vom Zentrum eines aktiven sphärischen Schwarzkörpers (mit einer eigenen internen thermischen Energiequelle) und einem Radius von 6,96 x 10^8 Metern und einer gleichmäßigen Temperatur von 5778 K entfernt befindet, und (b) der sphärische Körper mit den o. g. Eigenschaften (i) elektromagnetische Energie mit einer effektiven Absorptionsalbedo von 0,3 absorbiert und (ii) elektromagnetische Energie mit einer Emissivität von 1 abstrahlt, dann wird sich der inaktive sphärische Körper im Strahlungsgleichgewicht mit dem aktiven sphärischen Schwarzkörper mit einer Temperatur von 5778 K befinden. Wenn der Terminus „inaktiver sphärischer Körper mit perfektem thermischen Leitvermögen und einem Radius von 6,44 x 10^6 Metern“ durch das Wort „Erde“ ersetzt wird und der Terminus „aktiver sphärischer Schwarzkörper mit einem Radius von 6,96 x 10^8 Metern und einer gleichmäßigen Oberflächentemperatur von 5778 K“ durch das Wort „Sonne“ ersetzt wird, kann man daraus folgern: Falls (a) eine „Erde“ mit einer Temperatur von 255 K 1,5 x 10^11 Meter von der „Sonne“ entfernt liegt und (b) die „Erde“ (i) elektromagnetische Energie absorbiert mit einer effektiven Absorptionsalbedo von 0,3 und (ii) Energie mit einer Emissivität bei 1 abstrahlt, dann befindet sich die „Erde“ im Strahlungsgleichgewicht mit der „Sonne“. Unter diesen Bedingungen wird die Temperatur der „Erde“ im Strahlungsgleichgewicht mit der „Sonne“ 255 K betragen.
Dies vervollständigt den Algorithmus, von dem ich glaube, dass er gemeinhin benutzt wird, um einen Wert von 255 K als „charakteristische Emissionstemperatur der Erde“ zu erhalten und folglich benutzt wird, um die 33 K Temperaturdifferenz zu berechnen.
Selbst wenn man die Tatsachen ignoriert, dass (1) es nicht korrekt ist, die „mittlere Temperatur“ zu benutzen, wenn man den Strahlungsenergieverlust von einer Oberfläche berechnet, und dass (2) in Gegenwart einer Atmosphäre (a) die Schwarzkörperstrahlungsgleichung nicht angewendet werden kann und (b) die Schwarzkörperstrahlung von der Erdoberfläche nicht der einzige Mechanismus für den Energieverlust der Erde in Richtung Weltall ist (die Atmosphäre selbst ohne Treibhausgase wird erwärmt durch Ableitung von der Erdoberfläche, und Ableitung sowie Konvektion zusammen führen dazu, dass die thermische Energie in der gesamten Atmosphäre verteilt wird, und die so erwärmte Atmosphäre wird ebenfalls Energie in den Weltraum abstrahlen), besteht das Problem in der Verwendung des oben berechneten Temperaturwertes von 255 K bei der Berechnung der Erdtemperatur zwischen einer Atmosphäre mit und ohne Treibhausgase darin, dass die effektive Absorptionsalbedo der Erde von 0,3 zur Erzeugung der Temperatur von 255 K teilweise (hauptsächlich?) auf die Wolken in der Atmosphäre zurückzuführen ist, und atmosphärische Wolken bilden sich aus Wasserdampf, einem Treibhausgas.
Folglich basiert die effektive Absorptionsalbedo von 0,3 auf der Gegenwart eines Treibhausgases – Wasserdampf. Es ist unlogisch, eine Differenz zwischen zwei Temperaturwerten zu berechnen, deren Werte beide auf der Gegenwart eines Treibhausgases basieren und dann zu behaupten, dass die Temperaturdifferenz zwischen einer Atmosphäre mit und ohne Treibhausgase auftritt. Ohne Wasserdampf gäbe es keinerlei Wolken, wie wir sie kennen. Ohne Wolken dürfte die effektive Absorptionsalbedo der Erde wahrscheinlich nicht 0,3 betragen, und folglich wird die Temperatur der Erde ohne das Treibhausgas Wasserdampf wahrscheinlich ein anderer sein als 255 K. Folglich ist der Wert von 255 K als „charakteristische Emissionstemperatur der Erde“, wie er sich unter Verwendung des oben beschriebenen Algorithmus’ ergibt, NICHT relevant bei der Diskussion über die Temperaturdifferenz auf der Erde bei einer Atmosphäre mit und ohne Treibhausgase. Nur falls 0,3 die effektive Absorptionsalbedo der Erde in Gegenwart einer Atmosphäre ganz ohne Treibhausgase ist, ist die Behauptung gestattet, dass die Anwesenheit von Treibhausgasen die Temperatur auf der Erde um 33 K zunehmen lässt.
Weil die Wolken einen signifikanten Teil der einfallenden Sonnenstrahlung reflektieren, glaube ich, dass die effektive Absorptionsalbedo der Erde ohne Wasserdampf weniger als 0,3 ist. Falls das stimmt, dann wird von einer Erde, deren Atmosphäre frei von Treibhausgasen ist, mehr Sonnenenergie absorbiert als von einer Erde, deren Atmosphäre Wolken aus dem Treibhausgas Wasserdampf enthält. Dies impliziert bei Fehlen von Wasserdampf eine höhere Temperatur auf der Erde als die „charakteristische Emissionstemperatur der Erde von 255 K“.
Für eine effektive Absorptionsalbedo von 0, wird die Temperatur der Erde im Strahlungsgleichgewicht mit der Sonne etwa 278,64 K betragen (hiernach gerundet zu 279 K). Wenn dieser Wert als Temperatur der Erde in Gegenwart einer Atmosphäre ohne Treibhausgase verwendet wird, kann man daraus schließen, dass die Gegenwart von Treibhausgasen zu einer Erwärmung von etwa 9 K führt (288K minus 279 K).
Zusammengefasst: Unter Verwendung der vereinfachten Argumente, von denen ich glaube, dass sie auch benutzt werden, um bei den 33 K Temperaturdifferenz anzukommen (d.h. unter Voraussetzung einer Erde mit einer perfekten Wärmeleitfähigkeit, Schwarzkörperstrahlung der Erde, Graukörperabsorption der Erde mit einer effektiven Absorptionsalbedo zwischen 0 und 0,3 und unter Ignorieren der atmosphärischen Strahlung in Richtung Weltraum bei einer Erdatmosphäre ohne Treibhausgase), schließe ich, dass die Gegenwart von Treibhausgasen in der Erdatmosphäre die Temperatur zwischen 9 und 33 K steigen lässt. Folglich glaube ich, dass die Behauptung, die Gegenwart von Treibhausgasen führe zu einer Temperaturzunahme auf der Erde von 33 K auf einem Argument basiert, das wenig Relevanz hinsichtlich der Temperatur der Erde beim Fehlen von Treibhausgasen in der Atmosphäre besitzt; und dass dieser Wert folglich im besten Falle irreführend und im schlimmsten Falle falsch ist.
Reed Coray
den Originalartikel finden Sie hier
lesen Sie auch den Beitrag von Michael Krüger zum selben Thema auf Science Sceptical "Die Wohlfühltemperatur der Erde"

Update zu den Kräften zwischen Sonne und Erde

Paul L. Vaughan, M.Sc.
Die Amplitude der zonalen Winde auf der Erde wird vom solaren Zyklus gesteuert. Hier folgt ein knappes Update auf Basis der jüngsten Daten:
LOD’ = Rate der Änderung der Tageslänge


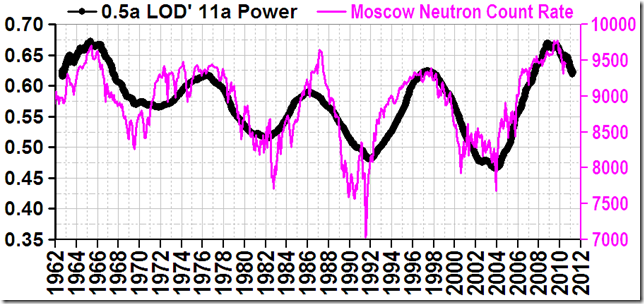
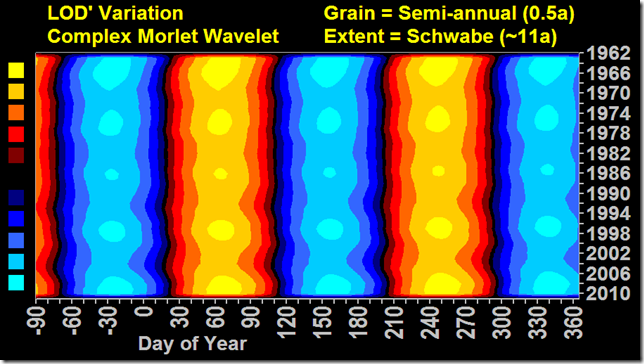
Quelle der Bilder:
ftp://ftp.iers.org/products/eop/long-term/c04_08/iau2000/eopc04_08_IAU2000.62-now ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/COSMIC_RAYS/STATION_DATA/Monthly_data/moscow.tab
Link hierzu: http://wattsupwiththat.com/2011/12/25/solar-terrestrial-power-update/
Übersetzt von Chris Frey für EIKE
Bemerkung des Übersetzers: Dieser Text war wieder ein „harter Knochen“ zum Übersetzen. Einmal waren viele Sätze mehrfach verschachtelt, zum Anderen haben manche Passagen die Grenzen meiner Fachkenntnisse überschritten. Für wohlwollende Korrekturvorschläge der von mir übersetzten Fachausdrücke wäre ich dankbar. Wer nur solche Vorschläge machen will, ohne den Artikel selbst zu kommentieren, sollte über den Menüpunkt Kontakt direkt an das EIKE schreiben. Danke!