Teil I Globaltemperatur grob fehlerhaft! Neue begutachtete Studien enthüllen: Fehler deutlich größer als gesamte Änderung im letzten Jahrhundert.
Jetzt hat Pat Frank ein unerschrockener und erfahrener Experimental-Wissenschaftler der alten Schule, die Rechenmethoden für die Globaltemperaturberechnung des IPCC auf messtechnische, mathematische und logische Richtigkeit überprüft. Sein Ergebnis, das in zwei begutachteten Aufsätzen veröffentlicht wurde: die mittlere Temperatur der Erde kann nicht genauer als mit ± 1 °C bestimmt werden. Damit ist jede Änderung, die daraus abgeleitet wird, statistisch von Null nicht zu unterscheiden. Jede Zuordnung von Ursachen für nicht von Null unterscheidbare Änderungen ist daher Spekulation.
Seit vielen Jahrzehnten wird uns von den Medien mitgeteilt, dass eine globale Mitteltemperatur existiere und diese sich in nie dagewesene Höhen aufgeschwungen hätte. Die Ursache dafür, so wird ständig wiederholt, läge beim Menschen.
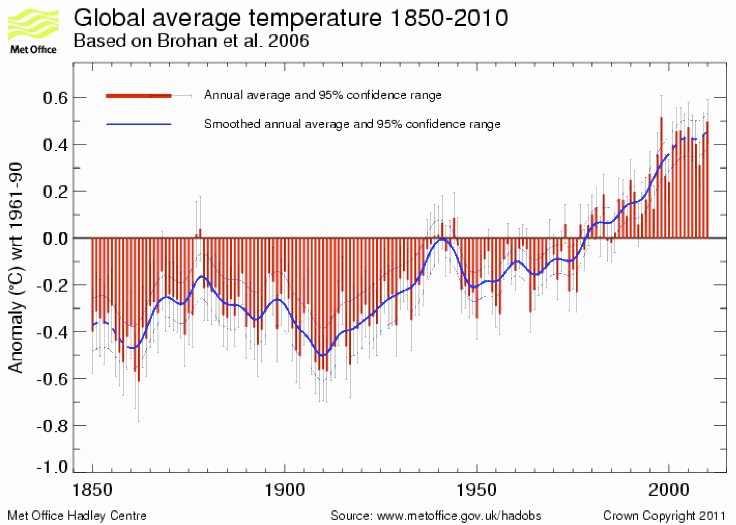
Abbildung 1 Die blaue mittlere Trendlinie zeigt globale Mitteltemperatur wie sie vom britischen Met-Office [0]von 1850 bis Ende 2010 im Internet zu Verfügung gestellt wird. Ihr überlagert ist die nach Brohan et al ermittelte Unsicherheit von ± 0,1 K. Die Referenzzeit ist hier 1961-1990
Belegt wird diese Behauptung – inzwischen umfassend mit der Wirkung eines vermuteten anthropogenen Treibhauseffektes begründet- und zum schlichten "Klimawandel[1]" verkürzt, mittels diverser wissenschaftlicher Studien. Eindrucksvoll zusammengefasst in den Abschätzungs-Berichten der IPCC Reports zum Klimawandel. Widerspruch dagegen wird immer häufiger als Häresie, ja als Gotteslästerung angesehen. Es herrsche doch Konsens unter 97 % der Wissenschaftler, so wird jedenfalls behauptet (Details dazu hier).
Doch jedem, der auf der Oberschule Physikunterricht genossen hat und ihn nicht vorzeitig abwählte, müssen die veröffentlichen globalen Temperaturkurven irgendwie merkwürdig vorkommen. Man wird sich erinnern, wie umständlich es schon in der Schule war, auch nur in zwei dicht benachbarten Räumen, deren Temperatur auf 1/2 ° C genau zu bestimmen. Allenfalls gelang eine Momentaufnahme und nur an diesem Ort. Wie kann es dann gelingen, eine Temperatur der ganzen Welt auf ± 1/10 ° C und dazu noch über 150 Jahre, genau zu bestimmen?
Die Antwort ist: Das kann man nur, wenn man diverse Fehler, die unvermeidbar auftreten, von denen man viele zwar vermuten kann, deren genauen Wert und Verlauf man jedoch nur grob schätzen könnte, glatt unter den Tisch fallen lässt. Das ist bei der Berechnung der globalen Mitteltemperatur und ihres Trendverlaufes nachweislich geschehen. Dies ist gelegentlich auf böse Absicht zurückzuführen (wie die ClimateGate Emails zu beweisen scheinen), häufiger auf blinden Ehrgeiz, unbedingt das gewünschte Ergebnis zu erzielen, aber am allerhäufigsten wohl auf ein mangelhaftes Verständnis der Grundlagen der Fehlertheorie, des altehrwürdigen und gut bekannten, aber sehr speziellen Zweiges der mathematischen Statistik. Die besagen nämlich, dass sich auch mit noch so ausgefeilten statistischen Methoden aus höchst ungenauen und unvollständigen Daten keine präzisen Messergebnisse herleiten lassen. Doch genau das wird mit erheblichem Aufwand versucht. Aber anders lässt sich dieses merkwürdige, selten offiziell angezweifeltes und falsches Ergebnis der offiziellen Klimainstitute nicht erklären.
Pat Frank, ein promovierter Physiko-Chemiker [2], der sich in seiner langen beruflichen und wissenschaftlichen Laufbahn viel mit Spektralmessungen und deren Auswertung beschäftigte, hat jetzt -im bekannt aufmüpfigen Wissenschaftsjournal "Energy & Environment"- nacheinander zwei begutachtete Fachbeiträge[3] [4] veröffentlicht, die Aufsehen erregen müssen. Zugegeben, in der Fachöffentlichkeit haben die Zeitschriften "Nature" und "Science" trotz diverser grober Fehler, gerade in Sachen Klimaforschung, noch einen höheren Stellenwert als "Energy & Environment". Aber saubere wissenschaftliche Redaktions- und Begutachtungsarbeit wird auch dieser Zeitschrift, selbst von Gegnern, bescheinigt.
Die erste Arbeit von Pat Frank erschien im Winter 2010. Ihr Titel: „Uncertainty in the global average surface air temperature index: representative lower limit“
In der Zusammenfassung zu diesem Aufsatz schreibt Frank:
Zitat: Die Messfühler (Sensor)-Messunsicherheit wurde nie umfassend in früheren Aufsätzen zur mittleren globalen bodennahen Lufttemperatur berücksichtigt. Der geschätzte durchschnittliche ± 0,2 °C Stations-Fehler wurde fälschlicherweise als zufällig beurteilt, während der systematische Fehler, bestimmt durch unkontrollierte Variablen, immer vernachlässigt wurde. Der systematische Fehler bei den Messungen von drei ideal gelegenen und (ideal) gewarteten Temperatursensoren wurde hier berechnet. In Kombination mit dem mit ± 0,2 ° C allgemein berichteten Durchschnitts Stations-Fehler, wurde eine repräsentative untere Grenz-Unsicherheit von ± 0,46 °C für alle globalen jährlichen bodennahen Lufttemperatur Anomalien gefunden. Diese ± 0,46 ° C zeigt, dass der Trend der globalen bodennahen Lufttemperatur Anomalie von 1880 bis 2000 statistisch nicht von 0 ° C zu unterscheiden ist, und stellt somit eine untere Grenze der Kalibrierunsicherheit für Klimamodelle und für jeden mögliche physikalisch vertretbare Proxy-Rekonstruktion der Paläo-Temperatur dar. Die Geschwindigkeit und das Ausmaß der Erwärmung des 20. Jahrhunderts sind somit unbekannt, und Vermutungen von einer beispiellosen Entwicklung der globalen Lufttemperatur im 20. Jahrhundert sind somit nicht nachhaltig (begründbar). Zitatende
Das ist eine klare Ansage. Sie stellt, wenn sie sich denn als richtig erweisen sollte, und daran besteht kein vernünftiger Zweifel, der offiziellen Klimaforschung ein denkbar schlechtes Zeugnis aus. Doch um die Brisanz dieser Aussage wirklich nachvollziehen zu können, sollte man sich ein wenig mit der Fehlertheorie beschäftigen. Danach unterscheidet man drei Arten von Fehlern: Zufällige Fehler, systematische Fehler und grobe Fehler.
Zufällige Fehler
Zufällige Fehler entstehen immer bei jeder Messung und sind unvermeidbar. Beispielsweise zeigt jedes noch so genaue Thermometer unter der Bedingung, dass bei jeder Messung immer dieselbe Temperatur gemessen wird, zum Beispiel in kochendem Wasser, immer einen leicht anderen Wert als genau 100 °C an. Schreibt man die ermittelten Werte auf und misst genügend oft, dann streuen die Messungen um den „wahren“ Messwert häufig gleichverteilt herum. Bei Mittelung gleichen sie sich bei genügend großer Anzahl von Messungen aus. Wobei sie dadurch gekennzeichnet sind, dass sie völlig zufällig auftreten und deshalb durch Mittelung minimiert werden können. Ihr Mittelwert tendiert also im Idealfall gegen Null. Diese Fehler nennt Frank in seinem Papier „Rausch-Fehler“. (Noise Errors)
Systematische Fehler.
Jedes Messinstrument, aber auch jeder Messprozess, erzeugt bei der Messung zudem systematische Fehler. Diese haben unter sonst gleichen Bedingungen und immer auf denselben Fehler bezogen immer dasselbe Vorzeichen und immer denselben Wert. Sind sie bekannt, dann können sie mittels einer Korrekturrechnung ausgeglichen werden. Ein gutes Beispiel für einen systematischen Fehler ist eine Uhr (ein Zeitmesser), die immer 5 Minuten vorgeht. Diese 5 Minuten kann man von der angezeigten Zeit einfach abziehen, um auf die genaue Zeit zu kommen. Sind sie aber nicht bekannt, dann gibt es keinen Weg sie zu vermeiden. Sie müssen als Fehlergröße oder Unsicherheit der Messung angegeben werden.
Grobe Fehler
Das sind Fehler, die einfach grob falsche Ergebnisse liefern. Z.B. wenn eine Messstation deshalb keine Ergebnisse anzeigt, weil sie nicht abgelesen wurde. Oder wenn bei der Übertragung ein grober Zahlendreher passierte, oder wenn eine Temperaturmessung in einem Eisblock statt am Kochherd gemacht wurden. Grobe Fehler lassen sich nicht ausgleichen, die Messergebnisse müssen verworfen werden
Pat Franks 1. Aufsatz konzentriert sich nun auf die zufälligen und sensoreigenen systematischen Fehler.
Er zeigt mit einiger Mathematik, dass sich bei den meteorologischen Messungen, die zufälligen Fehler (oder Messunsicherheiten) komplizierter verhalten, als es die einfache Fehlertheorie, die bisher auf sie angewendet wurde, bescheibt.
In der Klimatologie wird der Aufsatz von Brohan et. al 2006[5] als maßgeblich für die Bestimmung der Unsicherheitsbandbreite des mittleren globalen Temperaturtrends angesehen. Sie geben in ihrer Arbeit (und beziehen sich dabei auf Folland et. al 2001) diesen (dort „station error“ genannten) gesamten mittleren Stations-Fehler (genauer; die Standardabweichung 1σ) mit ±0,2 °C an. D.h. sie unterstellen (von Folland 2001 übernommen) , dass 68,3 % (Vertrauensbereich [6]) der Messwerte jeder Station im Bereich von ± 0,2 °C um den wahren Wert gleichverteilt herum liegt. Nun fallen bei der täglichen Bestimmung von z.B. Max. und Min. Temperatur täglich zwei Messungen an. Im Monat sind das 60.
Unterstellt man nun, dass dieser mittlere Stations-Fehler (Messfehler oder Messunsicherheit) von ± 0,2 ° C für jeden Messwert, wie im oben genannten Standardaufsatz zur Bestimmung des gesamten zufälligen Fehlers der globalen Mitteltemperatur geschehen, auftritt, dann lautet das Ergebnis für den gesamten Fehler des Monatsmittels – jedoch nur bei immer derselben Temperatur unter sonst gleichen Bedingungen gemessen-
![]() °C
°C
Diese einfache Formel ist heute schon geschichtsträchtig und damit legendär, denn sie erlaubt, aus ungenauen Messwerten, sehr genaue Trends herzuleiten. Sie begründete damit den Glauben einer ganzen Generation von Klimaforschern an präzise globale Temperaturtrends, weil sie die schöne Eigenschaft hat, aus ungenauen, nicht mehr änderbaren historischen Messwerten, sehr genaue Rechenwerte zu erzeugen. Genau das, was die Klimatologen für die Berechnung einer hinreichend genauen globalen Mitteltemperatur brauchten.
Sie hat aber leider einen großen Nachteil! Sie ist für klimatologische Temperaturmessungen so nicht einsetzbar, weil sie für Messarten angewendet wird, für die sie nicht entwickelt wurde. Es werden damit Messfehler nicht berücksichtigt, die zwar unvermeidbar vorkommen, aber mit dieser Formel unterdrückt werden.
Pat Franks Verdienst ist es nun, diese Formel an die reale Welt angepasst zu haben. Er hat dazu ihre Bedeutung zur Klärung ihrer Schwächen einfach wörtlich genommen, wie es auch Brohan et al selber erklären. Wenn die Fehler jeder einzelnen Messung so sind, wie dort angenommen, dann müsste jeden Tag 2 x dieselbe Temperatur τi [7]
gemessen werden. Mit ![]()
Weil das offensichtlich nicht so ist, die Temperaturen ja definitiv verschieden sind, muss zusätzlich dieser Temperatur τi eine – „Wetterrauschen“ wi genannte Komponente- addiert, welche die maximale Tagestemperatur von der konstanten Temperatur, aber auch der minimalen Tagestemperatur, und auch von den Messdaten der Folgetage, unterscheidet. Aber, und das ist die Bedingung, der Mittelwert all dieser Wetterrauschwerte wi, muss – weil zufällig á la Brohan et. al – gegen Null tendieren. Des Weiteren unterliegt jede Messung dem eigenen Signalrauschen des Sensors. Dieser Signal-Rauschfehler muss ebenfalls zur konstanten Temperatur τi addiert werden. Nur dann lässt sich der Fehler nach der bekannten Formel ![]() gegen Null ausmitteln. N ist dabei die Zahl der Messungen.
gegen Null ausmitteln. N ist dabei die Zahl der Messungen.
Doch diese Annahme ist offensichtlich physikalischer Unsinn. Die Max-Temperatur eines Tages ist stark von den Strahlungs- und Wetterbedingungen tagsüber abhängig, die Min-Temperatur von ganz anderen Strahlungs- und Wetterbedingungen des nachts. Keine davon ist konstant. Doch lässt diese Betrachtungsweise zu, dass mittels der dann folgenden Betrachtungen, ein systematischer Fehler abgeleitet werden kann, der zwangsläufig bei realen verschiedenen Messwerten der Max- und Min- Temperatur auftritt und nicht unterschritten werden kann.
Frank beginnt damit die drei theoretisch möglichen Fälle zu unterscheiden, bei denen man erfolgreich Rauschverminderungstechniken, oder hier Verminderungstechniken zufälliger Fehler[8], ansetzen kann und wann nicht. Er beschreibt dazu 3 Klassen von Zuständen, die anfangs ideal einfach, später komplizierter, die Möglichkeiten darstellen zufällige und systematische Instrumenten-Fehler zu klassifizieren und sie mathematisch zu definieren. Die Klasse 3 ist bei ihm die, welche der Wirklichkeit am nächsten kommt. Hier wird davon ausgegangen, dass die jeweiligen Messwerte immer verschieden sind und auch ihre Rauschanteile verschieden sind. Zudem sind alle voneinander statistisch unabhängig. Das ist bei den Wetter-Temperaturmessungen immer der Fall.
Auf die oben erwähnte -zu einfache- Formel bezogen, bedeutet das, dass sie wegen der sich ständig ändernden Messwerte, die täglich, jeweils nur 1 x (ein Max. Wert und ein Min. Wert) um einen zufälligen nicht normalverteilten Fehler ±σ und zusätzlich einen systematischen Fehleranteil s ergänzt werden muss. Hundertmal denselben Wert zu messen und dann daraus evtl. normalverteilte zufällige Fehler zu bestimmen, ist eben nicht dasselbe, als 100 verschiedene einzelne Messwerte mit verschiedenen zufälligen Fehlern zusammen zu fassen und dann ihren Gesamt-Fehler zu bestimmen.
Hatte man vorher 100 Messwerte um den einen „wahren“ Wert herum, so hat man nun 100 Messwerte, die von 100 „wahren“, aber verschiedenen, Werten leichter oder stärker abweichen können.
Unter der Überschrift: Zweck der Studie schreibt er
Zitat
Diese Studie entwickelt eine untere Grenze für die Unsicherheit, die in die Temperatur-Aufzeichnungen -bei den geschätzten zufälligen und systematischen Fehlern- eingeführt werden muss und die Feld-Auflösung der terrestrischen Sensoren beeinflusst.
Eine grundlegende Signalmittelung wird eingeführt und dann verwendet, um die Bedeutung der geschätzten ± 0,2 C durchschnittlichen Unsicherheit aufzuklären, die bei terrestrischen Temperaturmessungen seitens Folland, et al. [12] geschätzt wurde. Eine Schätzung der Rausch-Unsicherheit für jede bestimmte jährliche Temperatur-Anomalie wird dann entwickelt. Im Anschluss daran werden die unteren Grenzen der systematischen Fehler bei drei Temperatursensoren anhand zuvor berichteter idealer Feldstudien [13] ermittelt.
Schließlich wird die durchschnittliche (Mess)-Rausch-Unsicherheit und die untere Grenze des systematischen (Instrumenten-) Fehlers in einem Maximum-Minimum Temperatur Mess-System (MMTS)-Sensor in eine gesamt untere Grenze der Unsicherheit für eine jährliche Anomalie, bezogen auf ein 30-Jahres-Mittel kombiniert. Die Wirkung dieser unteren Grenz-Unsicherheit auf den globalen Durchschnitt der bodennahen Lufttemperatur Anomalie Zeitreihe wird beschrieben. Die Studie endet mit einer Zusammenfassung und einer kurzen Diskussion über den Nutzen des instrumentellen bodennahen Lufttemperatur Aufzeichnung als einme Validierungs- Ziel in Klima-Studien.
Zitat Ende (Klammerbegriffe vom Autor ergänzt)
Mittels diesen neuen Ansatzes vermag Pat Frank die untere Grenze bei Max-Min Temperaturmessungen unter idealen Bedingungen zu definieren. Dazu setzt er die sehr gründliche Bestimmung von Temperatur – Sensorfehlern von Lin and Hubbard [9] ein und benutzt diese – fast idealen Sensoren- als untere erreichbare Grenze.
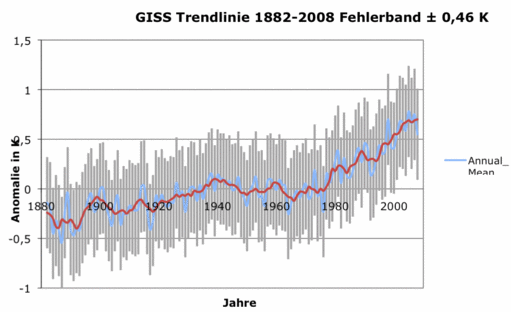
Abbildung 2 Die rote mittlere Trendlinie zeigt globale Mitteltemperatur wie sie vom amerikanischen Goddard Institute of Space Sciences (http://data.giss.nasa.gov/gistemp/graphs/) GISS von 1880 bis Ende 2008 im Internet zu Verfügung gestellt wird. Ihr überlagert ist die minmale Unsicherheit nach Frank in Höhe von ± 0,46 K. Die Referenzzeit ist hier 1951-1980
Im Abschnitt: 3.2. „An empirical approach to temperature uncertainty“ beschreibt er die Vorgehensweise und leitet darin die beiden Komponenten der nichtvermeidbaren Restfehler ab. Sie errechnen sich bei Verwendung modernster Technologien für die Temperatursensoren, zudem bei bester Wartung und mit sauberster Kalibrierung mit
![]()
Da im wirklichen Leben, wie besonders die Arbeit von Antony Watts mit seinem Surface Station Project gezeigt, die Verhältnisse bei den terrestrischen Messstationen wesentlich schlechter sind und waren, kann Frank mit Fug und Recht behaupten, dass dies die unterste Grenze aller Fehlerberechnungen bei der Anomalienbildung der globalen Mitteltemperatur sein muss. Ein Fehler von ± 0,46 °C kann deshalb in keinem Fall unterschritten werden. Bei einer Veränderung der globalen Temperaturanomalie von behaupteten 0,7 bis 0,8 ° C im vorigen Jahrhundert, verschwindet diese deshalb im Rauschen bzw. im breiten Unsicherheitsband.
Wird fortgesetzt.
Michael Limburg EIKE
[1] lt UNFCC der rechtlich bindenden Rahmenkonvention der UN von 1992, die Grundlage der IPCC Arbeit und den rechtlichen Rahmen für alle verbindlich setzend ist das Wort „Klimawandel“ (Climate Change) immer als mensch-gemacht zu verstehen und zu verwenden. Natürlicher Klimawandel muss hingegen als „Klimavariation“ (Climate variation) bezeichnet werden.
[2] Education is BS and MS in Chemistry from San Francisco State University. The Masters Degree research was in Physical Organic Chemistry. My Ph.D. is in Chemistry from Stanford University. After that I was a Bergman Postdoctoral Fellow at the Weizmann Institute of Science in Israel. The PhD and postdoctoral research involved Inorganic Biochemistry. This subject includes using physical and chemical methods to investigate the spectroscopy and chemistry of metalloproteins and metalloenzymes. These are proteins and enzymes that contain transition metals such as iron and copper.
For the last many years I have been a member of the research staff of the Stanford Synchrotron Radiation Lightsource, which is part of the SLAC National Accelerator Laboratory. There I use x-ray absorption spectroscopy to study the heavier elements found in biological systems; elements such as sulfur, vanadium, iron and copper. Some of my more recent research includes work with collaborators from France, Sweden, and Italy.
[3] Energy & Environment · Vol. 21, No. 8, 2010; Pat Frank; Uncertainty in the global average surface air temperature index: representative lower limit
[4] Energy & Environment · Energy & Environment · Vol. 22, No. 4, 2011; Pat Frank „Imposed and Neglected Uncertainty in the Global Average Surface 409 Air Temperature Index“[4]
[5] Brohan, P., Kennedy, J.J., Harris, I., Tett, S.F.B. and Jones, P.D., Uncertainty estimates in regional and global observed temperature changes: A new data set from 1850, J. Geophys. Res., 2006, 111 D12106 1-21; doi:10.1029/2005JD006548; see http://www.cru.uea.ac.uk/cru/info/warming/.
[6] Vertrauensbereich heißt, dass bei 1 σ 68,3 % der Messwerte innerhalb dieses Bandes liegen
[7] Diese Herleitung wird im 2. Paper von 2011 ausführlich behandelt
[8] Rauschverminderungstechniken bedeuten nichts anderes als Fehlerverminderungstechniken zufälliger Fehler
[9] Lin, X. and Hubbard, K.G., Sensor and Electronic Biases/Errors in Air Temperature Measurements in Common Weather Station Networks, J. Atmos. Ocean. Technol., 2004, 21 1025-1032.