Ich habe diesen Beitrag schon viele Male geschrieben. Ich versuche es nochmals. Mit den Ergebnissen meiner früheren Arbeiten war ich nicht zufrieden. Den Titel habe ich nach der 1954 erschienenen gleichnamigen Science Fiction Story gewählt, die ich mit zehn oder elf Jahren gelesen habe. Der Inhalt ist etwa Folgender:
Ein Mädchen reist als blinder Passagier an Bord eines Rettungsschiffes, um eine bestimmte Arznei zu irgendwelchen planetarischen Kolonisten zu bringen. Sie wird entdeckt, sobald das Mutterschiff weg ist. Unglücklicherweise ergeben die kalten Gleichungen, dass das Rettungsschiff nicht genügend Treibstoff hat, um mit ihrem zusätzlichen Gewicht an Bord zu landen; aber wenn sie die Arznei über Bord werfen, um das Schiff zu erleichtern, würde die ganze Kolonie sterben… also musste das Mädchen durch die Luftschleuse katapultiert werden, um im All zu sterben.
Ich war höchst beeindruckt von dieser Geschichte. Ich mochte Mathematik schon immer, und hier habe ich zum ersten Mal gesehen, wie Gleichungen uns mit unbestreitbaren und unumstößlichen Ergebnissen versorgen können. Und ich sah, dass diese Gleichungen über den zur Verfügung stehenden Treibstoff und das Gewicht in keiner Weise von menschlichen Emotionen beeinflusst waren; entweder waren sie richtig oder falsch, ganz gleich, welche Gefühle ich oder irgendjemand sonst dabei hatte.
Vor kurzem habe ich mir die Gleichungen der AGW-Wissenschaftler angesehen, die sie in ihren Modellen benutzen. Abbildung 1 zeigt die fundamentalste Klimagleichung, die fast immer stimmt:

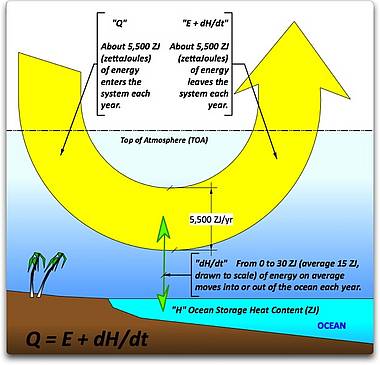
Abbildung 1. Die grundlegendste Klimagleichung besagt, dass die einfallende Energie gleich der ausgestrahlten Energie plus der in den Ozean gehenden Energie ist. Q ist die Menge der Energie, die in das System in einem bestimmten Zeitraum eingestrahlt wird. dH/dt ist die Veränderung der Wärmespeicherung in den Ozeanen von Anfang bis Ende dieses Zeitraumes. Die Einheit ist in allen Fällen Zettajoules (ZJ, oder 1021 Joule) pro Jahr.
Dies ist die gleiche Beziehung wie in der Wirtschaft, wo das, was ich innerhalb eines Jahres mache (in unserem Beispiel Q), gleich ist damit, was ich in jenem Jahr ausgebe plus die Änderungen meiner Ersparnisse von Jahr zu Jahr (dH/dt).
Jedoch, von hier starten wir in unbekannte Gewässer…
Ich werde meinen Text nehmen aus HEAT CAPACITY, TIME CONSTANT, AND SENSITIVITY OF EARTH’S CLIMATE SYSTEM , Stephen E. Schwartz, Juni 2007 (im Folgenden als S2007 bezeichnet). Die Studie ist weithin akzeptiert und wurde 49 mal in drei kurzen Jahren zitiert. Die Studie besagt unter Anderem Folgendes (Hervorhebung im Original):
Das Klimasystem der Erde enthält eine sehr empfindliche Balance zwischen der absorbierten kurzwelligen (solaren) Strahlung Q und der langwelligen Ausstrahlung (im thermischen Infrarot) an der Obergrenze der Atmosphäre E.
Q "fast gleich" E * (1)
Die globale und jährliche mittlere absorbierte kurzwellige Strahlung Q = gamma*J, wobei gamma für die mittlere planetarische Ko-Albedo (Komplement der Albedo) steht und J für die mittlere solare Strahlung an der Obergrenze der Atmosphäre (¼ der Solarkonstante) fast gleich 343 W/m2. Satellitenmessungen ergeben einen Wert Q fast gleich 237 W/m2 (Ramanthan 1987; Kiehl und Trenberth 1997), womit sich ein gamma von 0,69 ergibt. Die globale und jährliche mittlere langwellige Ausstrahlung kann mit der globalen und jährlichen mittleren Oberflächentemperatur GMST Ts in Beziehung gesetzt werden: E = epsilon x sigma x Ts^4, wobei epsilon für das effektive langwellige planetarische Emissionsvermögen (effective planetary longwave emissivity) steht, das definiert ist als das Verhältnis zwischen der globalen mittleren langwelligen Strahlung (flux), emittiert an der Obergrenze der Atmosphäre und jener durch die Stefan-Boltzmann-Gleichung berechnete der globalen mittleren Oberflächentemperatur; sigma ist die Stefan-Boltzmann-Konstante.
Innerhalb dieses Einschichten-Energiebilanzmodells (North et al. 1981; Dickinson, 1982; Hansen et al., 1985; Harvey, 2000; Andreae et al., 2005, Boer et al., 2007) führt ein Ungleichgewicht Q – E durch eine einfache Störung in Q oder E zu einer Änderungsrate des globalen Wärmegehalts, die beschrieben wird durch
dH/dt = Q – E (2)
wobei dH/dt für die Änderung des Wärmegehalts des Klimasystems steht.
Hmmm… Ich werde immer nervös, wenn jemand versucht, eine nicht nummerierte Gleichung in eine Studie einzuführen… aber ich schweife ab. Ihre Gleichung (2) ist die gleiche wie in meiner Abbildung 1 oben. Dies war ermutigend, weil ich die Abbildung 1 erstellt habe, bevor ich S2007 gelesen habe. In S2007 heißt es weiter (Hervorhebung von mir):
Der Ansatz des Energiebilanzmodells ist, dass dH/dt mit der Änderung der GMST (globale mittlere Oberflächentemperatur) in Beziehung stehen könnte, und zwar so:
dH/dt = C dTs/dt (3)
Hier steht C für die entsprechende Wärmekapazität. Es muss hier betont werden, dass C eine effektive Wärmekapazität ist, die nur den Teil der globalen Wärmekapazität reflektiert, der an die Störung im Zeitmaßstab der Störung gekoppelt ist [?]. Im gegenwärtigen Zusammenhang, der durch Änderungen der atmosphärischen Gasmischung im Zeitscale von Jahrzehnten und Jahrhunderten induzierten globalen Klimaänderung ist es das, was Gegenstand der Änderung in solchen Zeitscalen ist. Messungen des Wärmegehalts in den Ozeanen während der letzten 50 Jahre deuten darauf hin, dass diese Wärmekapazität von den oberen Schichten der Weltmeere dominiert wird.
[Im Original lautet dieser Absatz: „where C is the pertinent heat capacity. Here it must be stressed that C is an effective heat capacity that reflects only that portion of the global heat capacity that is coupled to the perturbation on the time scale of the perturbation. In the present context of global climate change induced by changes in atmospheric composition on the decade to century time scale the pertinent heat capacity is that which is subject to change in heat content on such time scales. Measurements of ocean heat content over the past 50 years indicate that this heat capacity is dominated by the heat capacity of the upper layers of the world ocean (Levitus et al., 2005).
Mit anderen Worten (unter Vernachlässigung der Ko-Albedo), sie schlagen zwei Einsetzungen in die Gleichung der Abbildung 1 vor. Sie sagen, dass
E = epsilon x sigma x Ts^4
und dass
dH/dt = C dTs/dt
was zu den Ergebnis führt
Q = epsilon x sigma x Ts^4 + C dTs/dt (4)
Abbildung 2 zeigt diese beiden Einsetzungen:

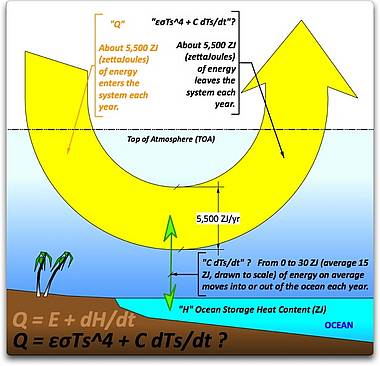
Abbildung 2. Eine graphische Darstellung der beiden zugrunde gelegten Einsetzungen in das „einschichtige Energiebilanzmodell“ der theoretischen Klimaerklärung. Die Originalgleichung vor der Einsetzung steht in hellbraun links unten, mit der Gleichung nach der Substitution darunter.
Warum sind diese Substitutionen wichtig? Man beachte, dass es in der Gleichung (4), wie in Abbildung 2 gezeigt, nur zwei Variablen gibt – Strahlung und Oberflächentemperatur. Sollten ihre Substitutionen gültig sein, bedeutet das, dass ein Strahlungsungleichgewicht nur durch eine Temperaturzunahme ausgeglichen wird. Oder wie es Dr. Andrew Lacis von NASA GISS ausdrückt (Hervorhebung von mir):

„Wie ich schon früher gesagt habe, die globale Erwärmung ist in der Physik ein Problem von Ursache und Wirkung, dass stark auf akkuraten Messungen und wohlbekannten physikalischen Prozessen basiert. Im Besonderen ist das Klima der Erde das Ergebnis der Energiebilanz zwischen einfallender Solarstrahlung und thermischer Ausstrahlung, gemessen an der Obergrenze der Atmosphäre, also strikt ein Problem der Strahlungsenergiebalance. Da der Strahlungsfluss ein wohlbekannter und gut verstandener physikalischer Prozess ist, haben wir genaue Kenntnisse darüber, was mit der globalen Energiebalance der Erde passiert. Und wie ich früher schon bemerkte, die Konservierung von Energie lässt als Reaktion auf das zunehmende atmosphärische CO2 zum Erreichen des globalen Gleichgewichts der Temperatur nichts anderes als eine Erwärmung zu.

Die Kommentare von Dr. Lacis sind nichts anderes al seine englischsprachige Erklärung der Gleichung (4) aus S2007. Wenn Gleichung (4) falsch ist, ist auch seine Behauptung falsch. Und seine Behauptung, dass die zunehmende Konzentration von Treibhausgasen nur durch einen Temperaturanstieg kompensiert werden kann, steht im Zentrum der AGW-Klimawissenschaft.
Außerdem gibt es noch einen zweiten Grund, warum ihre Substitutionen wichtig sind. In der Originalgleichung gibt es drei Variable – Q, E und H. Aber da es in der Version in S2007 nur zwei Variable gibt (Ts und Q), kann man die eine Gleichung mit den Termen der anderen lösen. Dies gestattet es ihnen, die Entwicklung der Oberflächentemperatur zu berechnen, mit gegebenen Schätzungen von Antriebskräften in der Zukunft… oder, in anderen Worten, das zukünftige Klima zu modellieren.
Da ich nun von Natur au seiner bin, der immer misstrauisch ist, war ich sehr neugierig über diese beiden Substitutionen. Dies vor allem deshalb, weil ihr gesamtes Kartenhaus in sich zusammenfallen würde, falls nur eine der beiden Substitutionen falsch ist. Ihre Behauptung, dass ein Ungleichgewicht der Strahlung nur durch zunehmende Temperatur ausgeglichen wird, kann so nicht stehen bleiben, wenn nicht beide Substitutionen gültig sind.
SUBSTITUTION 1
Lassen Sie mich beginnen mit der Substitution, die in Gleichung (3) beschrieben wird:
dH/dt = C dTs/dt (3)
Das erste, was mir auffiel, waren die Worte „der Ansatz des Energiebilanzmodells“ [Im Original steht wirklich das deutsche Wort ‚ Ansatz’.]
Und was”, sagte ich, „ist ein ‚Ansatz’, wenn er zu hause ist?” Ich war ursprünglich ein Cowboy, der sich selbst gebildet hat, das ist wahr, aber ein sehr belesener und reformierter Cowboy. Und ich habe nie etwas von einem ‚Ansatz’ gehört.
Also schaute ich im Internet bei Wolframs Mathe-Welt, die beste Quelle für Mathematik, und fand dies:
Ansatz

Ein Ansatz ist eine angenommene Formel für eine mathematische Feststellung, die nicht auf irgendeinem zugrunde liegenden Prinzip oder einer Theorie basiert.

Nun, das sollte Ihnen ein warmes, sicheres Gefühl geben. Diese kritische Gleichung, diese Substitution durch die Temperaturänderung als Proxie der Änderung im Wärmegehalt der Ozeane, auf der die gesamte Multimilliarden schwere Behauptung basiert, dass eine zunehmende Konzentration von Treibhausgasen unvermeidlich und unerbittlich zu einem Temperaturanstieg führt, wird von enthusiastischen AGW-Anhängern als „nicht basierend auf irgendeine zugrunde liegende Theorie oder ein Prinzip“ beschrieben. Man erinnere sich, wenn nur eine Substitution falsch ist, ist auch die ganze „wenn-sich-der-Antrieb-durch-Treibhausgase-ändert-folgt-dem-die-Temperatur“ – Behauptung hinfällig… und dafür bieten sie nicht einmal eine Rechtfertigung oder einen Bezug an, es ist lediglich ein Ansatz.
Das ist gut zu wissen und hätte eine viel weiter verbreitete Bekanntmachung verdient…
Dies erinnert mich an einen alten Witz: „Wie viele Beine hat eine Kuh, wenn man den Schwanz ein Bein nennt?“
…
„Vier, weil ein Schwanz kein Bein ist, auch wenn man ihn so nennt.“
Genauso: Wenn man die Änderung des Wärmegehalts der Ozeane eine lineare Transformation der Änderung der Oberflächentemperatur (C dTs/dt) nennt, heißt das noch lange nicht, dass das auch so ist.
Tatsächlich ist die Korrelation zwischen der jährlichen dH/dt und dTs/dt nicht statistisch signifikant (r^2=0.04, p=0.13). Zusätzlich sind die Verteilungen von dH/dt und dTs/dt ziemlich unterschiedlich, sowohl im vierteljährlichen als auch im jährlichen Niveau. In den Anhängen 1 und 4 findet man Details. Das bedeutet: nein, wir haben keinerlei beobachtete Beweise, dass ihre Substitution gültig ist. Viel eher ist das Gegenteil richtig, es gibt kaum eine Korrelation zwischen dH/dt und dTs/dt.
Es gibt noch ein drittes und subtileres Problem, wenn man dH/dt und dTs/dt miteinander vergleicht. Es besteht darin, dass H (der Wärmegehalt der Ozeane) etwas ganz anderes ist als die anderen drei Variablen, als da wären Q (Einstrahlung), E (Ausstrahlung) und Ts (globale mittlere Lufttemperatur am Boden). Der Unterschied besteht darin, dass H eine Quantität ist, während es sich bei Q, E und Ts um Strahlungsflüsse handelt.
Da Ts ein Fluss ist, kann es von der Einheit Kelvin (oder Grad Celsius) zu den Einheiten Watt pro Quadratmeter (W/m2) umgerechnet werden, und zwar unter Verwendung der Schwarzkörperbeziehung sigma x Ts^4.
Und da die zeitliche Ableitung der festen Größe H ein Fluss ist, nämlich dH/dt, kann man (zum Beispiel) E + dH/dt mit Q vergleichen, siehe Abbildung 1. Das kann man machen, weil wir Flüsse mit Flüssen vergleichen. Aber sie wollen einen Fluss (dH/dt) durch eine Änderung eines Flusses (dT/dt) ersetzen. Dies ist jedoch nur unter speziellen Umständen möglich.
Die Änderung des Wärmegehalts kann in einer einzigen speziellen Situation in Relation zur Temperaturänderung gesetzt werden. Und zwar wenn durch eine Temperaturdifferenz zwischen dem Objekt und der umgebenden Luft etwas erwärmt oder gekühlt wird. Zum Beispiel, wenn man etwas in den Kühlschrank legt, kühlt es sich durch den Unterschied der Temperatur zwischen dem Objekt und der Luft im Kühlschrank ab. Irgendwann hat das Objekt im Kühlschrank die allgemein dort herrschende Temperatur angenommen. Ergebnis: Die Temperaturänderung des Objektes ist eine Funktion des Temperaturunterschieds zwischen dem Objekt und der umgebenden Luft. Falls sich die Lufttemperatur im Kühlschrank ändert, hängt in diesem Fall dH/dt mit dT/dt zusammen.
Aber gilt das auch für unsere Situation? Wer der Meinung ist, dass, ähnlich wie im Kühlschrank, die Lufttemperatur über dem Ozean der Treiber des Wärmegehalts der Ozeane ist, der hebe die Hand… weil ich das mit Sicherheit nicht glaube. Ich glaube, dass es zu 100% umgekehrt ist. Allerdings scheint Schwartz das zu glauben, wenn er in einer Diskussion über die Zeitkonstante sagt:

„…wenn C die Wärmekapazität der Ozeane ist, dann ist dH/dt die Rate, mit der der Wärmegehalt in diesem Reservoir zunimmt, und ?T ist die Temperaturzunahme, die diesen Transfer antreibt.“

Zusätzlich zu dem Umstand, dass es sehr unwahrscheinlich ist, dass Änderungen der Lufttemperatur zu Änderungen des Wärmegehalts der Ozeane führen, spricht auch der Umfang der Änderung dieses Wärmegehaltes dagegen. Von 1955 bis 2005 änderte sich der Wärmegehalt der Ozeane um etwa 90 Zettajoule. Eine gleich große Änderung um 90 Zettajoule ereignete sich aber auch von einem Vierteljahr zum nächsten im Jahre 1983… Daher erscheint der Gedanke, dass Temperaturänderungen (dT/dt) die Änderungen des Wärmegehalts der Ozeane antreiben (und damit begrenzen) als sehr unwahrscheinlich.

Übersetzt und mit einer Einführung versehen von Chris Frey für EIKE
Im Original folgen noch vier Anhänge, die das hier Gesagte noch näher ausführen. Zusätzliche Aspekte stehen dort jedoch nicht, daher werden diese Anhänge hier aus Zeitgründen nicht mit übersetzt. Man bedenke, dass ich zusätzlich zu diesen ehrenamtlichen Übersetzungen einen Vollzeitjob habe und außerdem auch anderweitig noch ehrenamtlich engagiert bin, nämlich in der Kinderbetreuung.
C. F.
* Das "fast gleich" Zeichen (Doppelwelle), dass im Original steht, bildet dieser Editor nicht ab