GISS-Eskapaden; die merkwürdigen Statistiktricks des US Klimainstitutes GISS
Angeregt durch diesen Web-Beitrag über das Fehlen von Daten im Polarmeer, habe ich nachgeschaut, wie das GISS Daten erzeugt, wenn es gar keine gibt.
Das GISS ist das Goddard Institute for Space Studies und gehört zur NASA. Der Direktor des GISS ist Dr. James Hansen. Dr. Hansen ist ein unbefangener Wissenschaftler, der meint, man müsse Menschen, die nicht an seine apokalyptischen Visionen der Zukunft glauben, wegen „Hochverrats an der Menschlichkeit“ vor Gericht stellen. Das GISS erzeugt die GISTEMP genannte Historie der Erdoberflächentemperaturen. Hier ist seine Historie der Temperatur-Anomalie für Dez-Jan-Feb 2010 :
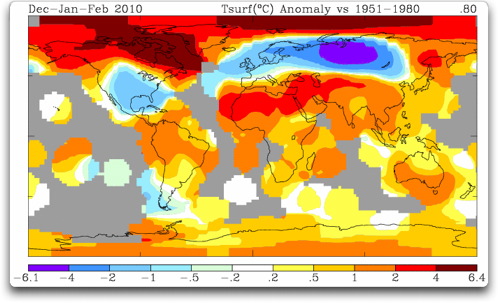
Abb. 1. GISS Temperatur-Anomalien DJF 2010. Für graue Gebiete gibt es keine Temperaturdaten.
Was stimmt mit dieser Darstellung nicht?
Das Kuriose an dieser Darstellung ist, daß uns Temperaturdaten geliefert werden, wo gar keine existieren. Vom Polarmeer haben wir zum Beispiel sehr wenig Messungen. Dennoch zeigt die GISS-Karte radikale Erwärmung im Polarmeer. Wie kommt das zustande?
Das Verfahren ist in einem Papier von 1987 von Hansen und Lebedeff skizziert. In jenem Papier schreiben sie, dass die jährlichen Temperaturänderungen über weite Strecken wohlkorreliert sind, über bis zu 1200 Km.
Aufgrund der von Hansen und Lebedeff entdeckten guten Korrelation (+0.5 und mehr) bis zu 1200 km von einer gegebenen Messstation, zeigt GISS die vermuteten Temperaturtrends innerhalb 1200 km von den Küstenstationen und 1200 km von den Stationen auf den Inseln. Gebiete außerhalb sind in grau dargestellt. Mit diesem 1200 km Radius können sie den “Temperaturtrend” des gesamten Polarmeers zeigen, wie in Abb. 1 dargestellt. Damit ist das Problem der sehr geringen Abdeckung im Polarmeer erledigt. Hier ist ein kleiner Teil des Problems dargestellt, die Abdeckung der Fläche nördlich 80° Nord:
(„Korrelation“ ist ein mathematisches Maß für die Ähnlichkeit zweier Datenbestände. Sie rangiert von „null“, d. h. keine Ähnlichkeit, bis plus oder minus “eins”, d. h. völlig gleich. Ein negatives Vorzeichen bedeutet Gleichheit, aber wenn der Wert eines Datenbestandes nach oben geht, nimmt der andere ab.)
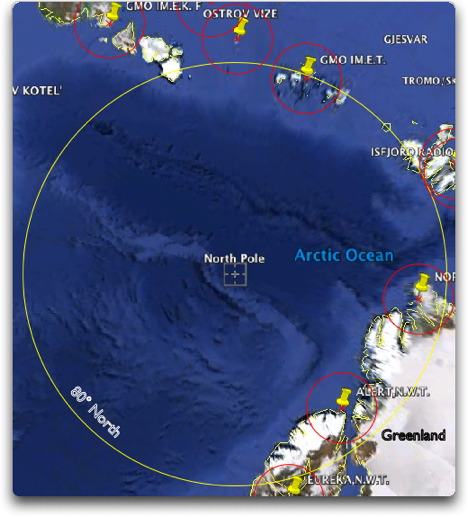
Abb. 2. Temperaturmessstationen bei 80° nördlicher Breite. Die Kreise um die Stationen haben 250 km Durchmesser. Man beachte, dass der Kreis bei 80°N einen Radius von etwa 1200 km hat, eine Größe, innerrhalb derer wir laut Hansen Temperaturtrends extrapolieren können.
Können wir wirklich annehmen, dass eine einzelne Station für ein derart großes Gebiet repräsentativ sein könnte? Sehen Sie sich Abb. 1 an, dort sind Trends angegeben für das gesamte Polarmeer, obschon es keine Messdaten gibt. Hier ist eine größere Ansicht, die das gesamte Polarmeer zeigt.
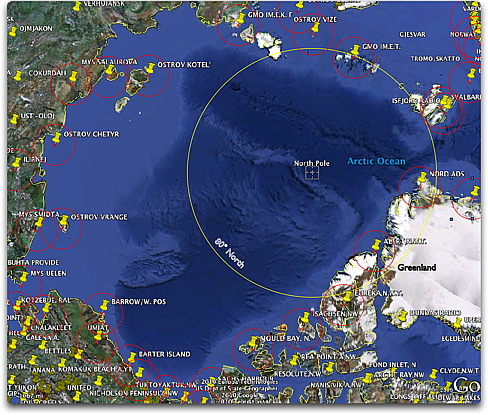
Abb. 3. Temperatur-Messstationen um das Polarmeer herum. Die Kreise um die Stationen haben etwa 250 km Durchmesser. Man beachte, dass die Fläche nördlich von of 80°N (gelber Kreis) etwa die dreifache Größe von Alaska hat.
Was die Dres. Hansen und Lebedeff 1987 nicht bemerkten, und niemand scheint es seither bemerkt zu haben, ist, dass ihre Erkenntnisse in Bezug auf die Korrelation von weit entfernten Messstationen sehr problematisch sind. Das zeigt die folgende Graphik.
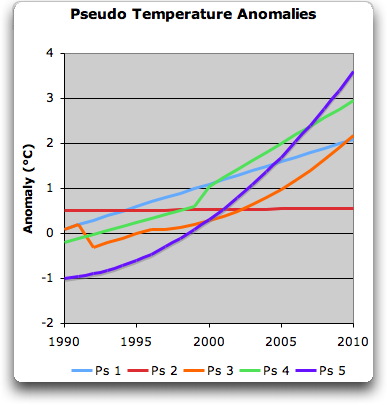
Abb. 4. Fünf Pseudo-Temperatur-Historien. Man beachte die Unterschiede in der Form der Historien und in den Trends.
Merkwürdigerweise gleichen sich diese Pseudo-Temperatur-Historien trotz ihren offensichtlichen Unterschieden in einem, der Korrelation. Die Korrelation zwischen jeder einzelnen Pseudo-Temperatur-Historie und den anderen Pseudo-Temperatur-Historien ist größer 90%.
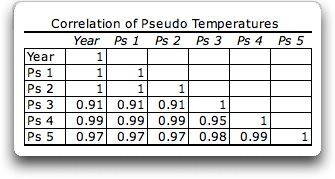
Abb. 5. Korrelation zwischen den Pseudo-Temperatur-Historien aus Abb. 3.
Die unausweichliche Folgerung daraus ist, dass hohe Korrelationswerte zwischen Temperatur-Historien nicht bedeuten, dass deren Trends sich ähneln.
In Ordnung, ich kann schon hören, was Sie denken: „Ja, stimmt, für einige imaginäre kurze 20-jährige Pseudo-Temperatur-Historien kann man einige wilde Daten finden, die unterschiedliche Trends aufweisen. Doch was ist mit den realen 50-jährigen Temperatur-Historien, wie sie Hansen und Lebedeff benutzten?“
Gut, dass diese Frage kommt … hier sind neunzehn 50-jährige Temperatur-Historien von Alaska. Alle korrelieren mit Anchorage höher als 0,5 (max 0.94, min 0.51, Durchschnitt 0.75).
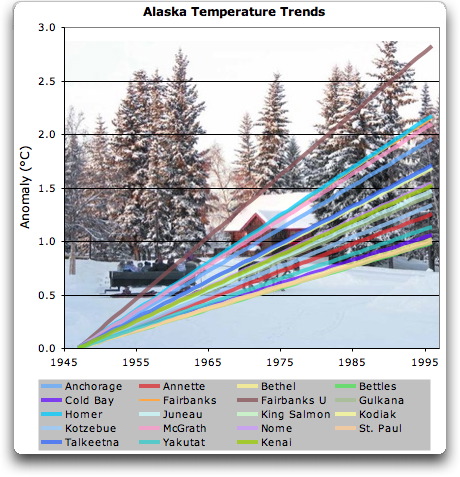
Abb. 6. Trends von Temperatur-Historien von Alaska-MessStationen. Foto stammt aus Pioneer Park, Fairbanks.
Man sieht, die Trends rangieren von etwa einem Grad in 50 Jahren bis nahe drei Grad. Trotz dieser riesigen Spannweite (ca. 300%) bei den Trends haben alle eine gute Korrelation (größer +0,5) mit Anchorage. Das zeigt klar, dass eine gute Korrelation zwischen den Temperatur-Historien nichts aussagt über deren korrespondierende Trends.
Und schließlich ist meines Wissens dieses Extrapolationsverfahren von Hansen und dem GISTEMP einmalig. Es wird von keinem anderen Erzeuger von globalen oder regionalen Datenhistorien benutzt, wie z. B. vom CRU oder USHCN. Wie Kevin Trenberth in den CRU-Emails über die Diskrepanz zwischen GISTEMP und den anderen Datenhistorien sagte (Hervorhebung durch den Verf.):
Nach meinem Verständnis ist die größte Quelle dieser Diskrepanz [zwischen globalen Datenhistorien] die Art und Weise, wie die Arktis analysiert wird. Wir wissen, dass das Meereis auf Rekordniedrigständen war, 22% weniger als im vorhergehenden Niedrigjahr 2005. Einige Meer- und Lufttemperaturen waren bis zu 7C höher als Normal. Aber meistens gibt es keine konventionell ermittelten Daten. Bei der NASA [GISTEMP] extrapoliert man und baut die hohen Temperaturen in der Arktis ein. In anderen Datenreihen tut man das nicht. Nur verfügbaren Daten werden benutzt, das Übrige fehlt.
Keine Daten verfügbar? Kein Problem, baue einfach einige hohe Temperaturen ein
Was ergibt sich daraus?
Hansen und Lebedeff lagen richtig damit, dass die jährlichen Temperatur-Historien von weit auseinander liegenden Messstationen dazu neigen, gut korreliert zu sein. Allerdings lagen sie nicht richtig mit ihrer Meinung, dass dies für die Trends der gut korrelierten Temperatur-Historien gälte. Deren Trends können völlig ungleich sein. Im Ergebnis ist die Extrapolation von Trends aus einer bis zu 1200 km entfernten Messstation ein unzulässiges Verfahren ohne jegliche mathematische Basis.
[Nachfolgend zwei Berichtigungen aus dem Kommentarbereich der Originalquelle]
[Aktualisierung 1] Fred N. merkte an, dass GISS eine polare Sicht auf die gleichen Daten zeigt. Man beachte den Anspruch der Gültigkeit für das gesamte Polarmeer. Danke.
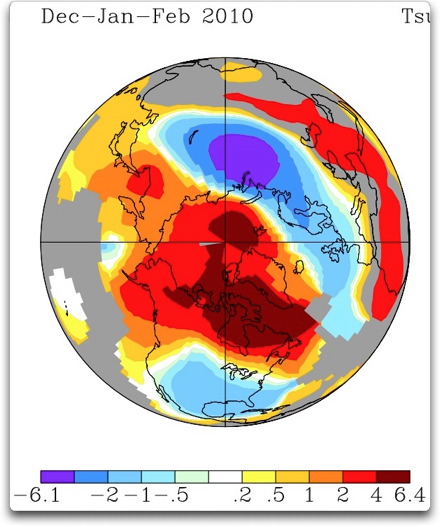
[Aktualisierung 2] JAE wies darauf hin, dass Abb. 1 keine Trends zeigt, sondern Anomalien. BOBALLAB verwies mich auf die Karte mit den tatsächlichen Trends. Beiden Lesern meinen Dank. Hier ist die zutreffende Darstellung:
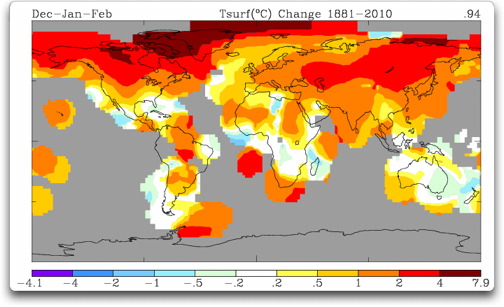
Erschienen am 25. 03. 2010 als Gastbeitrag von Willis Eschenbach auf der Watts Up Seite. Die Übersetzung besorgte dankenswerterweise Hellmut Jäger für EIKE